令和4年1月の1陸技の試験1回目の無線工学BのA-6~10の問題について解説します。
R.4.1 無線工学B(1回目) A-6
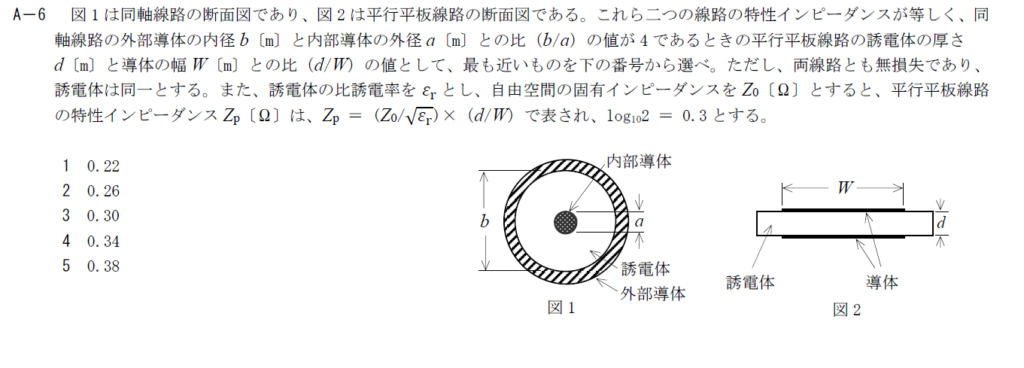
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-6
同軸線路と平行平板線路の特性インピーダンスに関する問題です。
平行平板線路のインピーダンスについては問題文中に記載されているので、実質的に同軸線路の特性インピーダンスを求める問題に帰着します。
同軸ケーブルの単位長さあたりのインダクタンス$L$と静電容量$C$は次のように表せます。
真面目に計算するとかなり大変なので別記事にまとめたいと思います。
\[
L=\frac{\mu_0}{2\pi}\log_e\frac{b}{a} =\frac{\mu_0}{2\pi\log_{10}e}\log_{10}\frac{b}{a} \\
C=\frac{2\pi \epsilon_0 \epsilon_r}{\log_e\frac{b}{a}} = \frac{2\pi \epsilon_0 \epsilon_r \log_{10}e}{\log_{10}\frac{b}{a}}
\]
2個目のイコールでは自然対数を常用対数に直しています。
自由空間の特性インピーダンス$Z_0=\sqrt{\frac{\mu_0}{\epsilon_0}}$を使って、特性インピーダンス$Z_c$は次のように表せます。
\[
Z_c=\sqrt{\frac{L}{C}}=\frac{Z_0}{2\pi \sqrt{\epsilon_r}\log_{10}e}\log_{10}\frac{b}{a}
\]
問題文から$b/a=4, Z_c=Z_p$なので、
\[
d/W=\frac{2\log_{10}2}{2\pi \log_{10}e}=0.219\simeq 0.22
\]
以上から
答えは1の0.22です。
この問題は下記の動画でも解説しています。
R.4.1 無線工学B(1回目) A-7

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-7
特性インピーダンス$Z_0$の給電線にインピーダンス$Z_R$の負荷を接続したときの電圧定在波比VSWRは次のように表されます。
\[
VSWR=\frac{|Z_R+Z_0|+|Z_R-Z_0|}{|Z_R+Z_0|-|Z_R-Z_0|}
\]
$Z_R>Z_0$と$Z_R< Z_0$の場合両方考えておきましょう。
$Z_R>Z_0$の時は
$VSWR=\frac{Z_R}{Z_0}$なので$Z_R=1.35 \times 75=101.25[\rm{\Omega}]$
$Z_R< Z_0$の時は
$VSWR=\frac{Z_0}{Z_R}$なので$Z_R=\frac{75}{1.35}=55.55 \simeq 55.6[\rm{\Omega}]$
以上から
答えは2の55.6[Ω]です。
この問題は下記の動画でも解説しています。
R.4.1 無線工学B(1回目) A-8

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-8
1/4波長整合回路に関する問題です。
A
線路のインピーダンスについて覚えていればそのまま答えが出せるでしょう。
ここでは真面目に求めてみます。
接続点Pの両端の電圧を$V$、流れる電流を$I$、負荷抵抗にかかる電圧を$V_r$、流れる電流を$I_r$とします。
正弦波を流すことを考えて、
\[
V=V_1e^{j\beta l}+V_2e^{-j\beta l} \\
I=\frac{1}{Z}(V_1e^{j\beta l}-V_2e^{-j\beta l})
\]
と表すことにしましょう。
給電線は無損失なので接続点P($l=0$)では$V=V_r, I=I_r$なので、
\[
V_1=(V_r+I_rZ)/2 \\
V_2=(V_r-I_rZ)/2
\]
となります。
これを$V, I$に代入して
\[
V=\frac{V_r+I_rZ}{2}e^{j\beta l}+\frac{V_r-I_rZ}{2}e^{-j\beta l}=V_r\cos \beta l +jI_rZ \sin \beta l \\
I=\frac{1}{Z}\left\{\frac{V_r+I_rZ}{2}e^{j\beta l}-\frac{V_r-I_rZ}{2}e^{-j\beta l}\right\} =I_r\cos \beta l +j\frac{V_r}{Z} \sin \beta l
\]
です。
\[
Z_X=V/I=Z \times \frac{R\cos \beta l +jZ \sin \beta l}{Z\cos \beta l +jR \sin \beta l}
\]
ここで、$R=V_r/I_r$を使っています。
以上から、
Aには$\frac{R\cos \beta l +jZ \sin \beta l}{Z\cos \beta l +jR \sin \beta l}$が入ります。
B
$l=\lambda /4$の時は
$\frac{2\pi}{\lambda}\frac{\lambda}{4}=\frac{\pi}{2}$です。
C
$\beta l=\pi/2$なので、代入すると
$Z_X=\frac{Z^2}{R}$となります。
D
整合が取れている時は$Z_X=Z_0$なので
$Z=\sqrt{Z_0R}$となります。
以上から
答えは4です。
R.4.1 無線工学B(1回目) A-9
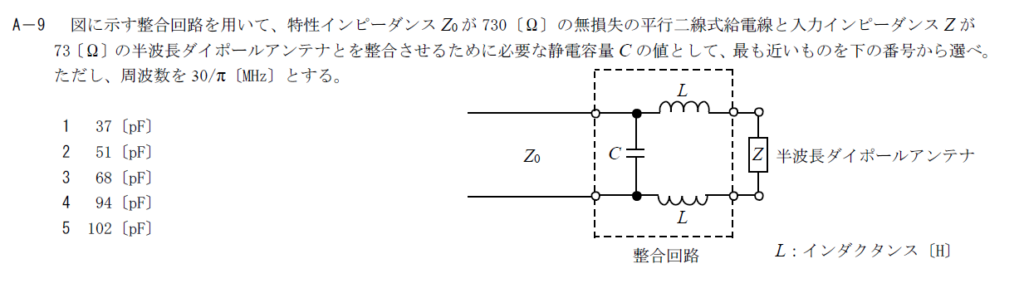
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-9
整合回路に関する問題です。
式を覚えていればすぐ解ける問題ですが、最悪導出できます。
ただし、恐ろしく面倒くさいので覚えておくか、ど忘れしてしまったら、一旦後回しにして余った時間で計算しましょう。
この形($Z_0 >Z$で平衡な給電線の場合)の整合条件は
\[
L=\frac{1}{2\omega}\sqrt{Z(Z_0-Z)} \\
C=\frac{1}{\omega Z_0}\sqrt{\frac{Z_0-Z}{Z}}
\]
です。
静電容量の式に代入すれば
\[
C=6.84 \times 10^{-11}[\rm{F}]\simeq 68[\rm{pF}]
\]
となります。
以上から、
答えは3「68[pF]」です。
この式は給電線から見たアンテナ側のインピーダンスが$Z_0$と等しいという関係から導出できます。
給電線から見ると「2つのLとアンテナの直列回路」と「コンデンサ」の並列回路なのでその合成インピーダンスを求めて、$Z_0$と等しいとします。
気になったら一度自分の手を動かして計算してみてください。
R.4.1 無線工学B(1回目) A-10

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-10
各種アンテナの特徴に関する問題です。
明らかな誤りが一つありますので即答してしまいましょう。
誤った選択肢は4です。
90°のコーナレフレクタは励振素子1つと鏡像アンテナ3個の合計4波の合成となります。
模式図を下記に示します。
丸が励振素子と同位相、バツが励振素子と逆位相の波源を示します。

開き角が90°のときの鏡像位置
以上から
答えは4です。
まとめ
今回は先日行われた令和4年1月1回目の1陸技の無線工学BのA-6~10を解いてみました。
先週受験した方はお疲れさまでした。
試験はいかがだったでしょうか?
これから受験される方も7月の試験に向けて計画的に準備していきましょう。
勉強法
第一級陸上無線技術士の勉強法とおすすめ参考書
参考文献
電磁気学をちゃんと学びたい人向け
リンク
上の難易度が高い人
リンク
リンク








コメント