【過去問解説】令和6年7月の1陸技試験問題を解いてみた（R6.7 無線工学B A-1~A-5）

令和6年1月の一陸技の試験の無線工学BのA-1～5の問題について解説します。

R.6.7 無線工学B A-1

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年7月　無線工学B A-1

平面波を波動方程式から導出する問題です。

この問題は同様の問題が令和4年7月1回目A-1で出題されています。 文章は全く同じで、Aの空欄の位置のみ異なります。

下記の記事をご参照ください。

【過去問解説】令和4年7月の1陸技試験問題を解いてみた（R4.7 1回目 無線工学B A-1~A-5）

１陸技令和4年7月の無線工学B(1回目)の問題を解いてみました。今回はA-1~5です。

jr2kcb.com

2022.07.23

A

Aに関してはMaxwell方程式のうちのFaradayの法則の両辺に$\vec{\nabla}\times$を取った結果を使って下記のようになります。

$$\{\vec{\nabla}^2-\frac{1}{c^2} \frac{\partial^2}{\partial t^2}\} \vec{E}=0$$ この式の導出は下記の記事に記載しています。

【資格】無線従事者のための物理学-電磁波の導出-

MathJax.Hub.Config({tex2jax: {inlineMath: , ]}});無線従事者をはじめとする技術関係の資格試験でいきなり覚えろと言わんばかりに公式などが出てきて困惑した経験はないでしょうか？私は理解しないと次に...

jr2kcb.com

2020.10.11

一方で問題文から電界$\vec{E}$は角周波数$\omega$で正弦波的に変化するので $$\vec{E}=\vec{E_0}e^{-j\omega t}$$ と書けます。

これを代入すると $$\vec{\nabla}^2\vec{E}+ \frac{\omega ^2}{c^2}\vec{E}=0$$ ここで$c=\frac{1}{\sqrt{\mu_0\epsilon_0}}$なので、 $$\vec{\nabla}^2\vec{E}+ k^2\vec{E}=0$$

となります。

そのため、Aには「$\nabla^2 \vec{E}$」が入ります。

他は過去問と一緒で \

• A:$\nabla^2 \vec{E}$
• B:前進波
• C:$\frac{1}{f\sqrt{\mu_0\epsilon_0}}$
• D:$\frac{1}{\sqrt{\mu_0\epsilon_0}}$

となり、答えは1です。

R.6.7 無線工学B A-2

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年7月　無線工学B A-2

直線状アンテナの放射抵抗を求める問題です。

この問題については同様の問題が令和4年1月2回目A-3で出題されています。 値が違うだけなので計算方法は下記をご参照ください。

【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 2回目 無線工学B A-1~A-5）

１陸技令和4年1月の無線工学B(2回目)の問題を解いてみました。今回はA-1~5です。

jr2kcb.com

2022.04.09

$$R=P/I^2=80\left(\frac{\pi l}{\lambda}\right)^2 \\ =80\times \left(\frac{\pi \times 1}{10}\right)^2=7.89 \simeq 7.9$$

以上から答えは4です。

R.6.7 無線工学B A-3

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年7月　無線工学B A-3

指向性利得を計算する問題です。 計算が面倒くさいので注意してください。

この問題は全く同じ問題が令和3年7月1回目A-2で出題されています。

下記の記事をご参照ください。

【過去問解説】令和3年7月の1陸技試験問題を解いてみた（R3.7 1回目　無線工学B A-1~A-5）

１陸技令和3年7月の無線工学Bの問題を解いてみました。今回は第1回A-1~5を解きました。

jr2kcb.com

2021.08.01

それぞれの半値幅をラジアンに直すと $$\theta_E=\frac{3.9\pi}{180}$$ $$\theta_H=\frac{5.2\pi}{180}$$ となります。

与えられた計算式に代入して $$G_d=\frac{4\pi}{\pi^2}\frac{180^2}{3.9\times 5.2}=2034 \simeq 2034$$ となるため、デシベルに直すと $$G_d\simeq 10\log_{10} 2000=33\rm{[dB]}$$ となり、答えア2です。

各選択肢は3dB(2倍)ずつ離れているので$\pi \simeq 3, 3.9 \pi \simeq 4, 5.2 \simeq 5$のように概算しても正解は出せます。

時間短縮のためにも程よい概算ができるように練習しておきましょう。

R.6.7 無線工学B A-4

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年7月　無線工学B A-4

開口面アンテナの基本的な性質に関して誤った選択肢を選ぶ問題です。

誤った選択肢は1です。

アンテナの開口効率の定義は$A_e/A$なので分母と分子が逆です。

一般に実効面積は開口面積より小さくなるので問題文の式だと1を超えることになります。

以上から、答えは1です。

R.6.7 無線工学B A-5

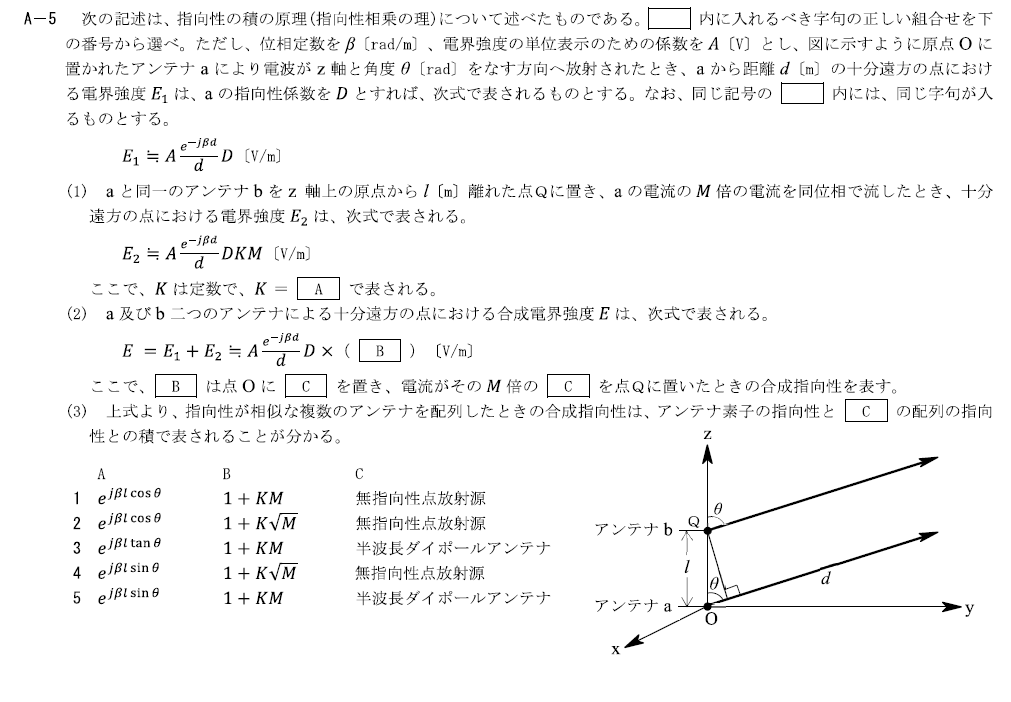
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年7月　無線工学B A-5

指向性の積の原理に関する問題です。

この問題は全く同じ問題が令和4年1月1回目A-2で出題されています。

下記の記事をご参照ください。

【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 無線工学B A-1~A-5）

１陸技令和4年1月の無線工学B(1回目)の問題を解いてみました。今回はA-1~5です。

jr2kcb.com

2022.01.29

答えは

• A:$e^{j\beta l\cos \theta}$
• B:$1+KM$
• C:無指向性点放射源

で1です。

まとめ

今回は令和6年7月の無線工学Bの試験A-1~A-5の問題について解説しました。 一陸技は過去問と類似または全く同じ問題が出題されやすい試験です。 計算が面倒くさいことも多いので早く簡単に求める方法を問題演習によって練習しておきましょう。 過去問を数年分解いておくだけでかなりの対策になります。

勉強法 第一級陸上無線技術士の勉強法とおすすめ参考書

参考文献

電磁気学をちゃんと学びたい人向け

上の難易度が高い人