【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 無線工学B A-11~A-15）

令和4年1月の1陸技の試験1回目の無線工学BのA-11～15の問題について解説します。

R.4.1 無線工学B（1回目） A-11

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月1回目　無線工学B A-11

折返し半波長ダイポールアンテナに関する問題です。

半波長ダイポールアンテナは折り返すとその分だけ実効長は増え、利得は変化しません。

三線式半波長ダイポールの場合はエレメントが3本あるので、実効長は半波長ダイポールの3倍になります。
半波長ダイポールアンテナの実効長は$\frac{\lambda}{\pi}$なので、
$$l_e=3\times \frac{\lambda}{\pi} =3 \times \frac{1}{\pi}\simeq 96[\rm{cm}]$$
です。

ちなみに、この問題の計算は真面目に計算する必要はありません。
$\pi$は3より少し大きいので、100[cm]に近い選択肢の内100[cm]より少し小さいものを選べば答えになります。
試験時間は限られているので簡単に答えが出せる時は簡略化して考えましょう。

以上から、答えは2の96[cm]です。

R.4.1 無線工学B（1回目） A-12

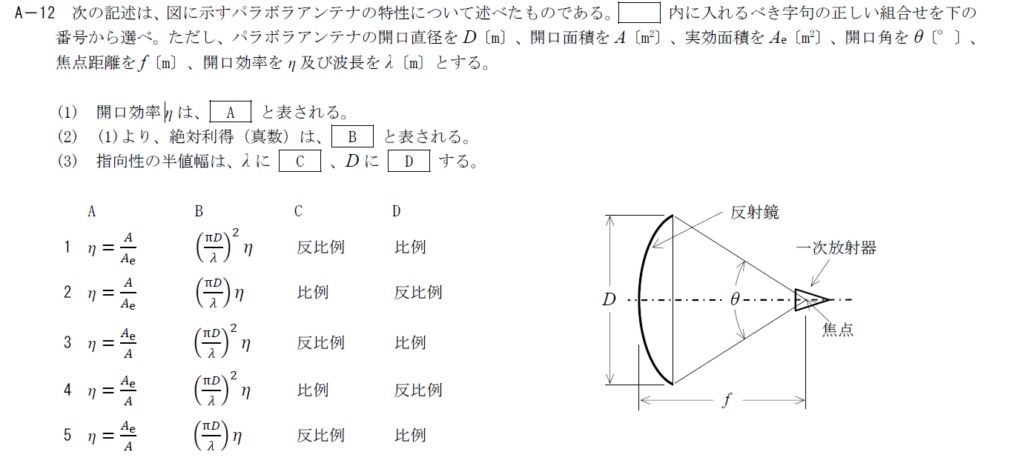
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月1回目　無線工学B A-12

パラボラアンテナに関する問題です。

A

開口効率は実際のアンテナの面積に対する、実効的面積の比を表すので$A_e/A$となります。

そのため、Aには$\eta =\frac{A_e}{A}$が入ります。

B

利得は
$$G=\frac{4\pi A_e}{\lambda ^2}=\frac{4\pi \eta A}{\lambda} =\frac{4\pi \eta}{\lambda}\frac{\pi D^2}{4}=\left( \frac{\pi D}{\lambda}\right)^2 \eta$$
と表せます。

そのため、Bには$\left( \frac{\pi D}{\lambda}\right)^2 \eta$が入ります。

C,D

CとDは指向性の半値幅に関する空欄です。

パラボラアンテナの半値幅は$\theta_{3dB} \simeq \frac{70\lambda}{D}\rm{[°]}$となります。

表式の中の70は60~70程度と言われています。
これはパラボラアンテナの特性上反射鏡からまっすぐ電波が飛ぶので、半値幅が狭いことを表す値で、おそらく実測から推定された値です。
直感的には波長が長いほど回折しやすいため半値幅は$\lambda$に比例し、反射鏡の面積が大きいほど一次放射器から放射される電波をより多く反射できるため$D$に反比例します。

そのため、Cには「比例」、Dには「反比例」が入ります。

以上から答えは4です。

R.4.1 無線工学B（1回目） A-13

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月1回目　無線工学B A-13

カセグレンアンテナに関する問題です。

カセグレンアンテナは一次放射器、回転双曲面の副反射鏡、回転放物面の主反射鏡から構成されるアンテナです。
難しい書き方をしていますが、カセグレンアンテナはパラボラアンテナの一次放射器を副反射鏡に変えたアンテナです。
こうすることで一次放射器を主反射鏡の中心に置くことができ、一次放射器への給電が楽になります。

選択肢の中で誤っているものは4です。

カセグレンアンテナでは副反射鏡やその支柱で電波が散乱されて放射特性に乱れが発生します。
オフセットカセグレンアンテナにすることで、主反射鏡で反射された電波の通り道に副反射鏡などがなくなるので、放射特性の乱れは少なくなります。

R.4.1 無線工学B（1回目） A-14

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月1回目　無線工学B A-14

直接波と大地反射波の干渉（いわゆる2波モデル）に関する問題です。

反射波の直接波に対する位相差を$\phi$、直接波の電界強度を$E_0$、反射波の電界強度を$E_r$とします。 大地の反射係数が-1なので$E_0=E_r$とみなせます。

受信点の電界強度$E$は$E=E_0|1-\exp (j\phi)|=2E_0|\sin (\phi/2)|$です。

次に位相差を求めましょう。

直接波と大地反射波の経路差は送信アンテナの地上高を$h_t$、受信店の地上高を$h_r$とすると
$$\sqrt{d^2+(h_t+h_r)^2}-\sqrt{d^2+(h_t^2-h_r)^2}=\frac{2h_th_r}{d}$$
となります。

そのため、位相差$\phi$は$\phi=\frac{4\pi h_t h_r}{\lambda d}$です。

$\frac{4\pi h_t h_r}{\lambda d} << 1$なので$E=2E_0 \frac{2\pi h_t h_r}{\lambda d}$と表せます。

問題文で与えられた値を代入すると$E=40\pi =126\rm{[\mu V/m]}$となります。

以上から、答えは5「$126\rm{[\mu V/m]}$」です。

R.4.1 無線工学B（1回目） A-15

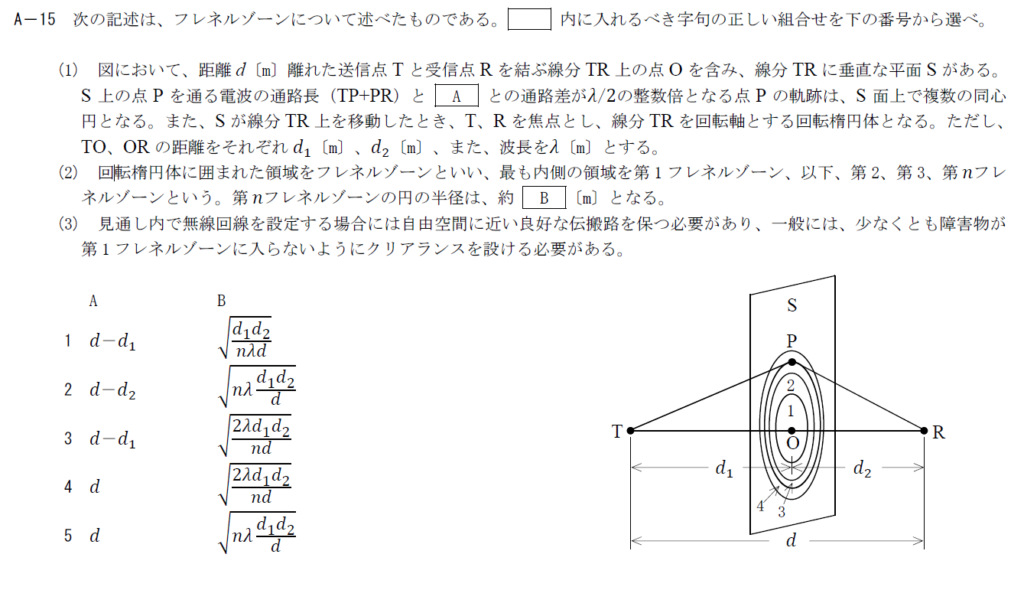
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月1回目　無線工学B A-15

フレネルゾーンに関する問題です。

フレネルゾーン内にナイフエッジ上の障害物が存在するとそれによる回折波と直接波が干渉します。

この問題ではフレネルゾーンの導出を行っています。

A

先程の説明通り、フレネルゾーンは直接波と回折波が干渉する領域なのでPを通る経路（回折波）とTRを直接伝搬する経路を考えることになります。
この経路長は$d$なので、Aには$d$が入ります。

B

第nフレネルゾーンでは経路差が$\lambda /2$のn倍となります。

実際に経路差を計算して、フレネルゾーンの半径を求めてみましょう。

第nフレネルゾーンの半径を$r$とします。
回折波の経路長は
$$(TP+PR)=\sqrt{d_1^2+r^2}+\sqrt{d_2^2+r^2}$$
です。

ここで、$d_1,d_2 >> r$としましょう。
波長に対して十分離れた送受信点を考えているので、それほどおかしな近似ではありません。
すると
$$(TP+PR)=d_1\left\{ 1+\frac{r^2}{2d_1^2}\right\}+d_2\left\{1+\frac{r^2}{2d_2^2}\right\}=d+\frac{r^2}{2d_1}+\frac{r^2}{2d_2}$$
となります。
2波の経路差$l$は$d$との経路差なので、
$$l=\frac{r^2}{2d_1}+\frac{r^2}{2d_2}$$
となります。

フレネルゾーンの条件から$l=\frac{n\lambda}{2}$なので、
$$\frac{r^2}{2d_1}+\frac{r^2}{2d_2}=\frac{n\lambda}{2}$$
です。
これを$r$について解くと
$$r=\sqrt{n\lambda \frac{d_1d_2}{d}}$$
となります。

そのため、Bには$\sqrt{n\lambda \frac{d_1d_2}{d}}$が入ります。

以上から答えは5です。

まとめ

先日行われた令和4年1月1回目の1陸技の無線工学BのA-11～15を解いてみました。
今回は式を覚えていれば解ける問題多いですが、忘れていても最悪その場で導出できます。
暗記だけでなく、要所要所を抑えた試験対策ができると良いですね。

勉強法

第一級陸上無線技術士の勉強法とおすすめ参考書

参考文献

電磁気学をちゃんと学びたい人向け

上の難易度が高い人