【過去問解説】令和6年7月の1陸技試験問題を解いてみた（R6.7 無線工学A A-6~A-10）

令和6年7月の一陸技の試験の無線工学AのA-6～10の問題について解説します。

R.6.7 無線工学A A-6
1. A
2. B
3. C
R.6.7 無線工学A A-7
R.6.7 無線工学A A-8
1. A
2. B,C
R.6.7 無線工学A A-9
1. A
2. B
3. C,D
R.6.7 無線工学A A-10
まとめ
参考文献

R.6.7 無線工学A A-6

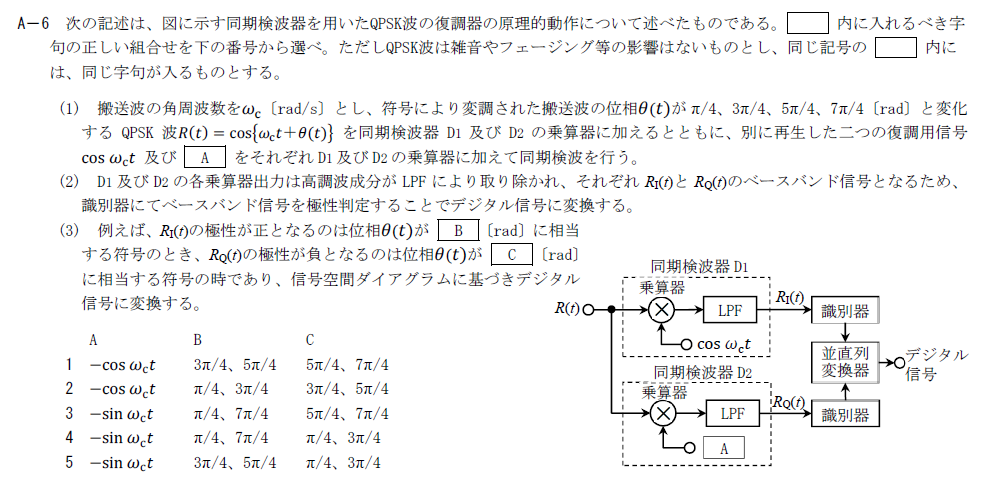
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年7月　無線工学A A-6

この問題は類似問題が令和5年1月2回目A-5で出題されています。

下記の記事もご参照ください。

【過去問解説】令和5年1月の1陸技試験問題を解いてみた（R5.1 2回目無線工学A A-1~A-5）

１陸技令和5年1月の無線工学A(2回目)の問題を解いてみました。今回はA-1~5です。

また位相の定義が違う問題として令和4年1月1回目A-5があります。

【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 無線工学A A-1~A-5）

１陸技令和4年1月の無線工学A(1回目)の問題を解いてみました。今回はA-1~5です。

A

2つの同期検波器ではそれぞれ直交する復調用信号をQPSK波に乗算します。

ここではD1で$\cos \omega_ct$を乗算しているのでAには「$-\sin \omega_ct$」が入ります。

B

D1の乗算器の出力は \[ \cos\left\{\omega_ct +\theta (t)\right\}\cos \omega_ct \\ =\frac{1}{2}\cos\left\{ 2\omega_ct +\theta (t)\right\}+\frac{1}{2}\cos \theta (t) \] なので、LPFを通すと$R_I(t)$は下記のようになります。 \[ R_I(t)=\frac{1}{2}\cos \theta (t) \]

$R_I(t)$が正になるのは \[ \theta (t)=\frac{\pi}{4},\frac{7}{4}\pi \] の時です。

そのため、Bには「$\frac{\pi}{4},\frac{7}{4}\pi$」が入ります。

C

Bと同様に計算してD2の乗算器の出力は \[ -\cos\left\{\omega_ct +\theta (t)\right\}\sin \omega_ct \\ =-\frac{1}{2}\sin\left\{ 2\omega_ct +\theta (t)\right\}+\frac{1}{2}\sin \theta (t) \] なので、LPFを通すと$R_I(t)$は下記のようになります。 \[ R_Q(t)=\frac{1}{2}\sin \theta (t) \]

$R_Q(t)$が負になるのは \[ \theta (t)=\frac{5}{4}\pi ,\frac{7}{4}\pi \] の時です。

そのため、Cには「$\frac{5}{4}\pi ,\frac{7}{4}\pi$」が入ります。

以上から答えは3です。

R.6.7 無線工学A A-7

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年7月　無線工学A A-7

周波数変調波のS/N改善係数を計算する問題です。

この問題については同様の問題が令和5年1月1回目A-7で出題されています。

数字が違うだけなので下記の記事をご参照ください。

【過去問解説】令和5年1月の1陸技試験問題を解いてみた（R5.1 1回目無線工学A A-6~A-10）

１陸技令和5年1月の無線工学A(1回目)の問題を解いてみました。今回はA-6~10です。

\[ f_d=mf_p=6\rm{[kHz]} \] なのでこの値を与えられた式に代入すると \[ I=10\log_{10}\left\{3f_d^2B/(2f_p^3)\right\} \\ =10\log_{10}20 \\ =13\rm{[dB]} \] となります。

以上から答えは2です。

R.6.7 無線工学A A-8

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年7月　無線工学A A-8

スーパーヘテロダイン受信機の相互変調と混変調に関する問題です。

この問題は同様の問題が令和4年7月2回目A-8で出題されています。 Aの空欄以外は全く同じです。

下記の記事もご参照ください。

【過去問解説】令和4年7月の1陸技試験問題を解いてみた（R4.7 2回目無線工学A A-6~A-10）

１陸技令和4年7月の無線工A(2回目)の問題を解いてみました。今回はA-6~10です。

A

問題文の$3f_1-2f_2$や$3f_2-2f_1$は5次の相互変調積の周波数成分です。

B,C

この2つの空欄は上記の記事と同じで

B:変調
C:$f_d \pm f_m$

です。

以上から答えは4です。

R.6.7 無線工学A A-9

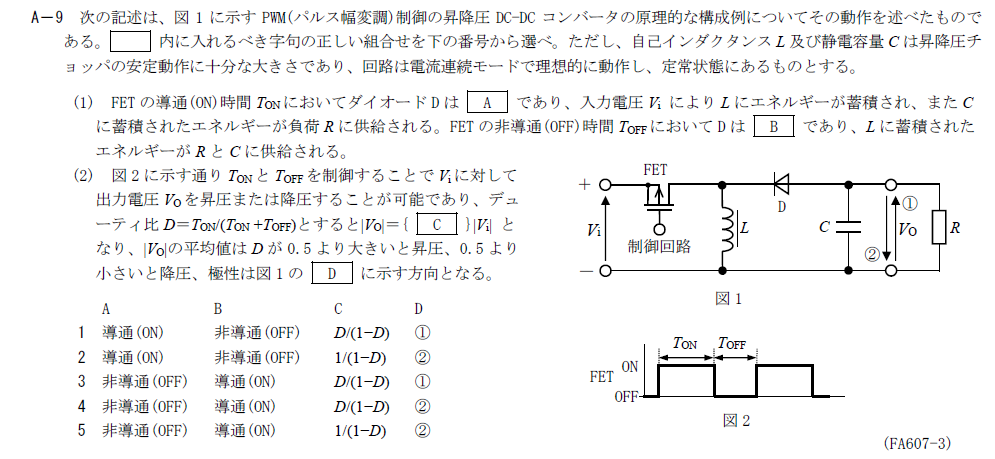
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年7月　無線工学A A-9

PWM制御の昇降圧DC-DCコンバータに関する問題です。

この問題は類似問題が令和4年1月1回目A-10で出題されています。

【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 無線工学A A-6~A-10）

１陸技令和4年1月の無線工学A(1回目)の問題を解いてみました。今回はA-6~10です。

また、回路構成が異なるDC-DCコンバータの問題も令和5年1月2回目A-9で出題されています。

【過去問解説】令和5年1月の1陸技試験問題を解いてみた（R5.1 2回目無線工学A A-6~A-10）

１陸技令和5年1月の無線工学A(2回目)の問題を解いてみました。今回はA-6~10です。

A

FETがONの時はDはに電流は逆方向になるのでDは非導通(OFF)となります。

そのため、Aには「非導通(OFF)」が入ります。

B

逆にFETがOFFの時はDは導通(ON)になります。

そのため、Bには「導通(ON)」が入ります。

C,D

Lの両端の電圧を考えます。コイルに流れる電流を$i_L$とすると \[ V_L=-L\frac{di_L}{dt} \\ di_L=-\frac{V_L}{L}dt \] となります。

FETがONの時はLの両端に$V_i$の電圧がかかるので \[ di_{LON}=-\frac{V_i}{L}T_{ON} \] となります。

一方FETがOFFの時は \[ di_{LOFF}=\frac{V_o}{L}T_{OFF} \] となります。 $V_o$の符号はFETがOFFの時は$V_o$はLに蓄えられたエネルギーで賄われるのでLと同じ方向になります。

回路が電流連続モードで理想的に動作するので \[ di_{LON}=di_{LOFF} \] となります。

そのため、 \[ V_o=-\frac{T_{ON}}{T_{OFF}}V_i \\ =-\frac{\frac{T_{ON}}{T_{ON}+T_{OFF}}}{1-\frac{T_{ON}}{T_{ON}+T_{OFF}}}V_i \\ =-\frac{D}{1-D}V_i \] で、Cには「$\frac{D}{1-D}$」が入ります。

また、$V_o$の符号は$V_i$の逆になっているので極性は②の方向でDには「②」が入ります。

以上から答えは4です。