令和6年7月の一陸技の試験の無線工学AのA-1~5の問題について解説します。
R.6.7 無線工学A A-1

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学A A-1
この問題は同様の問題が令和4年7月1回目A-1で出題されています。 文章も空欄の位置も全く同じです。
下記の記事をご参照ください。

他は過去問と一緒で
- A:逆離散フーリエ変換
- B:$a_n\cos (2\pi nf_st)-b_n\sin (2\pi nf_st)$
- C:$\cos (2\pi nf_ct)$
となり、答えは5です。
R.6.7 無線工学A A-2
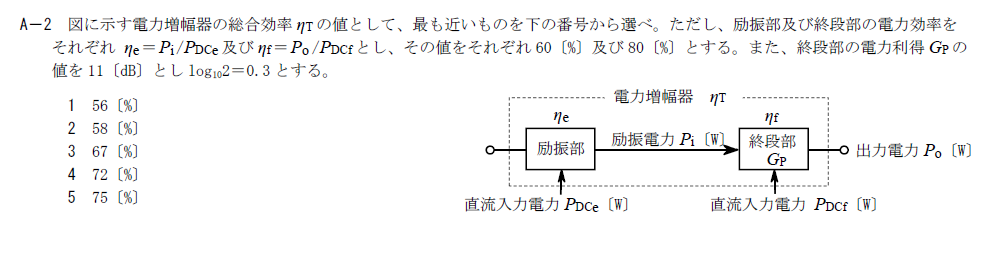
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学A A-2
電力増幅器の電力効率を求める問題です。
この問題については同様の問題が令和4年7月1回目A-4で出題されています。

\[ \eta_T=\frac{12.5P_i}{P_{i}/\eta_e+12.5P_i/\eta_f}=\frac{12.5}{1/0.6+12.5/0.8}=0.722 \]
以上から答えは4です。
R.6.7 無線工学A A-3
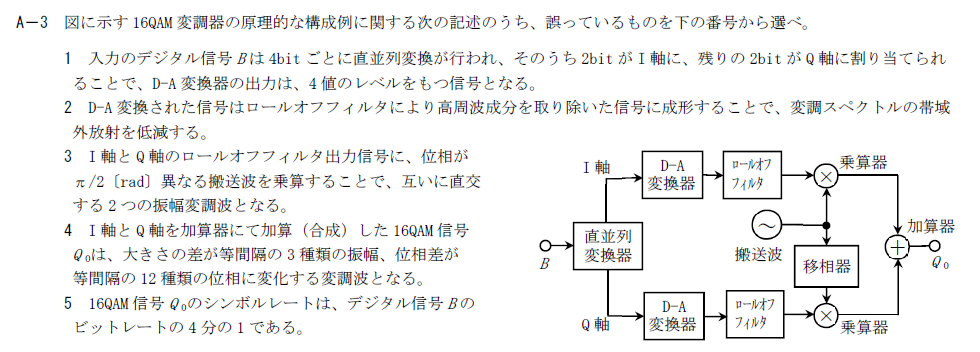
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学A A-3
16QAM変調器の原理的な構成について誤っている選択肢を選ぶ問題です
この問題は同様の問題が令和4年7月1回目A-3で出題されています。
下記の記事もご参照ください。

誤った選択肢は4です。
振幅が3種類、位相が12種類で正しいのですが等間隔ではありません。
そのため答えは4です。
R.6.7 無線工学A A-4
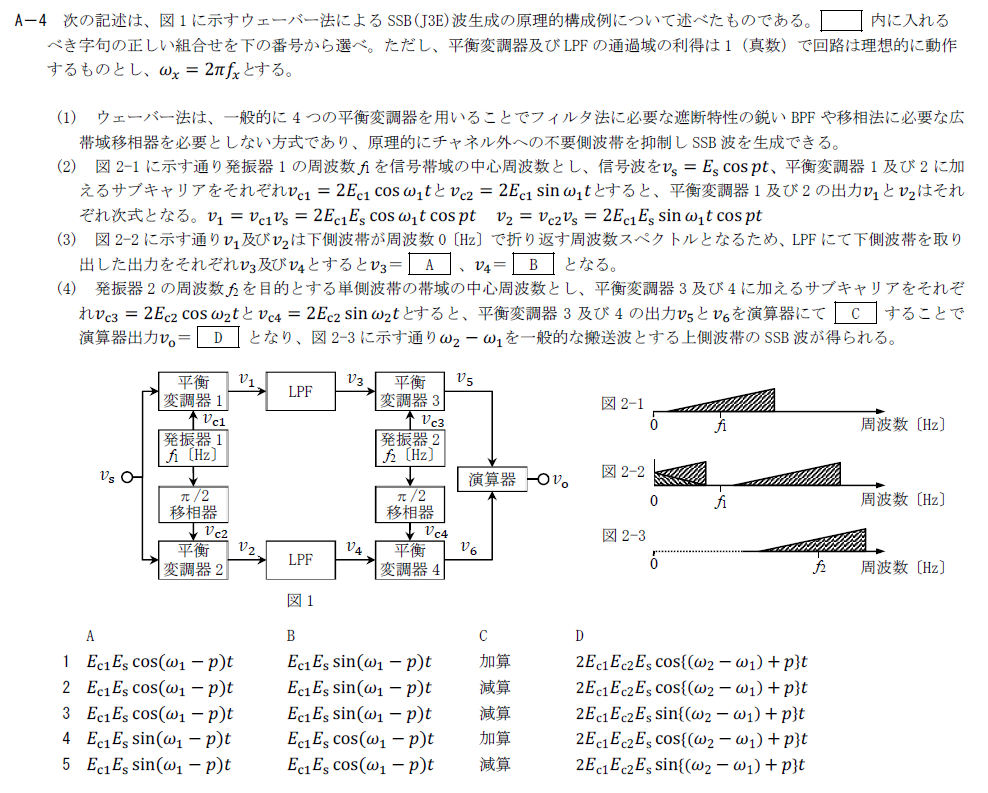
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学A A-4
ウェーバー法によるSSB波生成の原理に関する問題です。
ウェーバー法に関する問題はここ最近では出題されていないので新傾向と思ってよいでしょう。 内容自体を覚えていなくても問題の誘導に従って解いていきましょう。
A,B
(3)までは1段目の平衡変調器とそこから必要な信号を取り出すLPF出力に関する内容です。
平衡変調器の出力は(2)に記載されているのでこの式を変形して、低周波出力を計算しましょう。
\[ v_1=2E_{c1}E_S\cos \omega_1t\cos pt \\ =2E_{c1}E_S\frac{1}{2}\left\{\cos (\omega_1+p)t+\cos (\omega_1-p)t\right\} \\ =E_{c1}E_S\left\{\cos (\omega_1+p)t+\cos (\omega_1-p)t\right\} \] 同様に \[ v_2=2E_{c1}E_S\sin \omega_1t\cos pt \\ =E_{c1}E_S\left\{\sin (\omega_1+p)t+\sin (\omega_1-p)t\right\} \] LPFで出力されるのは低周波の$\omega_1-p$の成分です。 \[ v_3=E_{c1}E_S\cos (\omega_1-p)t \\ v_4=E_{c1}E_S\sin (\omega_1-p)t \]
そのため、A,Bそれぞれには
- A:$E_{c1}E_S\cos (\omega_1-p)t$
- B:$E_{c1}E_S\sin (\omega_1-p)t$
が入ります。
C,D
同様に$v_3$と$v_{c3}$および$v_4$と$v_{c4}$をそれぞれ掛け算した結果が$v_5,v_6$となるので \[ v_5=E_{c1}E_{c2}E_S\left\{\cos (\omega_2+\omega_1-p)t+\cos (\omega_2-\omega_1+p)t\right\} \\ v_6=E_{c1}E_{c2}E_S\left\{-\cos (\omega_2+\omega_1-p)t+\cos (\omega_2-\omega_1+p)t\right\} \] となります。
問題文から所望の信号の搬送波は$\omega_2-\omega_1$なので$v_5$と$v_6$を加算することで \[ v_O=2E_{c1}E_{c2}E_S\cos (\omega_2-\omega_1+p)t \] を取り出すことができます。
以上から
- C:加算
- D:$2E_{c1}E_{c2}E_S\cos (\omega_2-\omega_1+p)t$
が入り、答えは1です。
R.6.7 無線工学A A-5

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学A A-5
OFDMのマルチパスにより影響に関する問題です。
この問題についてもここ数年出題されていないようです。
A
合成波を計算していきます。 ここでは三角関数の合成を使います。一陸技ではあまり使わない気がします。
\[ S_O(t)=\cos 2\pi ft +r\cos \left\{2\pi f(t-t_d)+\theta\right\} \\ =\cos 2\pi ft +r\left\{\cos 2\pi ft \cos (2\pi ft_d-\theta)+\sin 2\pi ft \sin (2\pi ft_d-\theta)\right\} \\ =\left\{1+r\cos (2\pi ft_d-\theta)\right\}\cos 2\pi ft +r\sin (2\pi ft_d-\theta) \sin 2\pi ft \] 一旦ここで止めておいて、$\cos 2\pi ft$と$\sin 2\pi ft$の係数を考えます。 \[ \left\{1+r\cos (2\pi ft_d-\theta)\right\}^2+r^2\sin^2 (2\pi ft_d-\theta) \\ =1+2r\cos (2\pi ft_d-\theta) +r^2\cos^2(2\pi ft_d-\theta) +r\sin^2(2\pi ft_d-\theta) \\ =1+2r\cos (2\pi ft_d-\theta) +r^2 \] となり、これを$R^2$と置きます。
ここで三角関数を合成します。 \[ S_O(t)=R\left\{\frac{1+r\cos (2\pi ft_d-\theta)}{R}\cos 2\pi ft +\frac{r\sin (2\pi ft_d-\theta)}{R}\sin 2\pi ft\right\} \\ =R(\cos \phi \cos 2\pi ft +\sin \phi \sin 2\pi ft) \\ =R\cos (2\pi ft -\phi) \] この$\phi$は \[ \tan \phi =\frac{r\sin (2\pi ft_d-\theta)}{1+r\cos (2\pi ft_d-\theta)} \] となるので問題文の定義通りです。
ここでAには$R$が入ることになるので \[ R=\sqrt{1+2\cos (2\pi ft_d-\theta)+r^2} \] が入ります。
B
最大値になるのは希望波と遅延波が強めあうときで、最小値になるのは希望波と遅延波が弱めあうときなので振幅の比は \[ \frac{1+|r|}{1-|r|} \] となります。
そのため、Bには$(1+|r|)/(1-|r|)$が入ります。
C
図に記載されている通り、遅延時間の逆数の周波数の振幅リプルが起きます。
そのため \[ f_r=1/t_d \] となり、Cには$1/t_d$が入ります。
以上から答えは4です。
まとめ
今回は令和6年7月の無線工学Aの試験A-1~A-5の問題について解説しました。 今回はあまり見ない問題がいくつか出題されていました。 多くの場合は問題文に誘導がついているのでそこに従って落ち着いて問題に取り組みましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント