令和4年1月の1陸技の試験2回目の無線工学BのA-6~10の問題について解説します。
R.4.1 無線工学B(2回目) A-6
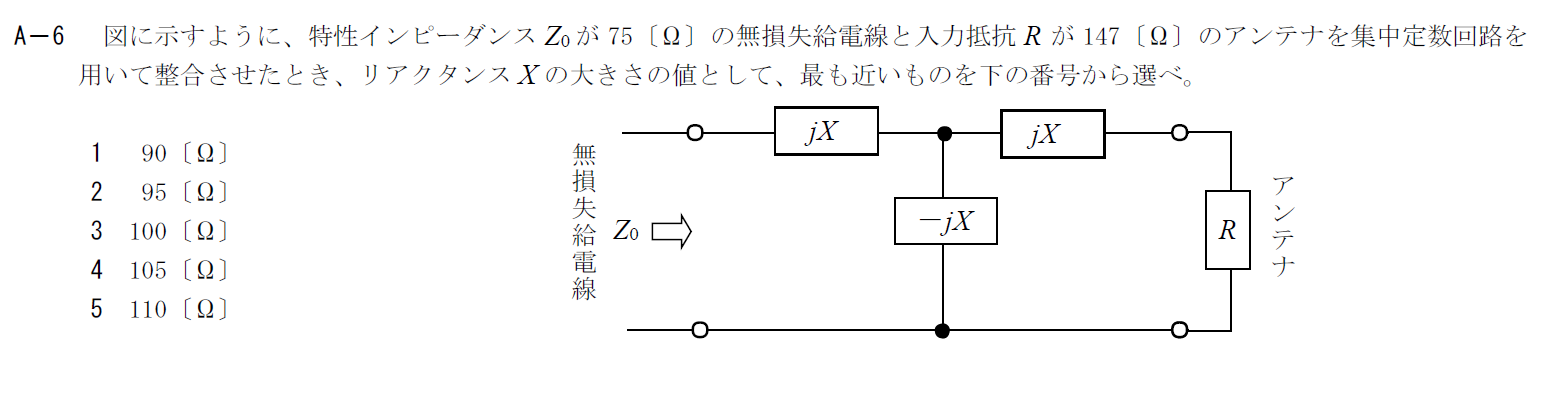
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B A-6
集中定数の整合回路に関する問題です。
給電線からみた整合回路とアンテナの合成インピーダンスを計算し、それが給電線と整合している(等しい)という条件で計算を進めましょう。
合成インピーダンス$Z$は次のように計算します。
\[
Z=jX+\left(-\frac{1}{jX}+\frac{1}{R+jX}\right) \\
=jX-\frac{jX(R+jX)}{R} \\
=\frac{X^2}{R}
\]
$Z=Z_0$なので、この式を$Xについて解くと
\[
X=\sqrt{RZ_0}=\sqrt{75 \times 147}=105
\]
となります。
真面目に素因数分解して解いてもいいですが、与えられた選択肢のどれに近いかがわかれば問題ありません。
そのため、
\[
\sqrt{75 \times 147} \simeq \sqrt{75 \times 150}=\sqrt{2 \times 75^2}\simeq 1.41 \times 75=105.75
\]
と求めることもできます。
以上から
答えは4です。
R.4.1 無線工学B(2回目) A-7

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B A-7
1/4波長整合回路に関する問題です。
整合用の給電線の直径を求める問題で多少面倒くさいので気をつけましょう。
まず、給電線からみた整合回路とアンテナのインピーダンス$Z_Q$を計算します。
給電線の特性インピーダンスを$Z_0$とすると、$Z_Q$は次のように表せます。
これは覚えておいたほうがいいでしょう。
\[
Z_Q=Z_0\frac{R\cos \beta l+jZ\sin \beta l}{Z\cos \beta l+jR\sin \beta l}
\]
1/4波長整合回路なので$\beta l=\pi /2$です。
すると
\[
Z_Q=Z_0\frac{Z_0}{R}
\]
と簡単に表せます。
給電線の特性インピーダンス$Z_0$、整合用給電線の特性インピーダンス$Z_1$を計算すると次のようになります。
ここで給電線の線間距離を$D_0$、直径を$d_0$、整合用給電線の線間距離を$D_1$、直径を$d_1$とします。
\[
Z_0=276\log_{10}\frac{2D_0}{d_0} \\
Z_1=276\log_{10}\frac{2D_1}{d_1}
\]
$Z_0=Z_Q$なので、次の式が成り立ちます。
\[
276\log_{10}\frac{2D_0}{d_0}=\frac{1}{R}\left\{ 276\log_{10}\frac{2D_1}{d_1}\right\}^2
\]
$D_0=50 \times 10^{-3}$、$d_0=1 \times 10^{-3}$$D_1=50 \times 10^{-3}$、$R=138$を代入して整理すると
\[
\log_{10}\frac{2D_0}{d_0}=2\left\{ 276\log_{10}\frac{2D_1}{d_1}\right\}^2 \\
(1+\log_{10}d)^2=1 \\
\log_{10}d=0,-2
\]
計算すると$d=1,0.01\rm{[m]}$となります。
選択肢にあるのは$0.01\rm{[m]}=10[\rm{mm}]$です。
計算上は直径1[m]の給電線でも使用できますが、現実的ではありません。
そのため、
答えは1です。
R.4.1 無線工学B(2回目) A-8

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B A-8
電磁波の導体への浸透に関する問題です。
A
(1)は表皮厚さの定義に関する記述です。
表皮厚さは導体中で電界強度が$1/e$になる導体表面からの距離です。
表皮厚さ$d$は$d=\sqrt{\frac{2}{\omega \mu \sigma}}$と表されます。 ここで$\omega=2\pi f$、$\mu$は透磁率、$\sigma$は導電率です。
そのため
、Aには「$1/e$」が入ります。
B
減衰定数が小さいほど、減衰せずに導体の内部に浸透できるので表皮厚さは厚くなります。
そのため、
Bには「厚く」が入ります。
C
Aで紹介した式の通り、表皮厚さは導電率のルートに反比例するので導電率が大きくなるほど表皮厚さは薄くなります。
感覚的には完全導体には電磁波は浸透できないので、導電率が大きいほど完全導体に近いので導電率が大きいほど表皮厚さは薄くなります。
そのため、
Cには「大きく」が入ります。
以上から
答えは1です。
R.4.1 無線工学B(2回目) A-9

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B A-9
同軸線路や導波管の伝送モードに関する問題です。
A
同軸線路は芯線と外部導体がコンデンサのような構造になっています。
そのため、断面で見ると芯線から放射状に電界ができ、磁界は芯線と同心円状にできます。
上記の通り、管軸方向には電磁界の成分は含まれないので、伝送モードはTEMモードです。
Aには「TEM」が入ります。
B
円形導波管の$TE_{01}$モードでは周波数が高くなるほど減衰定数が低下します。
この時、電界は管軸を中心とした同心円状に分布しているので、管壁を流れる電流が管軸に対して横方向にしか流れないためです。
そのため、
Bには「高く」が入ります。
C
方形導波管を$TE_{10}$モードで使用する時の周波数は$a<\lambda < 2a $の範囲ないを使用します。
波長が$2a$を超えると$TE_{10}$モードの電界分布を満たすことができなくなります。
そのため、
Cには「$2a$」が入ります。
以上から、答えは5です。
R.4.1 無線工学B(2回目) A-10

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B A-10
誘電体レンズアンテナに関して誤った選択肢を選ぶ問題です。
比誘電率$\epsilon_r$の誘電体レンズでは誘電体内の電波の速度が$1/\sqrt{\epsilon_r}$となります。
これにより、中心付近と外側で異なる速度でレンズを通過し、レンズ通過時に波面が揃った平面波となります。
誘電体の屈折率$n$は$n=\sqrt{\epsilon_r}$と表せるので、誤った選択肢は2です。
そのため、
答えは2です。
まとめ
今回は先日行われた令和4年1月2回目の1陸技の無線工学BのA-6~10を解いてみました。
計算が地味に面倒くさい問題も出題されますが、工夫したり、少しメタ的なテクニックを使って時間節約ができることも多いです。
出てくる数値が細かい時はなにか使える手段がないか考える癖をつけておきましょう。
勉強法
第一級陸上無線技術士の勉強法とおすすめ参考書
参考文献
電磁気学をちゃんと学びたい人向け
リンク
上の難易度が高い人
リンク
リンク








コメント