令和4年1月の1陸技2回目の試験、無線工学AのA-1～5の問題について解説します。
R.4.1 無線工学A（2回目） A-1
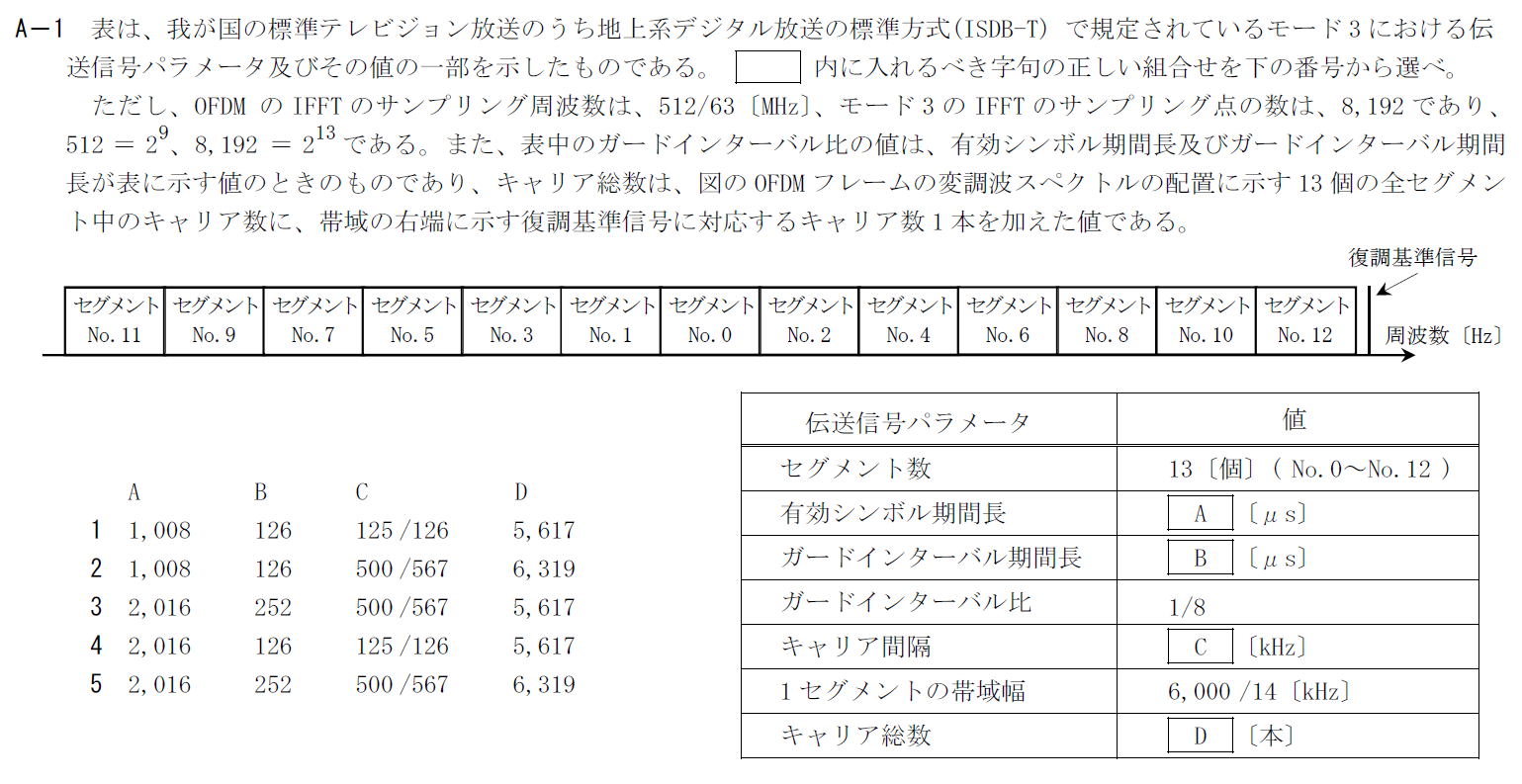
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-1
地上デジタル放送のモード3に於ける伝送信号のパラメータに関する穴埋め問題です。
モードは1~3の3つなので覚えておくこともできますが、今回は選択肢から推測して答えを導いてみましょう。
A,C
まず、AとCをセットで考えるのがいいでしょう。
BはAの結果から導けます。
有効シンボル期間長とキャリア間隔は逆数の関係になければなりません。
とりあえず、Aの選択肢にある1008$\rm{[\mu s]}$と2016$\rm{[\mu s]}$の逆数を計算してみましょう。
\[
\frac{1}{1008 \times 10^{-6}}=125/126 \\
\frac{1}{2016 \times 10^{-6}}=125/252
\]
となります。
Cとして適切なものは125/126しかないので、Aには1008、Cには125/126が入ります。
この段階で答えは1に決まりますが、他の空欄も見ておきましょう。
B
ガードインターバル比は(ガードインターバル期間長)/(有効シンボル期間長)となるので1008/8=126$[\rm{\mu s}]$です。
D
1セグメント辺りのキャリア数は(セグメント帯域幅)/(キャリア間隔)=$\frac{6000}{14}/\frac{125}{126}=432$です。
全部で13セグメント分に復調基準信号を表す1本を加えればキャリア総数になります。
そのため、Dには5617が入ります。
以上から答えは1です。
R.4.1 無線工学A（2回目） A-2
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-2
2つの単一正弦波による振幅変調波の電力を計算する問題です。
振幅変調の電力$P_m$は搬送波電力$P_c$と変調度$m$を使って
\[
P_m=P_c(1+m^2/2)
\]
となります。
ここから
\[
m=\sqrt{\frac{3P_m}{P_c}-2}
\]
と変調度を計算することができます。
問題では2つの単一正弦波による振幅変調を考えています。
この時の電力$P_{m2}$は変調度$m_1, m_2$を用いて
\[
P_m=P_c(1+m_1^2/2+m_2^2/2)
\]
です。
まず、問題文から$m_1=0.6$が読み取れます。
もう一方の変調度は先程の$m$を求める式から$m_2=0.8$が計算できます。
そのため、
\[
P_{m2}=10\times \left( 1+\frac{0.36}{2}+\frac{0.64}{2}\right)=15.0[\rm{kW}]
\]
です。
以上から答えは3の15.0[kW]です。
R.4.1 無線工学A（2回目） A-3
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-3
OFDMの原理的な最大伝送速度を求める問題です。
まず、1シンボル辺りの有効なビット数を計算します。
変調方式が256QAMなので、1シンボル1サブキャリア辺り8[bit]です。
符号化率が3/4なので1シンボル期間長辺り$8\times 50 \times \frac{3}{4}$bitとなります。
ガードインターバルも含めて$5[\rm{}]$で上記のビット数が伝送されるので、
\[
8\times 50 \times \frac{3}{4}/(5\times 10^{-6})=60 \times 10^{6}
\]
となります。
そのため、答えは4の60[Mbps]です。
R.4.1 無線工学A（2回目） A-4
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-4
QPSKとπ/4シフトQPSKの位相変化に関する問題です。
この問題は問題文の誘導どおりに解けば簡単に答えが出ます。
A
QPSKについては信号配置が与えられているので、図1を見ながら考えましょう。
IとQの極性が同時に変化するということは図1上で原点を挟んで反対側に映ったことを意味します。
このとき、位相はIQ平面上で原点を中心とした回転角なので、位相は$\pi$変化します。
そのため、Aには$\pi$が入ります。
B
一方、π/4シフトQPSKでは現在の位置によらず、前後の信号の位相変化で送られたデータを表現します。
問題文でそれぞれのデータに対して変化する位相が定義されているので、順番に決めていけばBが決まります。
時系列を表にまとめてみましょう。
| データ | 位相変化 | 位置 |
|---|---|---|
| 初期値 | – | ① |
| “0,1” | $+3\pi/4$ | ④ |
| “1,1” | $-3\pi/4$ | ① |
| “0,0” | $+\pi/4$ | ② |
| “1,0” | $-\pi/4$ | ① |
そのため、①④①②がBの答えです。
以上から答えは3です。
R.4.1 無線工学A（2回目） A-5
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-5
16QAMの理論的なビット誤りに関する問題です。
問題の文章量が多く見慣れないかもしれませんが、問題文の誘導に従って計算を進めればそれほど難しい問題ではありません。
QPSKでは同相、直交成分でそれぞれ同じ電力になるので、それぞれの信号電力は$A^2/2$となります。
(1)の2段落目の文章から$P_2=\frac{3}{2}P_1$、$P_3=2P_1$です。
1段落目で$P_{16QAM}$が与えられているので
\[
P_{16QAM}=(1/4)P_1+(1/2)P_2+(1/4)P_3 \\
=(1/4)P_1+(1/2)(3/2)P_1+(1/4)2P_1=\frac{3}{2}P_1
\]
となります。
(2)の文章から、C/Nが1/5倍、$P_{1}=\frac{1}{2}P_{QPSK}=1/4\rm{erfc}\{\sqrt{(C/N)/2}\}$となります。
これらの値を(1)から求めた式に代入すると
\[
P_{16QAM}=\frac{3}{2}\frac{1}{4}\rm{erfc}\{\sqrt{(C/5N)/2}\}=\frac{3}{8}\rm{erfc}\{\sqrt{(C/N)/10}\}
\]
です。
以上から答えは1です。
まとめ
今回は令和4年1月2回目の1陸技の無線工学AのA-1~5を解いてみました。
今回は問題の誘導に従って解ける問題が多かった印象です。問題文を落ち着いて読めば対策が不十分な問題でも十分解ける問題も多いです。
本番でも落ち着いて取り組みましょう。
次の7月の試験申込み期間に入りましたね。
そろそろ試験勉強も本格的になってきた頃でしょう。
本サイトも活用して合格を勝ち取ってください。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人
コメント