【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 2回目 無線工学B A-11~A-15）

令和4年1月の1陸技の試験2回目の無線工学BのA-11～15の問題について解説します。

R.4.1 無線工学B（2回目） A-11

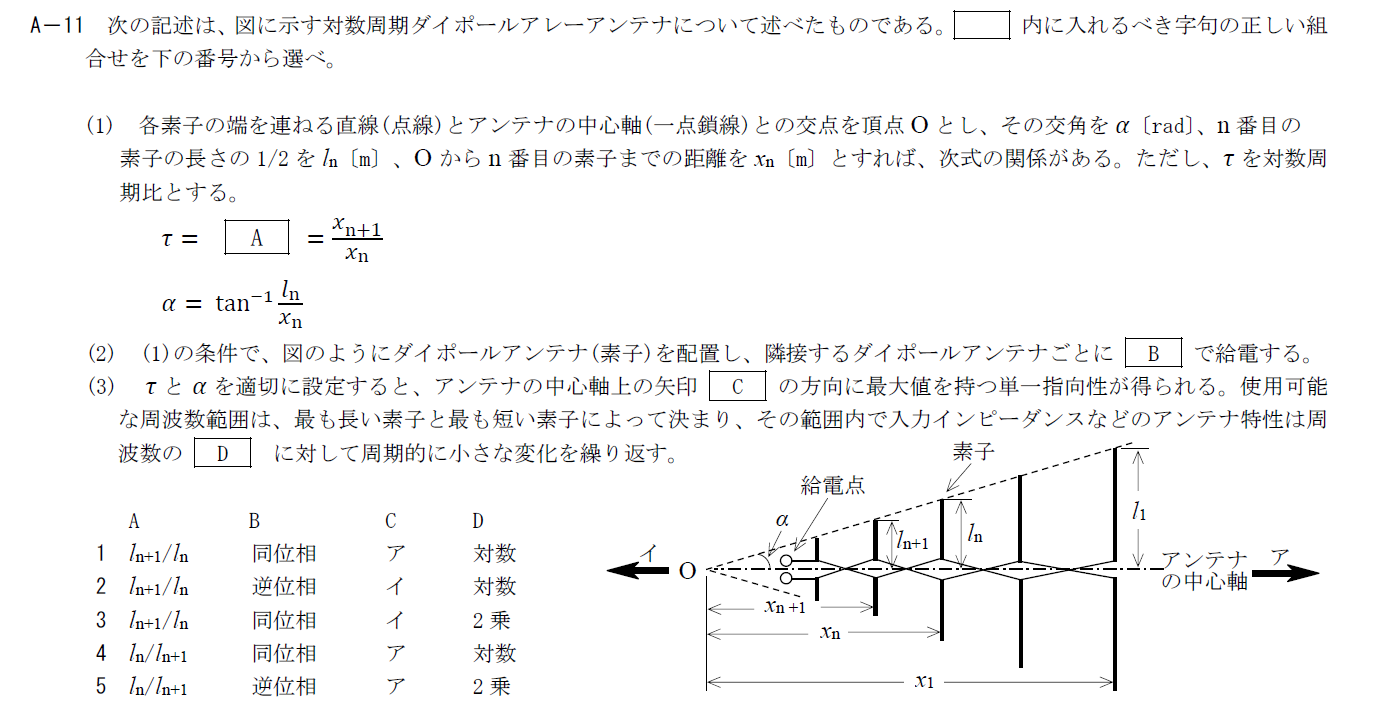
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月2回目　無線工学B A-11

対数周期ダイポールアレイアンテナ（ログペリ）に関する問題です。
対数周期アンテナについては色々深掘りしたいので別途別記事にまとめたいと思います。
気長にお待ち下さい。

A

対数周期アンテナの対数周期比は
$$\tau=\frac{l_{n+1}}{l_n}=\frac{x_{n+1}}{x_n}$$
となります。

そのため、Aには「$\frac{l_{n+1}}{l_n}$」が入ります。

B

対数周期ダイポールアレイでは隣接するダイポールアンテナごとに逆位相で給電します。

そのため、Bには「逆位相」が入ります。

C

対数周期ダイポールアレイアンテナは給電点方向、図でいうとイの方向に指向性を持ちます。

そのため、Cには「イ」が入ります。

D

対数周期ダイポールアレイアンテナは名前の通り周波数の対数に対して周期的な変化をします。

そのため、Dには「対数」が入ります。

以上から答えは2です。

R.4.1 無線工学B（2回目） A-12

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月2回目　無線工学B A-12

八木・宇田アンテナ（通称：八木アンテナ）について誤った選択肢を選ぶ問題です。

八木アンテナの放射器、反射器、導波器全てについて導体が太いほど帯域は広くなります。

そのため、誤った選択肢は3です。

それ以外はいずれも記載のとおりです。

以上から答えは3です。

R.4.1 無線工学B（2回目） A-13

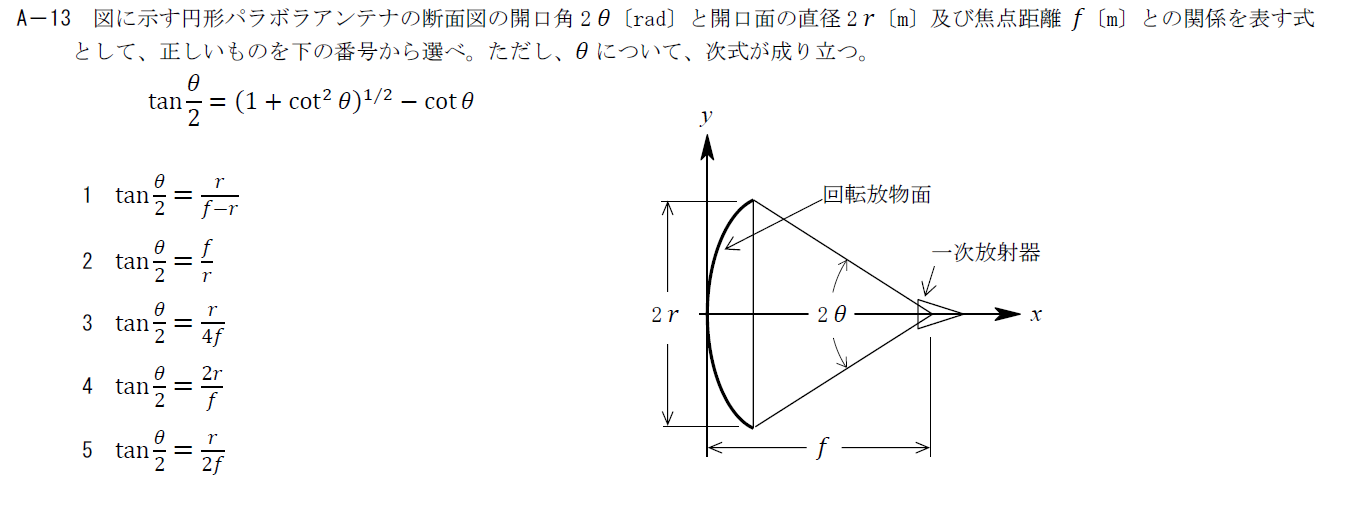
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月2回目　無線工学B A-13

この問題は令和3年1月の1回目A-13と全く同じです。

答えは5です。

下記をご参照ください。

【無線】1月の1陸技試験問題を解いてみた（R3.1 1回目　無線工学B A-11~A-15）

１陸技令和3年の無線工学Bの問題を解いてみました。今回は第2回A-11~15を解きました。

jr2kcb.com

2021.03.14

R.4.1 無線工学B（2回目） A-14

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月2回目　無線工学B A-14

移動体通信での電波の伝搬特性、特にフェージングに関する問題です。

A

(1)は建物などによるフェージングである、瞬時変動（マルチパスフェージング）に関する記述です。
問題文の通り、瞬時変動は建物などによる反射や回折で定在波が発生します。
建物などは移動しないため、定在波の分布は一意に決まります。
この中を移動局が移動することで、定在波の受信状況が変わるのでフェージングが発生するという流れです。

変動が早いということは定在波の変動が激しいことを意味しています。
強めあったり、弱めあったりする条件は波長によって決まり、波長が短い（＝周波数が高い）ほど定在波の空間による変動は激しくなります。
つまり周波数が高いほど早いフェージングが発生することになります。

そのため、Aには「高い」が入ります。

B

短区間中央値は実験的に対数正規分布に従うことが観測されています。

そのため、Bには「対数正規分布」が入ります。

C

(3)は周波数選択性フェージングについて記載されています。
周波数選択性フェージングは周波数による伝播による違いによって生じるフェージングです。

そのため、Cには「周波数選択性フェージング」が入ります。

D

周波数選択性フェージングは周波数による伝搬の相違により発生するので、帯域が広いほどその影響を受けやすくなります。
逆に、帯域を狭くすれば周波数選択性フェージングの影響は小さいです。

そのため、Dには「狭帯域」が入ります。

以上から、答えは3です。

R.4.1 無線工学B（2回目） A-15

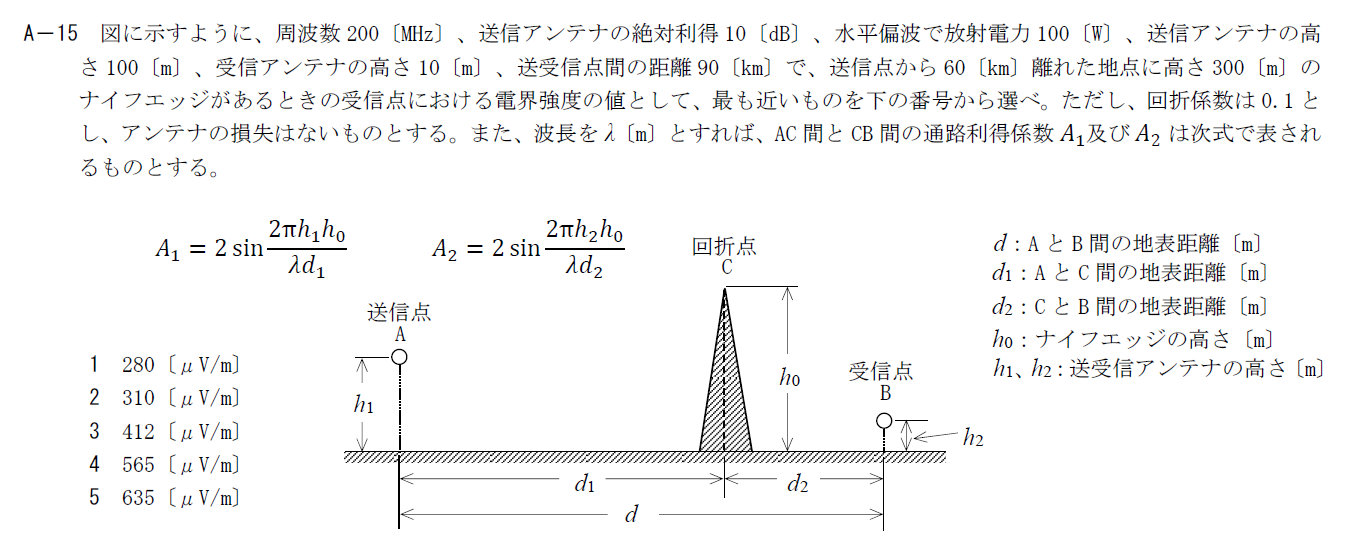
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月2回目　無線工学B A-15

回折を伴う電波の受信電界強度を求める計算問題です。

まず、電界強度の表式を考えましょう。
回折点を考えずに受信点Bがアンテナの最大放射方向にある時の受信点Bでの電界強度を$E_0$とします。
回折点を通る経路は最大放射方向とは異なるので通路利得係数$A_1,A_2$、回折係数$S$を考慮すると、受信点Bでの電界強度$E$とすると
$$E=E_0A_1A_2S$$
となります。

$E_0$は
$$E_0=\frac{\sqrt{30GP}}{d}=\frac{\sqrt{30\times 10 \times 100}}{90 \times 10^3}=\frac{\sqrt{3}}{9\times 10^2}$$
と表せます。

$A_1,A_2$を与えられた式から計算すると
$$A_1=2\sin \frac{2\pi \times 100 \times 300}{1.5 \times 60 \times 10^3}=\sqrt{3} \\ A_2=2\sin \frac{2\pi \times 10 \times 300}{1.5 \times 30 \times 10^3} \simeq \frac{8}{3}\pi \times 10^{-1}$$
となります。

以上から$E$を計算します。
$$E=\frac{\sqrt{3}}{9\times 10^2}\sqrt{3} \frac{8}{3}\pi \times 10^{-1} \times 0.1=\frac{8}{9}\pi \times 10^{-4}=279\times 10^{-6} [\rm{V/m}]\\ \simeq 280[\rm{\mu V/m}]$$

そのため、答えは１です。

まとめ

令和4年1月2回目の1陸技の無線工学BのA-11~15を解いてみました。
過去問と全く同じ問題（選択肢が少し違うだけ）も出題されています。
1陸技は過去問と同じまたは類似問題が出題されやすい試験なので、合格に向けた過去問演習は非常に重要となります。
このサイトのコンテンツも充実させていきたいと思いますので参考にしていただければ幸いです。

勉強法

第一級陸上無線技術士の勉強法とおすすめ参考書

参考文献

電磁気学をちゃんと学びたい人向け

上の難易度が高い人