令和5年1月の1陸技の試験2回目の無線工学AのA-16~20の問題について解説します。
R.5.1 無線工学A(2回目) A-16
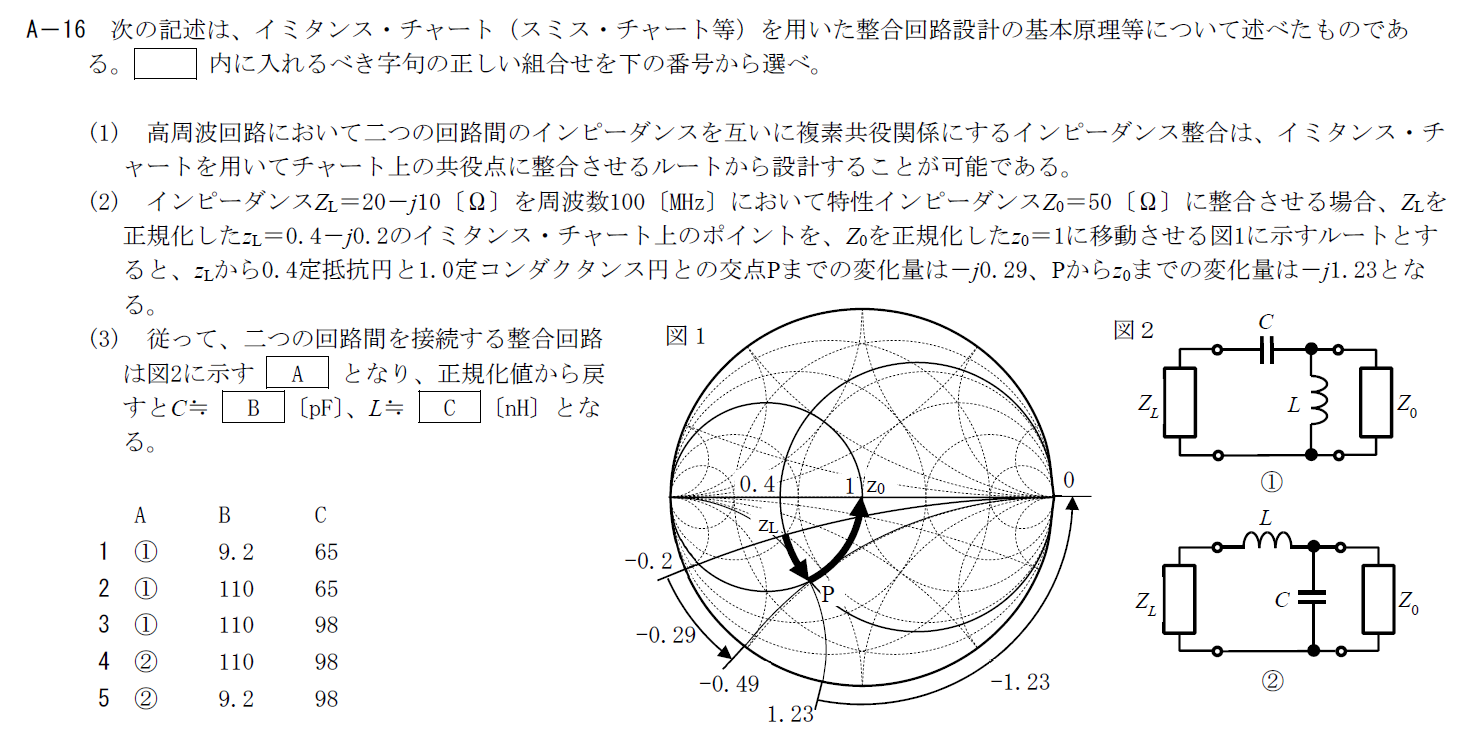
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-16
イミタンス・チャートに関する問題です。
イミタンス・チャートはスミス・チャートとアドミッタンス・チャートを重ね合わせたものです。
$Z=0$の点を通る線がスミス・チャートに由来するもの、$Z=\infty$の点を通る線がアドミッタンス・チャートに由来する線です。
スミス・チャート上の線は負荷に対して直列にインピーダンスを接続する時、アドミッタンス・チャート上の線は負荷に対してインピーダンスを並列に接続する時に使います。
A
$z_L\rightarrow P$では、スミス・チャートの定レジスタンス円を反時計回りに移動しています
これは負のインピーダンスをつないだことを意味します。 つまり、$Z_L$にコンデンサを直列につなげます。
次に$P\rightarrow z_0$では定コンダクタンス円を反時計回りに移動しています。
これは負のアドミッタンスを負荷に接続することを意味します。 つまり、$Z_L$にコイルを並列につなげます。
以上の条件にあうのは①の図なのでAには「①」が入ります。
B
$z_L\rightarrow P$の変化量が$-j0.29$なので、 \[ \frac{1}{j\omega C}=-j0.29Z_0 \\ C=\frac{1}{0.29Z_0\omega} \\ =\frac{1}{2\pi 100\times 10^6\times 0.29 \times 50} \\ =1.097\times 10^{-10}\rm{[F]} \\ \simeq 110\rm{[pF]} \] となります。
そのため、Bには「110」が入ります。
C
$P\rightarrow z_L$の変化量が$-j1.23$なので、 \[ \frac{1}{j\omega L}=\frac{-j1.23}{Z_0} \\ L=\frac{Z_0}{1.23 \omega} \\ =\frac{50}{2\pi 100\times 10^6 1.23} \\ =6.47 \times 10^{-8} \rm{[H]} \\ =65 \rm{[nH]} \] となります。
そのため、Cには「65」が入ります。
以上から、答えは2です。
R.5.1 無線工学A(2回目) A-17

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-17
MERの原理に関して誤った選択肢を選ぶ問題です。
誤った選択肢は5です。
CNRが低いほど誤差ベクトル成分が大きくなるので、CNRとMERの相関関係はなくなっていきます。 そのため、CNRとMERの線形性は低くなります。
つまり、CNRの推定精度は低くなるはずです
以上から答えは5です。
R.5.1 無線工学A(2回目) A-18
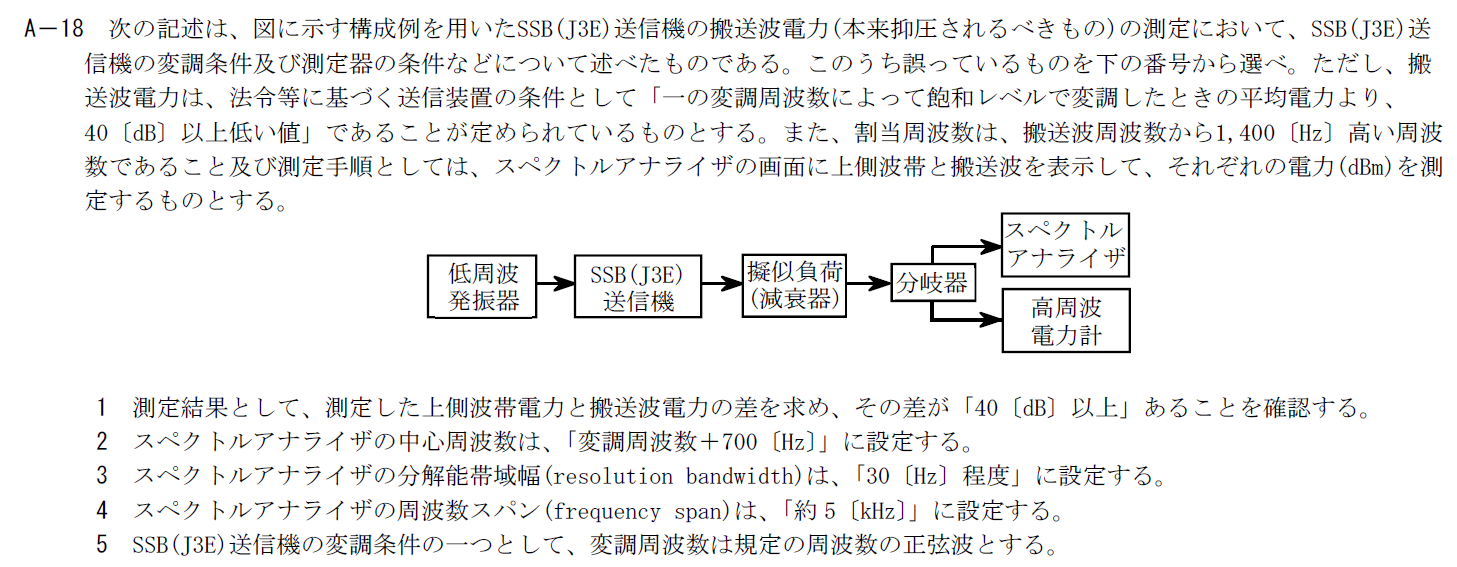
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-18
SSB送信機の測定に関して誤った選択肢を選ぶ問題です。
誤った選択肢は2です。
問題文に割り当て周波数が搬送波周波数から1400[Hz]高い周波数となっているので、上側側波帯の変調周波数は搬送波周波数+1400[Hz]となることを意味します。
上側側波帯と抑圧された搬送波周波数の両方を見る必要があるので中心周波数は搬送波周波数にするのが適切です。
変調周波数+700[Hz]だと上側側波帯からさらに搬送波周波数から離れた中心周波数となってしまいます。
そのため、答えは2です。
R.5.1 無線工学A(2回目) A-19

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-19
スペクトルアナライザとFFTアナライザについて測定できる項目の問題です。
A
信号に含まれる個々の正弦波の周波数についてはいずれの測定器でも測定できます。
そのため、Aには「できる」が入ります。
B
個々の正弦波の振幅についても同様に測定することができます。
そのため、Bには「できる」が入ります。
C
スーパヘテロダイン方式のスペクトルアナライザは局部発振器の周波数を掃引することで、周波数軸上で信号の周波数と振幅を測定します。
しかし、時間軸上の波形の測定はできません。
そのため、Cには「できない」
D
FFTアナライザは入力信号を離散フーリエ変換することで周波数軸上で信号の周波数、振幅そして位相を測定することができます。
各正弦波の位相が分かるのでそれぞれの相対位相も測定することができます。
そのため、Cには「できる」が入ります。
R.5.1 無線工学A(2回目) A-20

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-20
$\pi$型アッテネータの計算問題です。
T型アッテネータの同種の問題が令和4年1月1回目のA-19で出題されています。 こちらも合わせて押さえておきましょう。
下記の記事もご参照ください。

計算の方針は上記の記事と同じです。
信号源から流れる電流を$I$、負荷を流れる電流を$I_Z$、信号源からの出力電圧を$V_I$、負荷の両端の電圧を$V_O$とします。
入出力の整合は取れているので、電圧減衰率$K$は次のように表せます。 \[ K=\frac{V_2}{V_1}=\frac{Z_0I_Z}{Z_0I}=\frac{I_Z}{I} \]
減衰量が$-8\rm{[dB]}$なので、 \[ 20\log K=-8 \\ \log K=-0.4=\log 2^2 -\log 10 =\log \frac{4}{10}\\ K=\frac{2}{5} \]
各電圧と電流を図のように定義します。
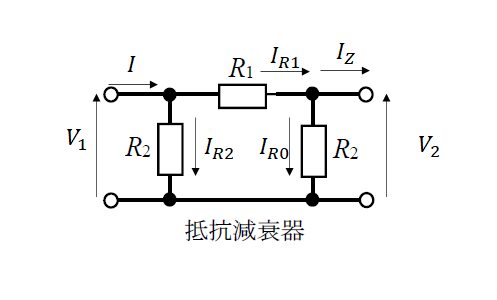
各変数の定義
電流について考えると \[ I=I_{R1}+I_{R2} \\ I_{R1}=I_{R0}+I_Z \] が成り立ちます。
2本目の式を1本目の式に代入すると \[ I=I_{R2}+I_Z+I_{R2} \] となります。
一方入力電圧と抵抗から \[ I_{R0}=\frac{V_2}{R_2}=\frac{I_Z Z_0}{R_2} \\ I_{R2}=\frac{V_1}{R_2}=\frac{I_Z Z_0}{R_2} \] なので、 \[ I=\frac{I_Z Z_0}{R_2}+I_Z+\frac{I_Z Z_0}{R_2} \] です。
この式を$R_2$について解くと \[ R_2=\frac{1+K}{1-K}Z_0 \]
一方、$R_1$にかかる電圧を考えると \[ R_1I_{R1}=V1-V_2 \] となるので、これを$I_{R1}=I_{R0}+I_Z$に代入すると \[ \frac{V_1-V_2}{R_1}=\frac{V_2}{R_2}+I_Z \] となります。
これを$R_1$について解くと \[ R_1=\frac{1-K^2}{2K}Z_0 \] となります。
求めたいのは$R_1$なので$R_1$の式に$K=2/5$を代入すると \[ R_1=21Z_0/20 \] です。
以上から答えは5です。
まとめ
今回は令和5年1月の無線工学A(2回目)の試験A-16~A-20の問題について解説しました。 後半は知識問題も多くなってきます。覚えてなくても論理的に考えれば答えが分かることも多いのであきらめずにしっかり問題文を読んでみましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント