令和5年1月の1陸技の試験2回目の無線工学AのA-11~15の問題について解説します。
R.5.1 無線工学A(2回目) A-11

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-11
航空用DMEの原理に関する問題です。
AとBは知識問題なので、この装置について覚えている必要があります。
DMEは地上のトランスポンダ(質問機)と航空機上のインタロゲータ(応答機)から構成される二次レーダです。
A
航空用DMEでは962~1213MHzのUHF帯の周波数が使用されます。
そのため、Aには「UHF」が入ります。
B
DMEでは質問信号と応答信号は異なる周波数が使用されます。 その周波数差は63MHzです。
そのため、Bには「異なる」が入ります。
C
問題文から \[ 420-50=370\rm{[\mu s]} \] で電波が往復することになります。
そのため、航空機とトランスポンダの距離は \[ 3\times 10^{8}\times 370 \times 10^{-6}/2=5.55 \times 10^4\rm{m} \] となります。
問題文から$1\rm{[nm]}=1852\rm{[m]}$なので \[ 5.55 \times 10^{4}/1852=30\rm{[nm]} \] となります。
ちなみに$\rm{[nm]}$は海里を表す単位でナノメートルではないので気をつけましょう。
以上から、答えは4です。
R.5.1 無線工学A(2回目) A-12
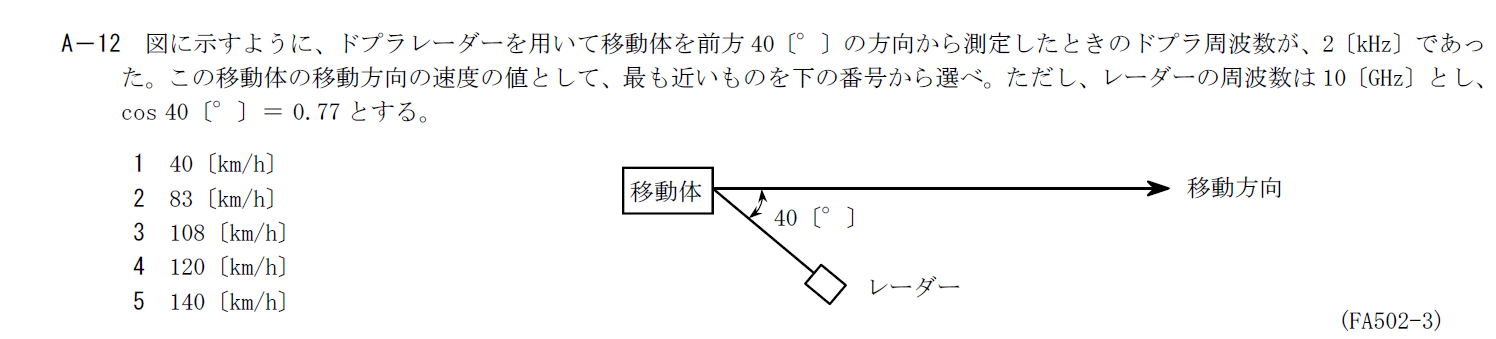
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-12
ドプラレーダに関する計算問題です。
レーダとの距離が$R$の物体の間を電波が往復したときの全位相角を$\phi$とすると \[ \phi =\frac{2R}{\lambda}2\pi =\frac{4\pi R}{\lambda} \] となります。
物体が移動しているとドプラによる変位角周波数$\omega_d$は \[ \omega_d=\frac{d\phi}{dt}=\frac{4\pi}{\lambda}\frac{dR}{dt}=\frac{4\pi v}{\lambda} \] です。 ここで$v$は物体のレーダとの相対速度です。
これを周波数に直すと \[ f_d=\frac{2v}{\lambda} \] 物体の移動方向によって符号が変わります。 近づくときはプラス、遠ざかるときはマイナスです。
この計算を問題文に当てはめます。 移動速度を$v_0$とすると、相対速度$v$は \[ v=v_0\cos \theta \] で。$\theta$は移動体から見たレーダの方向です。
$v$を代入して計算したい$v_0$について解くと \[ v_0=\frac{f_d \lambda}{2\cos \theta}=\frac{f_d c}{2f\cos \theta} \\ =\frac{2\times 10^3\times 3 \times 10^8}{2\times 10 \times 10^9\times 0.77} \\ =38.96\rm{[m/s]}=140.3\rm{[km/h]} \] となります。
以上から答えは5です。
R.5.1 無線工学A(2回目) A-13
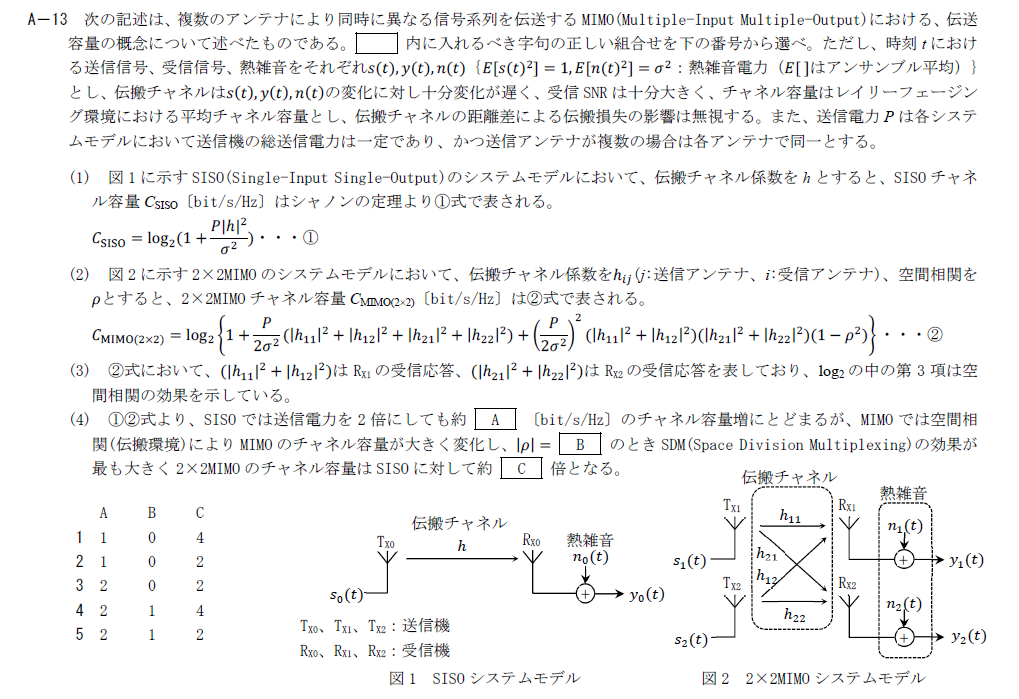
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-13
MIMOの伝送容量に関する問題です。
基本となる計算式が問題文に記載されているので順番に読んでいって解くのがよいでしょう。
A
AはSISOに関する空欄です。
①の式で$P \rightarrow 2P$に変更すると \[ C_{SISO}=\log_2\left( 1+\frac{2P|h|^2}{\sigma^2}\right) \\ =\log_22\left(\frac{1}{2}+\frac{P|h|^2}{\sigma^2}\right) \\ =\log_22+\log_2\left(\frac{1}{2}+\frac{P|h|^2}{\sigma^2}\right) \] となります。
対数関数は増加関数なので$\log_2\left(\frac{1}{2}+\frac{P|h|^2}{\sigma^2}\left) < \log_2\right(1+\frac{P|h|^2}{\sigma^2}\right)$なので、高々$\log_22=1$程度しか変化しないことになります。
そのため、Aには「1」が入ります。
B
②の式では$\{ \}$内の第3項のみ$\rho$に依存します。
$(1-\rho^2)$の係数はゼロ以上の値しかとらないので、$(1-\rho^2)$が最大値の$1$をとるときSDMの効果が最大になると言えます。
そのため、Bには「0」が入ります。
C
②の式を見やすくするために$|h_1|^2=|h_{11}|^2+|h_{12}|^2, |h_2|^2=|h_{21}|^2+|h_{22}|^2$と置きます。 \[ C_{MIMO}=\log_2\left\{1+\frac{P}{2\sigma^2}(|h_1|^2+|h_2|^2)\left( \frac{P}{2\sigma^2}\right)^2|h_1|^2|h_2|^2\right\} \\ =\log_2\left\{\left( 1+\frac{P|h_1|^2}{2\sigma^2}\right)\left( 1+\frac{P|h_2|^2}{2\sigma^2}\right)\right\} \] ここで、$|h_1|^2=|h_2|^2=2|h|$と仮定すると \[ C_{MIMO}=\log_2\left(1+\frac{P|h|^2}{2\sigma^2}\right)^2=2C_{SISO} \]
そのため、Cには「2」が入ります。
以上から答えは2です。
R.5.1 無線工学A(2回目) A-14

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-14
TDMAの方式に関する問題です。
この問題は令和3年7月1回目A-16で類題が出題されています。
こちらの記事も参考にしてください。

A
TDMA方式は時間によって使用する地球局を切り替えるので中継器を同時に使っている地球局は必ず1局以下です。 つまり使っている1局は飽和領域で中継器を使うことができます。
そのためAには「できる」が入ります。
B
地球局はバーストと呼ばれる信号をスロットの時間内に納めて創出します。
そのため、Bには「バースト」が入ります。
この空欄は令和3年7月1回目A-16のBと同じです。
C
各地球局が異なる時間に電波を送出するので混変調の問題がなくなります。
そのため、Cには「混変調」が入ります。
この空欄は令和3年7月1回目A-16のCと同じです。
以上から答えは2です。
R.5.1 無線工学A(2回目) A-15

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-15
誤り訂正符号に関する問題です。
この問題は令和3年7月1回目B-3で類題が出題されています。
下記の記事もご参照ください。

A
符号化率は符号語全体の中のチェックビットの割合です。
そのため、Aには「$k/n$」が入ります。
これは令和3年7月1回目B-3 ウの空欄と同じです。
B
ビタビ符号とリード・ソロモン符号のうちブロック符号に分類されるのはリード・ソロモン符号です。
そのため、Bには「リード・ソロモン」が入ります。
C
問題文の内容に一致する符号はターボ符号です。
そのため、Cには「ターボ符号」が入ります。
以上から答えは3です。
まとめ
今回は令和5年1月の無線工学A(2回目)の試験A-11~A-15の問題について解説しました。 知識だけでなく問題文の誘導に従って答えを導き出す問題も例年数問出題されます。 複雑な計算式に面食らうかもしれませんが、そのような問題の方が問題文を読めば解きやすいことも多いので、取りこぼさないようにしましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント