令和4年1月の1陸技の試験、無線工学AのA-16～20の問題について解説します。
R.4.1 無線工学A（1回目） A-16
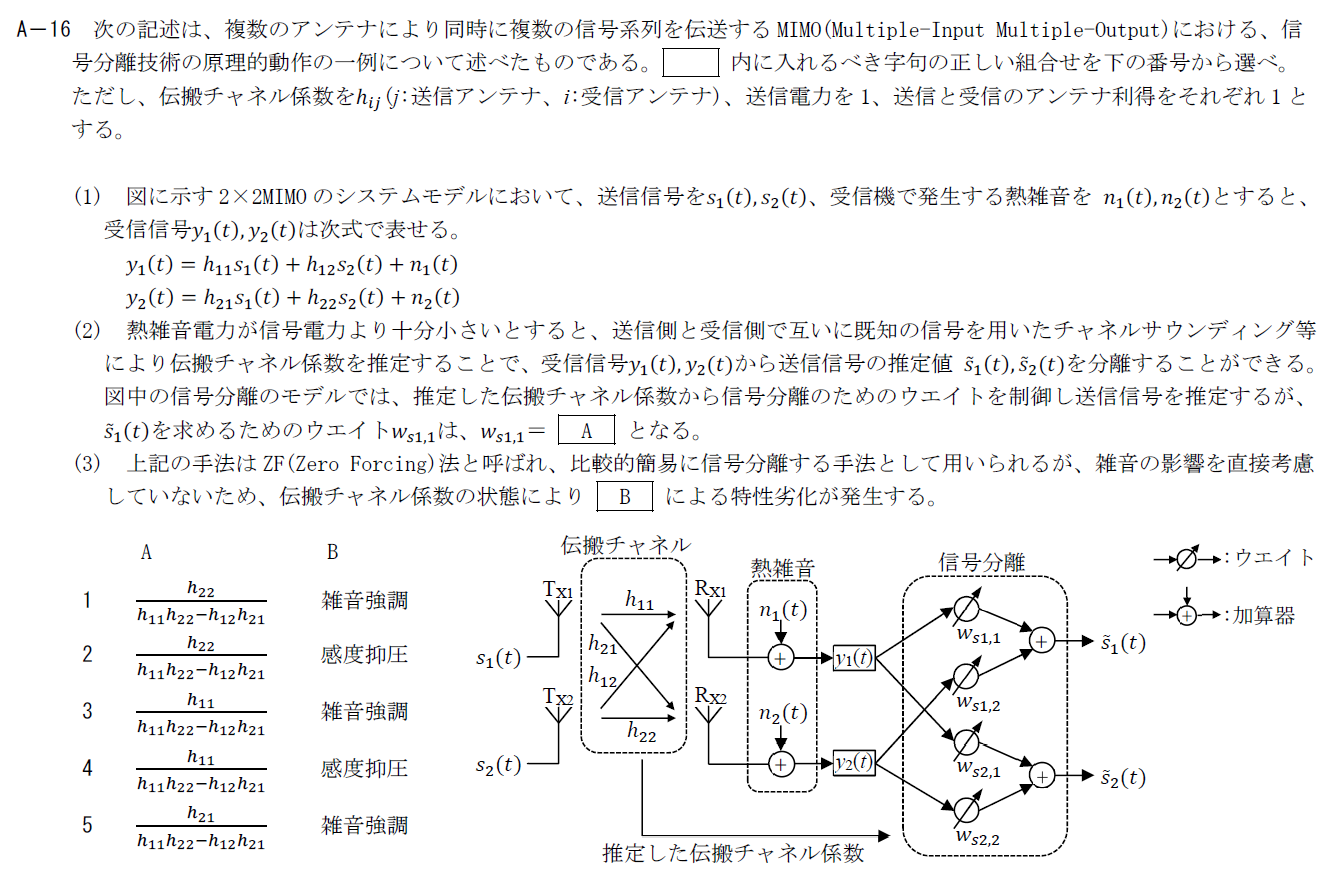
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学A A-16
MIMOシステムでの信号分離の原理に関する問題です。
ゴリ押しで連立方程式を解くこともできますが、行列を使うと比較的簡単に解くことができます。
A
まず、(1)で与えられた式を扱いやすい形に書き直しましょう。
ここでは連立方程式を行列を使って書き下します。
\[
\begin{pmatrix}
y_1(t) \\
y_2(t) \\
\end{pmatrix}
=
\begin{pmatrix}
h_{11} & h_{12} \\
h_{21} & h_{22} \\
\end{pmatrix}
\begin{pmatrix}
s_1(t) \\
s_2(t) \\
\end{pmatrix}
+
\begin{pmatrix}
n_1(t) \\
n_2(t) \\
\end{pmatrix}
\]
これを次のように表記することにします。
\[
\vec{y}=H\vec{s}+\vec{n}
\]
推定値$\vec{\tilde{s}}$が$\vec{s}$と一致するようにウエイトを決めます。
ウエイトの行列を$W$とすると
\[
\vec{\tilde{s}}=W\vec{y}=WH\vec{s}+W\vec{n}
\]
と表せます。
一旦、雑音を無視すると$W$が$H$の逆行列である必要があります。
$H$の逆行列を計算すると
\[
W=
\frac{1}{h_{11}h_{22}-h_{12}h_{21}}
\begin{pmatrix}
h_{22} & -h_{12} \\
-h_{21} & h_{11} \\
\end{pmatrix}
\]
となります。
そのため、Aには$w_{s1,1}=\frac{h_{22}}{h_{11}h_{22}-h_{12}h_{21}}$となります。
B
Aの結果からも分かる通り、雑音を計算に入れていないので、$W\vec{n}$が残ります。
$W$は$H$の逆行列なので、雑音が増幅されることがあります。
そのため、Bには「雑音強調」が入ります。
以上から答えは1です。
R.4.1 無線工学A（1回目） A-17
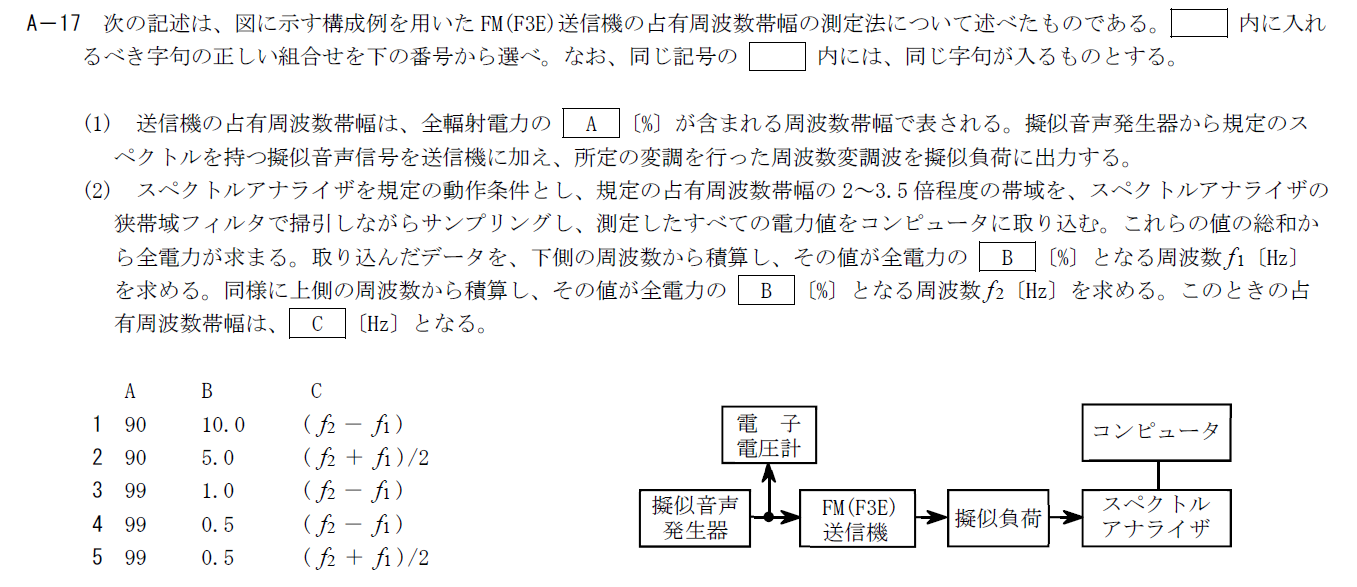
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学A A-17
FMの占有帯域幅の測定法に関する問題です。
A
電波法で全輻射電力の99%が含まれる周波数帯幅と定義されています。
そのため、Aには「99」が入ります。
B,C
占有周波数帯域に全電力の99%が含まれるので、下側から積算して全電力の0.5%となる周波数が占有周波数帯域の下限の周波数となります。上限も同様です。
占有帯域幅は上限から下限の周波数を引けばいいので$f_2-f_1$となります。
そのため、Bには「0.5」、Cには「$f_2-f_1$」が入ります。
以上から答えは4です。
R.4.1 無線工学A（1回目） A-18
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学A A-18
デジタルオシロスコープのサンプリング方式に関する問題です。
サンプリング方式には主に実時間サンプリング方式と等価時間サンプリング方式があります。
実時間サンプリング方式は高いサンプリング周波数で入力信号をサンプリングします。
サンプリング周波数の1/2倍（ナイキスト周波数）以上の周波数が入力されると元の信号を再現できずに折り返し誤差（エイリアシング）が発生します。
一方、等価時間サンプリング方式は数回に分けてサンプリングする手法です。
等価サンプリング方式にはシーケンシャルサンプリング方式とランダムサンプリング方式があります。
シーケンシャルサンプリングはサンプリング毎に一定時間ずつサンプリング時間を遅らせてサンプリングします。
ランダムサンプリング方式は入力信号をランダムにサンプリングして、全データを合わせて波形を再生します。
等価時間サンプリングでは繰り返しサンプリングを行う特性上、繰り返し波形の測定に適しています。
4の記述のみ上の説明に反していますので、誤った選択肢は4です。
実時間サンプリングと等価時間サンプリングが逆で、等価時間サンプリングではエイリアシングは発生せず、実時間サンプリングでエイリアシングが発生します。
そのため、答えは4です。
R.4.1 無線工学A（1回目） A-19
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学A A-19
T型アッテネータに関する計算問題です。
信号源から流れる電流を$I$、負荷を流れる電流を$I_Z$、信号源からの出力電圧を$V_1$、負荷の両端の電圧を$V_2$とします。
入出力の整合は取れているので、電圧減衰率$K$は次のように表せます。
\[
K=\frac{V_2}{V_1}=\frac{Z_0I_Z}{Z_0I}=\frac{I_Z}{I}
\]
減衰量が$14\rm{dB}$なので、
\[
20\log K=-14
\]
が成り立ちます。
$K$について解くと
\[
\log K=-0.7=0.3-1=\log 2 -1 =\log \frac{1}{5} \\
K=\frac{1}{5}
\]
$K$を使って$R_2$を計算できれば答えが出せます。
まず、$R_2$の両端の電圧を考えます。
$R_1$と$Z_0$の直列接続と並列に接続されているので、次の関係になります。
\[
R_2(I-I_Z)=(R_1+Z_0)I_Z \\
I_Z=\frac{R_2}{R_1+R_2+Z_0}I \\
K=\frac{R_2}{R_1+R_2+Z_0}
\]
信号源から見た回路のインピーダンスは$R_1+\frac{R_2(R_1+Z_0)}{R_1+R_2+Z_0}$となります。
整合が取れているのでこのインピーダンスは$Z_0$となります。
すると
\[
Z_0=R_1+\frac{R_2(R_1+Z_0)}{R_1+R_2+Z_0}=R_1+K(R_1+Z_0)
\]
となり、
\[
R_1=\frac{1-K}{1+K}Z_0
\]
が成り立ちます。
これを$K$の表式に代入して$R_2$について解くと
\[
R_2=\frac{2K}{1-K^2}Z_0
\]
となります。
$K=1/5$を代入すれば$R_2=\frac{5}{12}Z_0$となります。
以上から答えは5です。
R.4.1 無線工学A（1回目） A-20
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学A A-20
ベクトルネットワークアナライザ(VNA)に関する問題です。
内容的にはSパラメータに関する問題と考えていただいたほうが近いかもしれません。
A
Aは$a_2=0$の時の$S_{11}$がどうなるか聞かれています。
単純に$a_2=0$を代入すれば$b_1=S_{11}a_1$となるので、$S_{11}=b_1/a_1$となります。
そのため、Aには$b_1/a_1$が入ります。
B
$R_L$の表式から$R_L=-20\log |S_{11}|$なので、$b_1$が大きくなるほど$R_L$は小さくなります。
そのため、Bには「小さく」が入ります。
C
Aと同様に解けば$S_{21}=b_2/a_1$となります。
そのため、Cには$b_2/a_1$が入ります。
以上から答えは2です。
まとめ
今回は先月行われた令和4年1月1回目の1陸技の無線工学AのA-16~20を解いてみました。
無線工学Aでも計算問題は何問か出題されます。
面倒なものから簡単なものまでいろいろですが、取りこぼしの内容に対策しておきましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人
コメント