令和4年7月の1陸技の試験、無線工学AのA-16~20の問題について解説します。
R.4.7 無線工学A(2回目) A-16
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-16
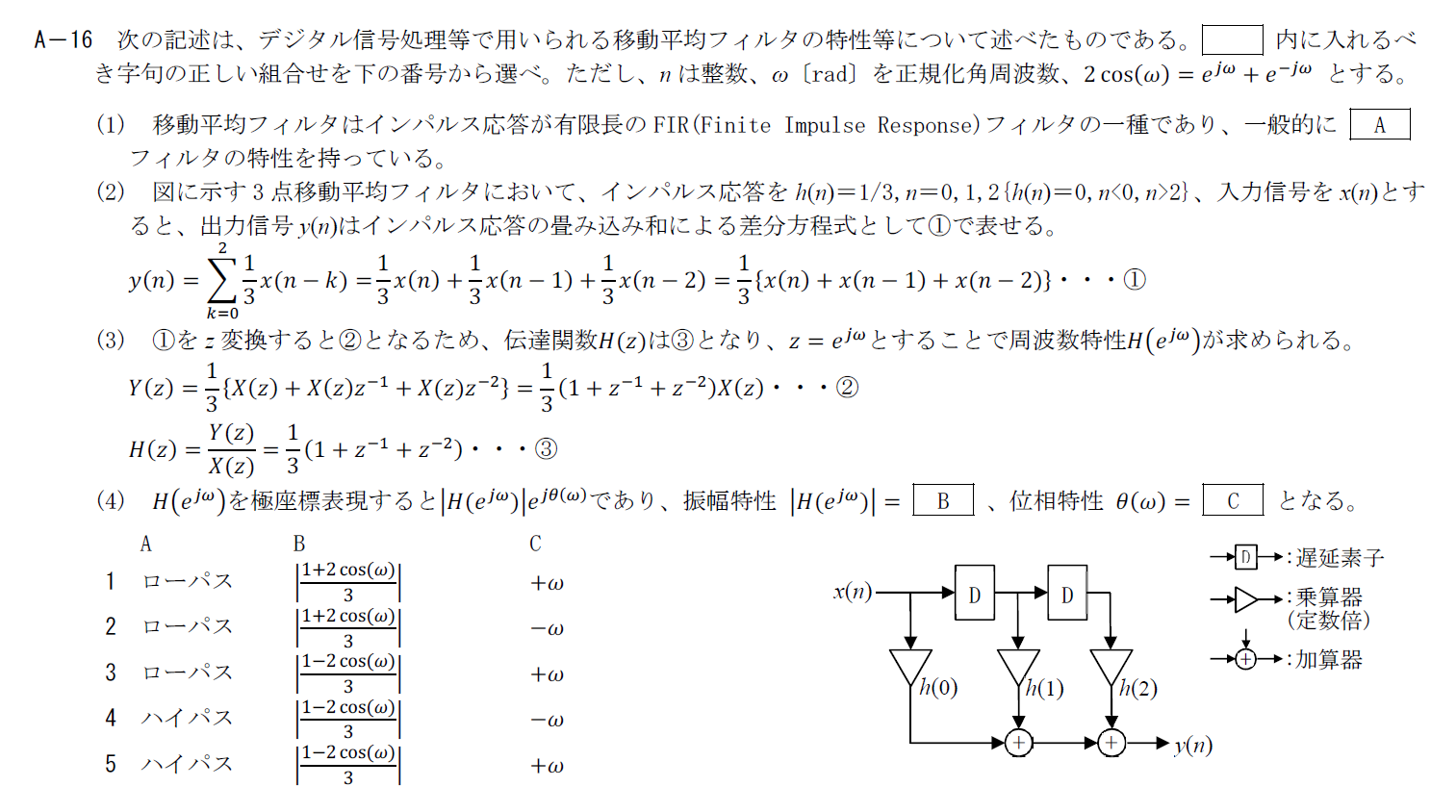
デジタル信号処理等で使用する移動平均フィルタに関する問題です。
A
(1)はFIRに関する記述です。 一般にFIRはローパスフィルタとして働きます。
そのため、Aには「ローパス」が入ります。
B,C
$z=e^{j\omega}$として、$H(e^{j\omega})$を計算してみます。 \[ H(e^{j\omega})=\frac{1}{3}(1+e^{-j\omega}+e^{-2j\omega}) \\ =\frac{1}{3}e^{-j\omega}(e^{j\omega}+e^{-j\omega}+1) \\ =\frac{1}{3}e^{-j\omega}(2\cos \omega +1) \]
$|e^{-j\omega}|=1$なので、上記の計算結果から \[ |H(e^{j\omega})|=\left|\frac{1+2\cos \omega}{3}\right| \] 位相を表すのは$e$のべきの中なので$e^{-j\omega}$が位相を表します。
そのため、Bには「$\left|\frac{1+2\cos \omega}{3}\right|$」、Cには「$-\omega$」が入ります。
以上から答えは2です。
R.4.7 無線工学A(2回目) A-17

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-17
スペクトルアナライザを用いたAM送信機の変調度測定に関する問題です。
A
(2)の文中で$m_a A/2$を$S$とするとあるので、 \[ m_aA/2=S \] となります。
この式を変形して \[ m_a=2S/A \] です。
そのため、Aには「$2S/A$」が入ります。
B
振幅の差が12[dB]となるので、$20\log A/S=12$です。
計算すると \[ \log A-\log S=0.6 \\ \log S=\log A -2\log 2=\log A/4 \\ S=A/4 \] となります。
Aの式に代入すると次のようになります。 \[ m_a=2S/A=\frac{1}{2} \] この結果から変調度は50%です。
そのため、Bには「50」が入ります。
以上から答えは3です。
R.4.7 無線工学A(2回目) A-18
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-18
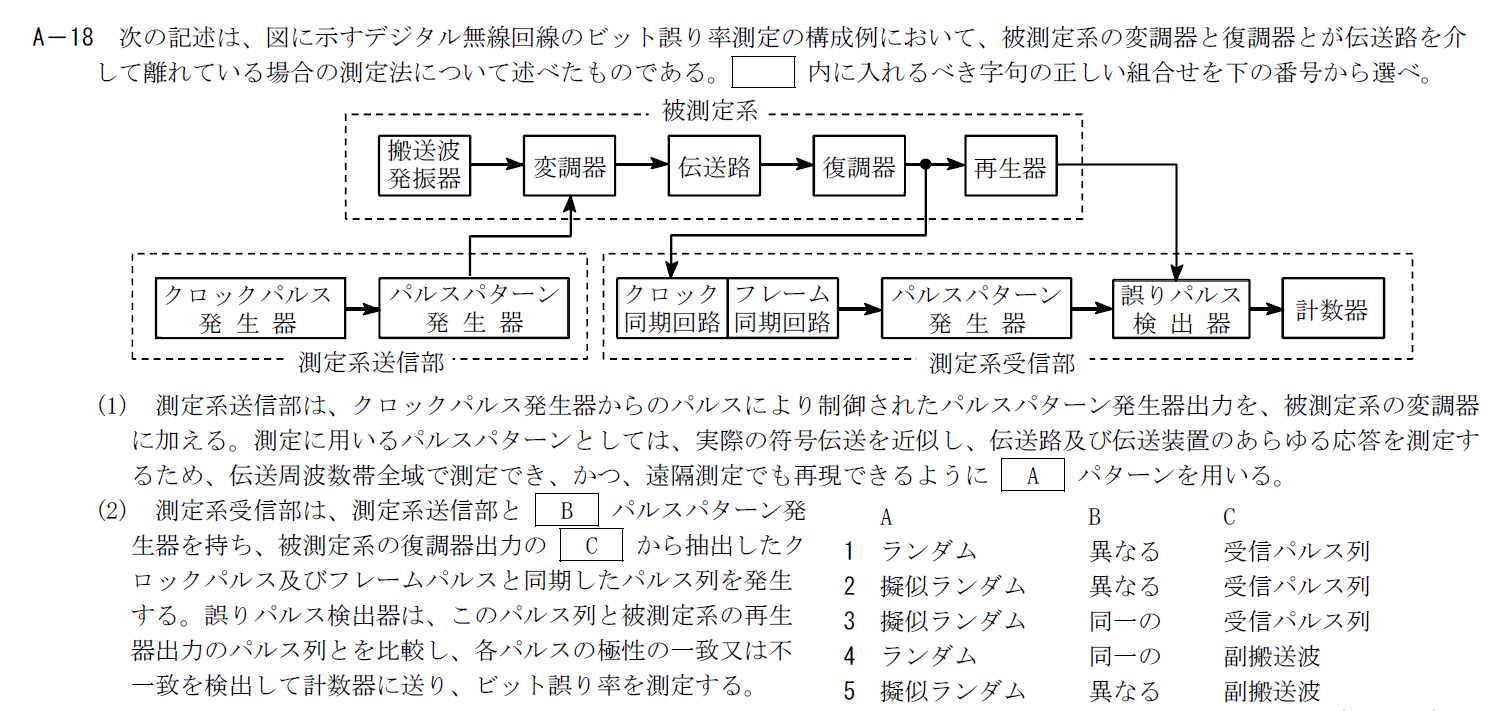
変調器と復調器が離れているときのビット誤り率測定に関する問題です。
A
完全なランダムパターンでは測定系受信部で再現することができないので疑似ランダムパターンを使用します。
そのため、Aには「疑似ランダム」が入ります。
B
測定系送信部と同一のパルスパターンを測定系受信部で再現して誤りの数を測定することでビット誤り率を測定します。
そのため、Bには「同一の」が入ります。
C
パルスパターンを比較するため、受信パルス列とパルスパターン発生器で生成したパルスパターンを同期させて一致・不一致を計数します。
そのため、Cには「受信パルス列」が入ります。
以上から答えは3です。
R.4.7 無線工学A(2回目) A-19
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-19
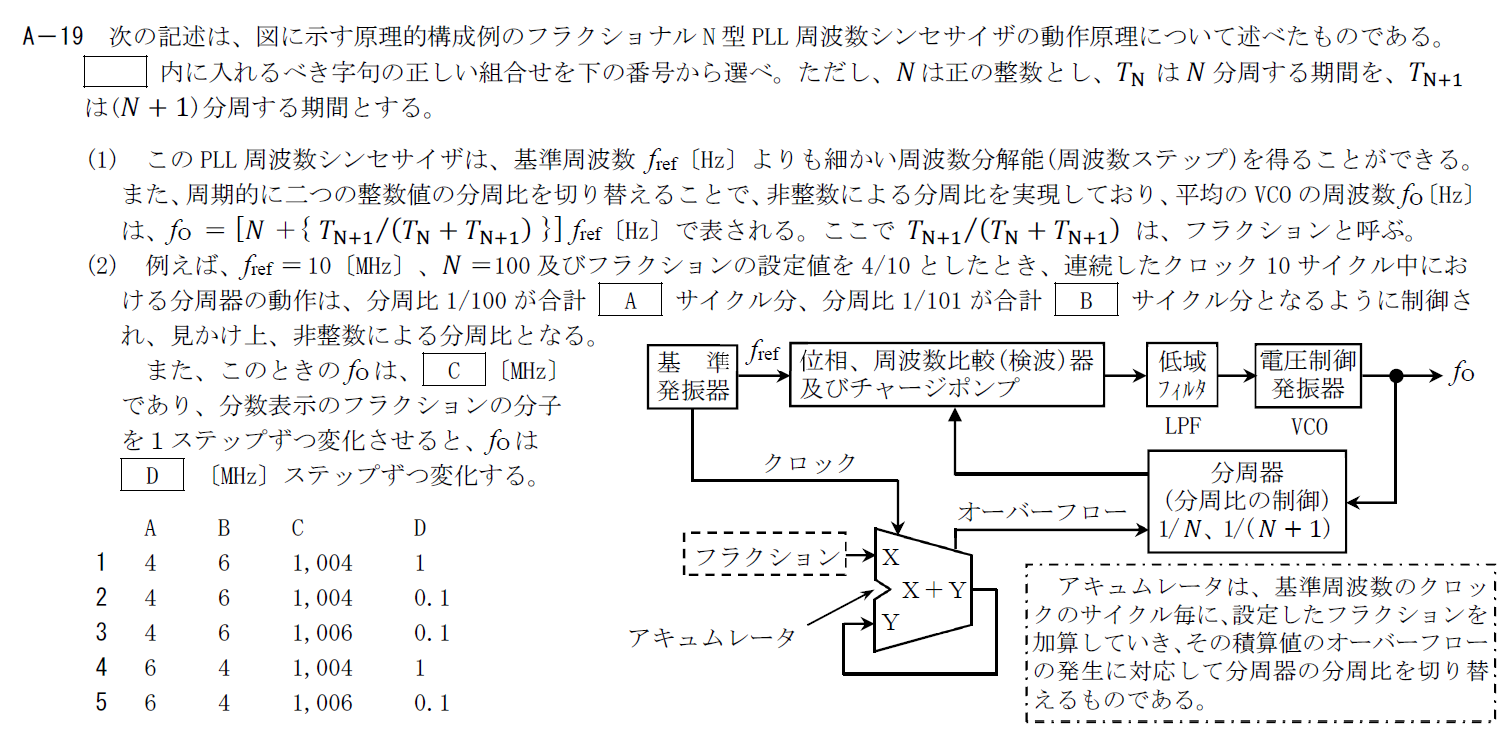
フラクショナルN型PLL周波数シンセサイザに関する問題です。
A,B
(2)でフラクションが4/10となっているので、計算すると \[ \frac{T_{N+1}}{T_N+T_{N+1}}=\frac{4}{10} \\ 10T_{N+1}=4T_N+4T_{N+1} \\ \frac{T_N}{T_{N+1}}=6/4 \] となります。
この結果から$T_N$と$T_{N+1}$の比が$6:4$です。
そのため、Aには「6」、Bには「4」が入ります。
C
$f_O$の計算式が与えられているので、 \[ f_O=\{ N+\frac{T_{N+1}}{T_N+T_{N+1}}\} f_{ref} \\ =(100+\frac{4}{10})\times 10 \times 10^6 \\ =1004[\rm{MHz}] \] となります。
そのため、Cは「1004」です。
D
フラクションの分母が10なので$10[\rm{MHz}]$の基準周波数を使うとフラクションの分子を1ステップ変化させると$f_O$は$1[\rm{MHz}]$ずつ変化します。
そのため、Dには1が入ります。
以上から答えは4です。
R.4.7 無線工学A(2回目) A-20

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-20
FFTアナライザに関する問題です。
A
FFTアナライザやスペクトラムアナライザでは周波数分解能と時間分解能はトレードオフの関係にあります。
そのため、周波数分解能を高くするためには時間分解能を下げる必要があります。
Aは「下げる」です。
B
被測定信号から適切に信号を切り取るのに使用するのは窓関数です。
そのため、Bには「窓関数」が入ります。
C
時間窓長はサンプリング周期×サンプリング点数となります。
そのため、Cは \[ T=N\Delta t \] です。
以上から答えは1です。
まとめ
令和4年7月の2回目の無線工学A A-16~20の問題を解説しました。 今回は問題の誘導に従っておけば解ける問題が多かったと思います。 このような問題は理屈が分かっていれば解けることも多いので問題をしっかり読んで落ち着いて解きましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント