【無線】1月の1陸技試験問題を解いてみた（R3.1 1回目　無線工学B A-1~A-5）

先月1陸技の試験が行われました。今更感がありますが、今年1月分の問題を解いてみたいと思います。 飽きるまでやります。

R.3.1 無線工学B（1回目） A-1

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R3年1月1回目　無線工学B A-1

2つの式の右辺を見ると、①はアンペアの法則、②はファラデーの法則だと分かります。 ①の右辺第2項に面食らうかもしれませんが、微視的なオームの法則です。 問題中ではこの項は答えに影響はしませんが電流密度の一部です。 何の式か分かれば

• A:rot \(H\)
• B:rot \(E\)
• C:変位電流

5が答えと分かるでしょう。

R.3.1 無線工学B（1回目） A-2

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R3年1月1回目　無線工学B A-2

この手の問題は消去法で解くのが良いでしょう。

1. 入力インピーダンスが一定の範囲が広いほど使用可能な周波数帯域幅が広いため正しい
2. 使用可能な周波数帯域が最も広いとき0Hz～fHzでと中心周波数はf/2なので200%を超えることはない。正しくない
3. 折返し半波長ダイポールは放射抵抗が半波長ダイポールより大きいので広帯域になるため正しい
4. ディスコーンアンテナはバイコニカルアンテナの1種なのでスリーブアンテナと比べると広帯域のため正しい
5. 対数周期アンテナは素子の長さで周波数帯域の上限と加減が決まるので八木アンテナより広いので正しい

なので答えは2です。

R.3.1 無線工学B（1回目） A-3

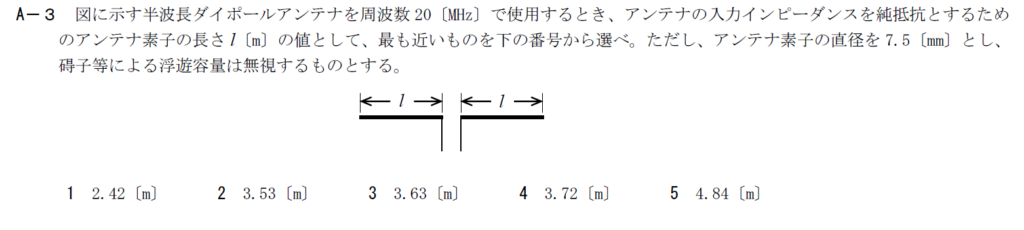
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R3年1月1回目　無線工学B A-3

真面目にやろうとすると計算がえげつないことになります。 半波長ダイポールのインピーダンスの虚部が42.55[Ω]です。 受信端開放単線式線路の特性インピーダンスが42.55[Ω]を打ち消すように短縮率\(\delta\)を決めればよいでしょう。 受信端開放単線式線路の特性インピーダンスは単線式線路の特性インピーダンス\(Z_0\)を使って次のように表せます。 \[ Z_l=-jZ_0\cot \beta l \] \(\beta=\frac{2\pi}{\lambda}\)、\(d\)は線路の直径、\(Z_0=138\log_{10} \frac{2l}{d}\)です。 短縮率が十分小さいとすれば、\(Z_l\simeq -jZ_0\pi \delta\)と表せます。 虚部がゼロになる短縮率\(\delta_0\)とすると\(\delta_0=\frac{42.55}{\pi Z_0}\)となります。 短縮率を無視して、\(l=\lambda/4\)として計算した\(\delta_0\)とし、それぞれの選択肢の短縮率と比較して近いものを選ぶのが速いでしょう。 一方定義に沿って求めた短縮率は\(\delta=1-\frac{4l}{\lambda}\)です。 計算すると\(\delta_0=0.0327\)です。 選択肢それぞれを検討してみましょう。5の選択肢は\(\lambda/4=3.75\)[m]に対して短縮できていないので論外です。

1. 0.355
2. 0.061
3. 0.032
4. 0.008

以上から答えは3となります。

R.3.1 無線工学B（1回目） A-4

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R3年1月1回目　無線工学B A-4

パラボラアンテナの利得\(G_I\)は開口率を\(\eta\)、直径を\(D\)[m]とすると \[ G_I=\eta \left(\frac{\pi D}{\lambda}\right)^2 \] です。 距離\(d\)[m]の地点の電力密度\(P_d[\rm{W/m^2}]\)は。 \[ P_d=\frac{G_IP_T}{4\pi d^2} \] です。 一方自由空間での電力密度は\(P_d=\frac{E^2}{120\pi}\)なので、 \[ E=\sqrt{120\pi\frac{G_IP_T}{4\pi d^2}}=\frac{\sqrt{30\times 240 \times \pi^2 \times 10}}{18\times 10^3}=47[\rm{mV/m}] \] だから答えは4。

R.3.1 無線工学B（1回目） A-5

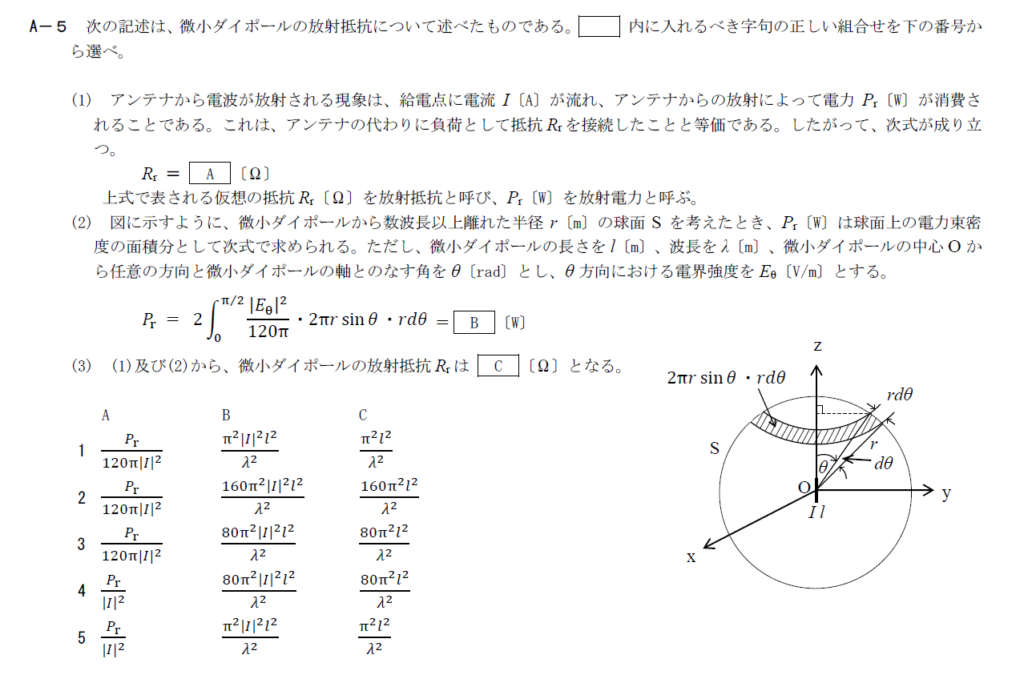
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R3年1月1回目　無線工学B A-4

\(P_r=|I|^2R_r\)なので(A)\(R_r=\frac{P_r}{|I|^2}\)です。 波長\(\lambda\)[m]、電流\(I\)[A]を長さ\(l\)[m]微小ダイポールに流すと最大放射方向で距離\(d\)[m]の電界強度\(E\)[V/m]は \[ E=\frac{60\pi I l}{\lambda d} \] で表せます。 ダイポールの8の字指向性はsinで表せるので \[ E_{\theta}=\frac{60\pi I l}{\lambda d}\sin\theta \] となります。 問題文中の積分に代入すると \[ P_r=\frac{120\pi^2|I|^2l^2}{\lambda^2}\int^{\frac{\pi}{2}}_0 \sin^3\theta d\theta=\frac{80\pi^2|I|^2l^2}{\lambda^2} \] となります（B）。 Aの結果にBの結果を代入すると(C)\(R_r=\frac{80\pi^2l^2}{\lambda^2}\)です 以上から答えは4となります。

まとめ

今回は令和3年1月1回目の1陸技の無線工学B最初の5問を解いてみました。 受かった人も来年頑張る人も気になっている問題もあったのではないでしょうか。 飽きるまで解いて記事にしていきたいと思います。

参考文献

勉強法 第一級陸上無線技術士の勉強法とおすすめ参考書

電磁気学をちゃんと学びたい人向け

上の難易度が高い人