令和7年1月の一陸技の試験の無線工学AのA-11~15の問題について解説します。
R.7.1 無線工学A A-11

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R7年1月 無線工学A A-11
GPSの搬送波位相を利用した干渉測位に関する問題です。
A
問題文から \[ (r+\Delta r)^2=r^2+d^2-2rd\cos \theta \] なので \[ r^2+2r\Delta r +\Delta r^2=r^2+d^2-2rd\cos \theta \\ 2r\Delta r=-2rd\cos \theta +d^2 -\Delta r^2 \\ \Delta r=-d\cos \theta +(d^2-\Delta r^2)/(2r) \\ \] となります。
\[ \vec{A}\cdot \vec{E}=d\cos \theta \\ |\vec{A}|^2=d^2 \] なのでこれを代入すると \[ \Delta r=-\vec{A}\cdot \vec{E}+(|\vec{A}|^2-\Delta r^2)/(2r) \] となります。
そのため、Aには「$-\vec{A}\cdot \vec{E}+(|\vec{A}|^2-\Delta r^2)/(2r)$」が入ります。
B
位相変化分の不確定性は1波長分になります。
L1の波長は19cmなのでBには「19」が入ります。
C
基準点と測位点が離れるほど遅延による影響が大きくなるので基線長は十分短くする必要があります。
そのため、Cには「短く」が入ります。
以上から答えは2です。
R.7.1 無線工学A A-12
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R7年1月 無線工学A A-12
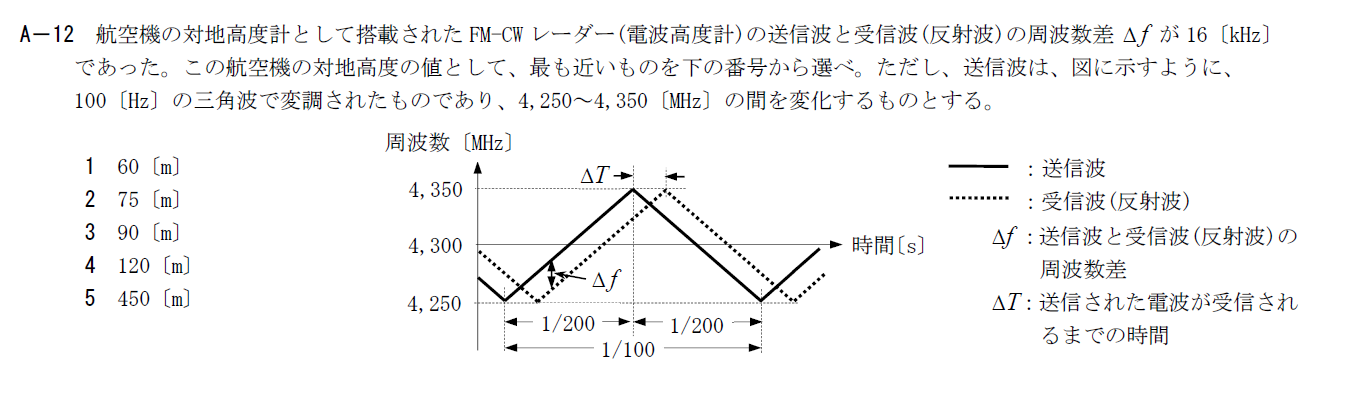
FM-CWレーダーによる測定結果から航空機の対地高度を計算する問題です。
この問題は同様の問題が令和4年7月1回目A-12で出題されています。
下記の記事も参考にしてください。

三角波の傾きは \[ \frac{100 \times 10^6}{1/200}=2 \times 10^{10}[\rm{Hz/s}] \] なので \[ \Delta T=\frac{\Delta f}{2 \times 10^{10}}=\frac{8}{10}\times 10^{-6} \\ =8 \times 10^{-7} \] です。
ここから航空機の対地高度を計算すると \[ h=c\Delta T/2 =3\times 10^8 \times 8 \times 10^{-7} \\ =120[\rm{m}] \] なので答えは4です。
R.7.1 無線工学A A-13
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R7年1月 無線工学A A-13
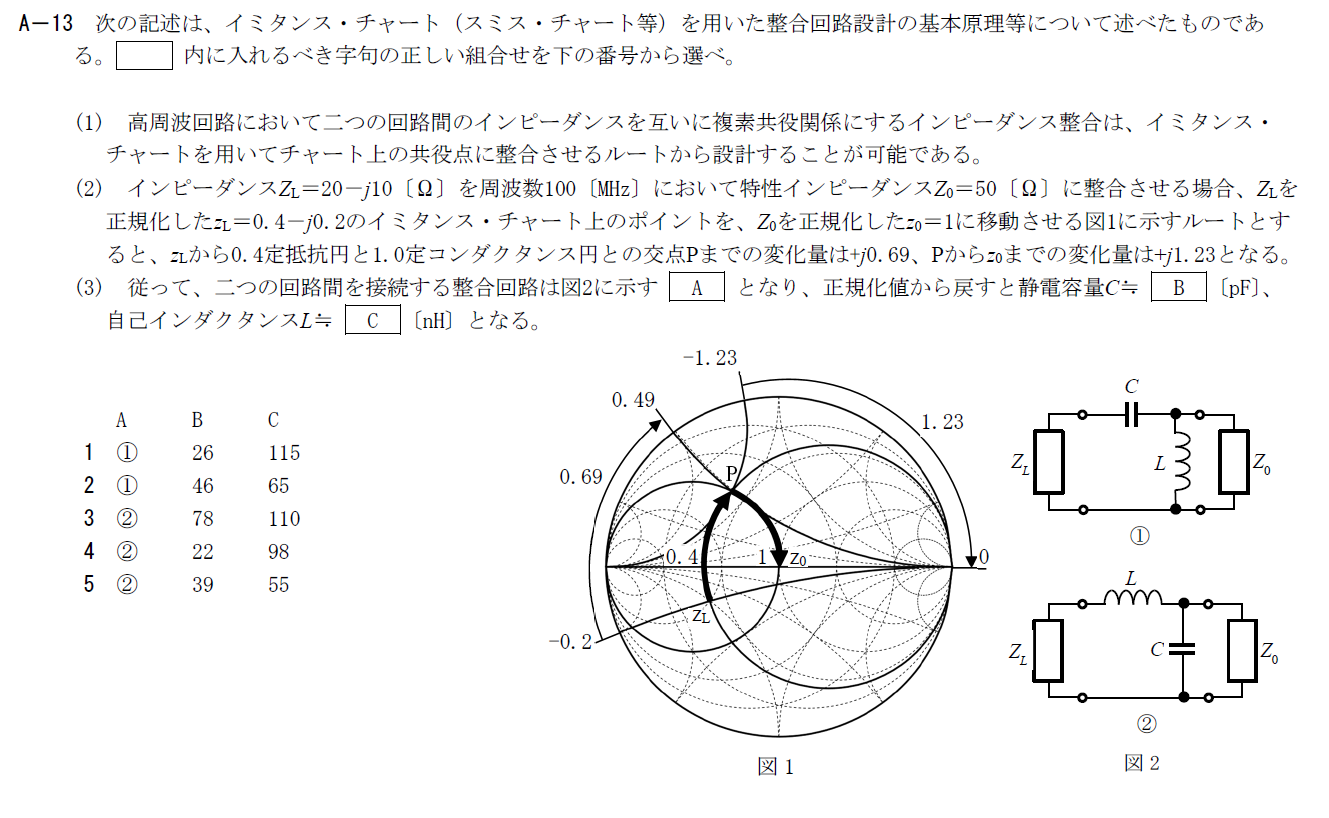
イミタンス・チャートに関する問題です。
この問題は同様の問題が令和5年1月2回目A-16で出題されています。
下記の記事も参考にしてください。

イミタンス・チャート上で整合をとる経路が違うので計算自体は違います。
A
$z_L\rightarrow P$では、スミス・チャートの定レジスタンス円を時計回りに移動しています
これは正のリアクタンスを直列につないだことを意味します。 つまり、$Z_L$にコイルを直列につなげます。
次に$P\rightarrow z_0$では定コンダクタンス円を時計回りに移動しています。
これは正のアドミッタンスを負荷に接続することを意味します。 つまり、$Z_L$にコンデンサを並列につなげます。
そのため、Aには②が入ります。
B
$P\rightarrow z_L$の変化量が$+j1.23$なので、 \[ j\omega C=\frac{j1.23}{Z_0} \\ C=\frac{1.23}{50 \times 2\pi \times 100 \times 10^6}=39.1 \times 10^{-12}\rm{[F]} \\ =39\rm{[pF]} \] となります。
C
$z_L\rightarrow P$の変化量が$+j0.69$なので、 \[ j\omega L=j0.69Z_0 \\ L=\frac{0.69 \times 50}{2\pi \times 100 \times 10^6}=54.9\times 10^{-9} \rm{[H]}\\ =55\rm{[nH]} \]
以上から答えは5です。
R.7.1 無線工学A A-14

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R7年1月 無線工学A A-14
衛星通信の回線設計に関する問題です。
この問題は同様の問題が令和5年7月1回目A-13で出題されています。
詳しい計算方法については下記の記事もご参照ください。

A
$1\rm{[W]}$は$0\rm{dBW}$なので、EIRPを計算すると \[ EIRP=0.0-5.0+2.0=-3.0\rm{[dBW]} \] となります。
そのためAには「$-3.0$」が入ります。
B
システム雑音温度をデシベルに直すと \[ T_S=10\log 300 =24.8\rm{[dBK]} \] なので、 \[ G/T=34.5-24.8-1.0=8.7\rm{[dB/K]} \] です。
そのため、Bには「$8.7$」が入ります。
C
\[ C/N_0=-3.0-171.6+8.7-(-228.6) \\ =62.7\rm{[dB]} \] なので、Cには「$62.7$」が入ります。
以上から答えは2です。
Cの計算が一番面倒くさく、AとBが分かれば答えは分かるのでCは必ずしも計算する必要はありません。 検算には使えますが、どの選択肢もCの値はAとBと矛盾しない値になっているので検算するあてになるかというと微妙です。 時間が余ったときに計算するくらいでもよいと思います。
R.7.1 無線工学A A-15
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R7年1月 無線工学A A-15
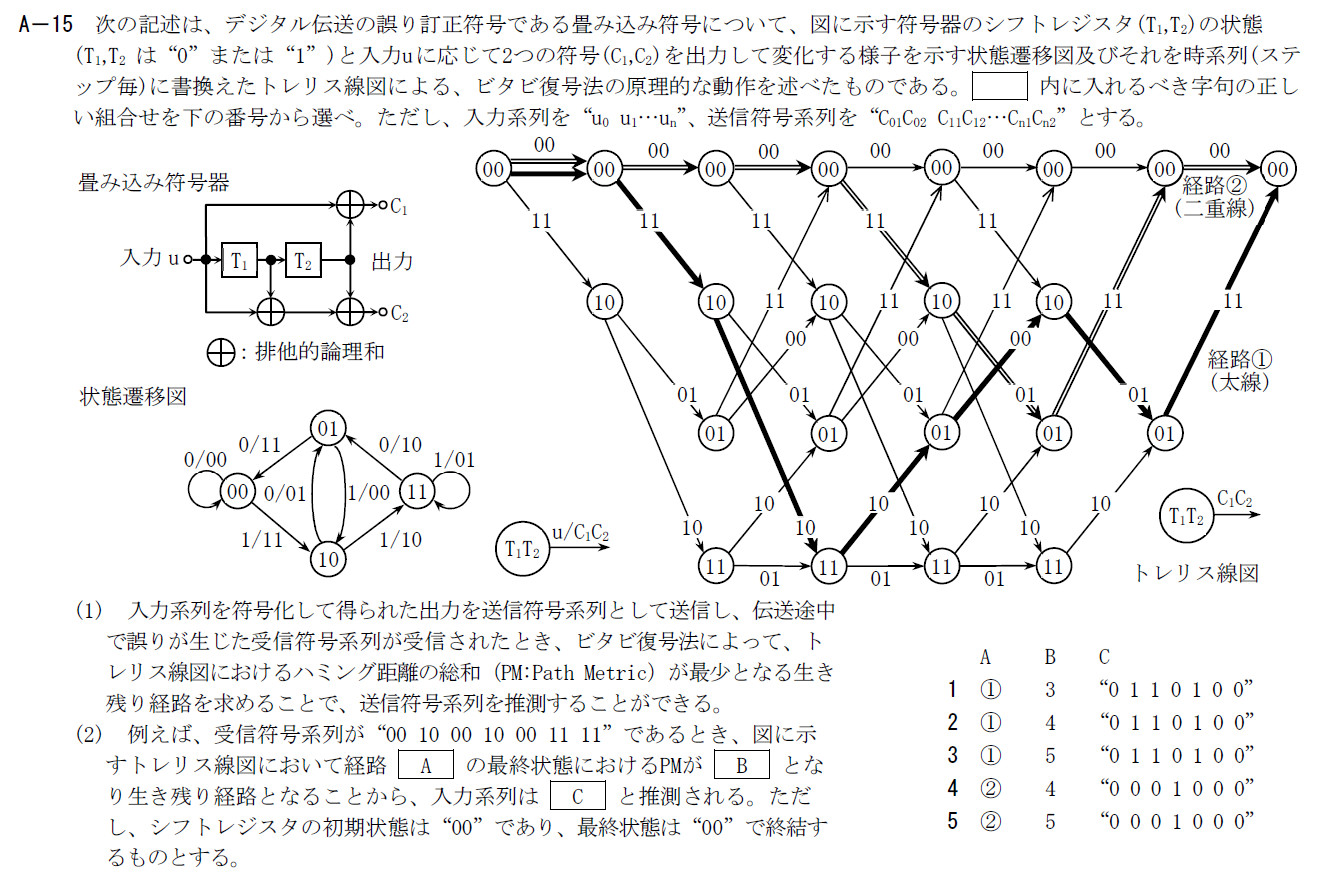
トレリス線図を使ったビタビ復号に関する問題です。
あまり見ない問題ですが、誘導に従えばそんなに難しくないです。
過去にはもっと単純な畳み込み符号器に関する問題は出題されています。 最近は同じ題材でも難易度が上がった問題が出題されているのが散見されます。
下記の記事も参考にしてください。
令和5年7月1回目A-15

令和4年1月2回目A-12

A,B
Aでは受信系列に最も近い生き残り経路を求めています。
本来は全経路を比較しますが、候補として2経路問題で与えられているのでそれぞれ計算しましょう。
| 系列 | PM | |
| 受信 | “00 10 00 10 00 11 11” | – |
| ① | “00 11 10 10 00 01 11” | 3 |
| ② | “00 00 00 11 01 11 00” | 5 |
となるのでPMが3の経路①が生き残り経路となります。
そのためAには「①」、Bには「3」が入ります。
C
経路①の出力から入力系列を状態遷移図に従って求めます。
シフトレジスタの初期値が”00″であり、①の系列の最初の2bitは”00″なので”00″→”00″に遷移するのは入力が”0″の時です。
そのため、最初の入力は”0″と分かります。
同様の方法で以降も入力を求めていくと入力は下記のようになります。
“0 1 1 0 1 0 0”
以上から答えは1です。
まとめ
令和7年1月の無線工学Aの試験A-11~A-15の問題について解説しました。 特に無線工学Aでは新傾向の問題や少し難易度を挙げたような問題が増えてきたように思います。 初めて見る問題でもしっかり誘導がついていて、問題自体は対して難しくないことも多いです。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント