令和5年1月の1陸技の試験2回目の無線工学AのB-1~5の問題について解説します。
R.5.1 無線工学A(2回目) B-1
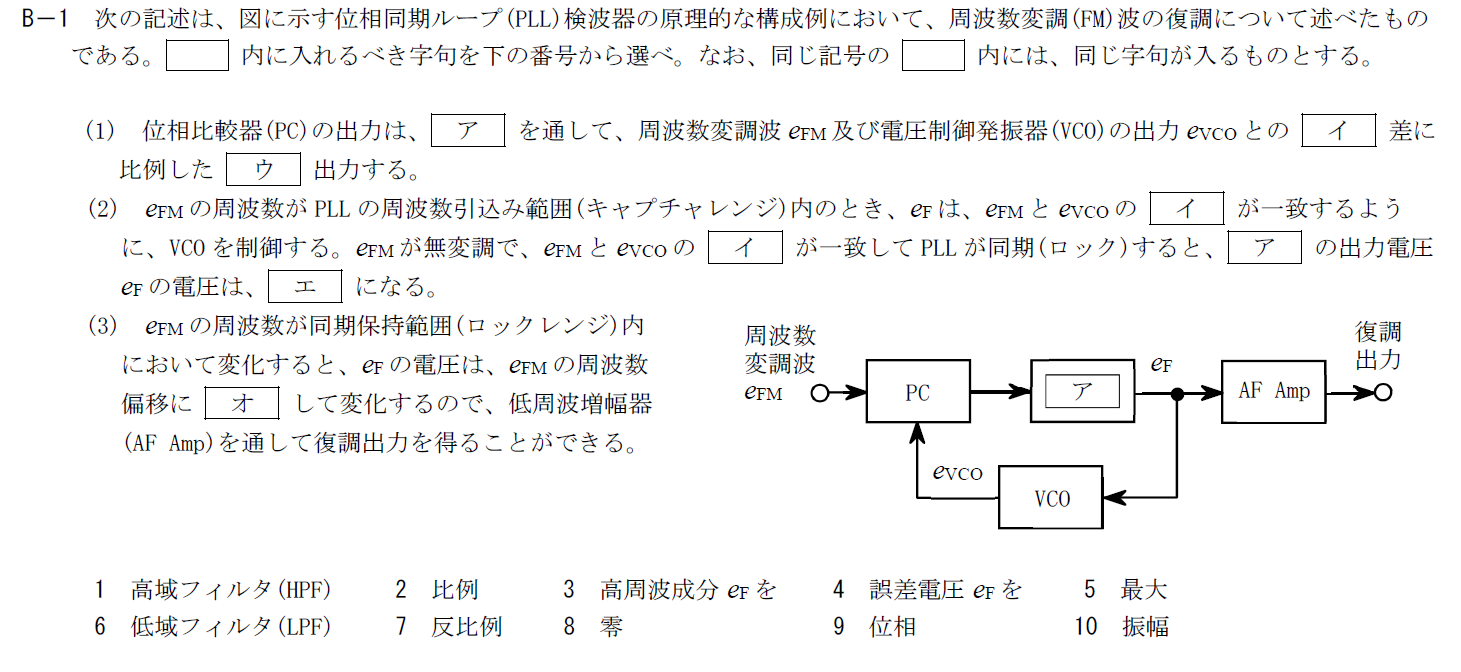
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A B-1
位相同期ループ(PLL)検波器に関する問題です。
同じ問題文の問題が令和4年1月1回目のA-6で出題されています。
下記の記事もご参照ください。

ア
図については上記の問題と同じなので同じ位置を見てください。
復調出力の周波数は変調波の周波数に対して十分低いので、低域フィルタ(LFP)を入れるのが適切と考えるとよいでしょう。
以上から、アには6.「低域フィルタ(LPF)」が入ります。
イ,ウ
ここは令和4年1月1回目のA-6の(1)と同じ文となっています。
考え方については上記記事を参照してください。
イには9.「位相」、ウには4.「誤差電圧$e_F$を」が入ります。
エ
エの空欄は令和4年1月1回目のA-6のCと同じです。
エには8.「零」が入ります。
オ
ここは令和4年1月1回目のA-6の(3)と同じ文です。
位相比較器(PC)では$e_{FM}$と$e_{VCO}$の位相差に比例した電圧を出力します。
そのため、オには2.「比例」が入ります。
R.5.1 無線工学A(2回目) B-2

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A B-2
アイパターンについての正誤問題です。
ア
アの記述はアイパターンの定義の通りなので正しい記述です。
そのため、アは正しいので答えは1です。
イ
アイパターンといってもオシロスコープの出力の1種類なので、横軸は時間、縦軸が振幅となっています。
つまり、横方向のずれ幅は時間軸方向の変動を意味します。
そのため、イは正しいので答えは1です。
ウ
縦軸の開きはHighとLowの振幅差です。 その差が大きいほど振幅の変動に対する余裕度が大きいことを意味します。
そのため、ウは正しいので答えは1です。
エ
アイパターンは信号のHightとLowを重ね合わせて表示したものです。
これは複数数のデータが同時に表示されなければならないので発生頻度の低い現象は一般的な事象に隠れて観測が難しいです。
そのため、エは誤っているので答えは2です。
オ
図のアイパターンの振幅はHghとLowの2値しか表示されていないので4値NRZ符号ではなく、2値NRZ符号のアイパターンです。
そのため、オは誤っているので答えは2です。
R.5.1 無線工学A(2回目) B-3

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A B-3
デジタルフィルタに関する問題です。
ア、イ
伝達関数の周波数特性を振幅と位相で明示的に書き下すと、 \[ H(e^{j\omega })=|H(e^{j\omega })|\theta (\omega ) \] となります。
ここで$|H(e^{j\omega })|$は振幅特性、$\theta (\omega )$は位相特性を表します。
そのため、アには2.「振幅特性」、イには6.「位相特性」が入ります。
ウ
インパルス応答が有限長のシステムをFIR(Finite Impulse Response)システムといいます。
そのため、ウには8.「FIR」が入ります。
エ
ウとは逆にインパルス応答が無限長のシステムをIIR(Infinite Impulse Response)システムといいます。
そのため、エには3.「IIR」が入ります。
オ
選択肢の中でインパルス応答の打ち切りによる不連続性から発生する現象はギブス現象です。
FIRにおけるギブス現象は周波数特性が振動する現象です。
ドプラ現象は波源や観測者が移動することで観測される周波数が変化する現象、ルンゲ現象は数値解析で発生する現象です。
以上から、オには9.「ギブス」がはいります。
R.5.1 無線工学A(2回目) B-4
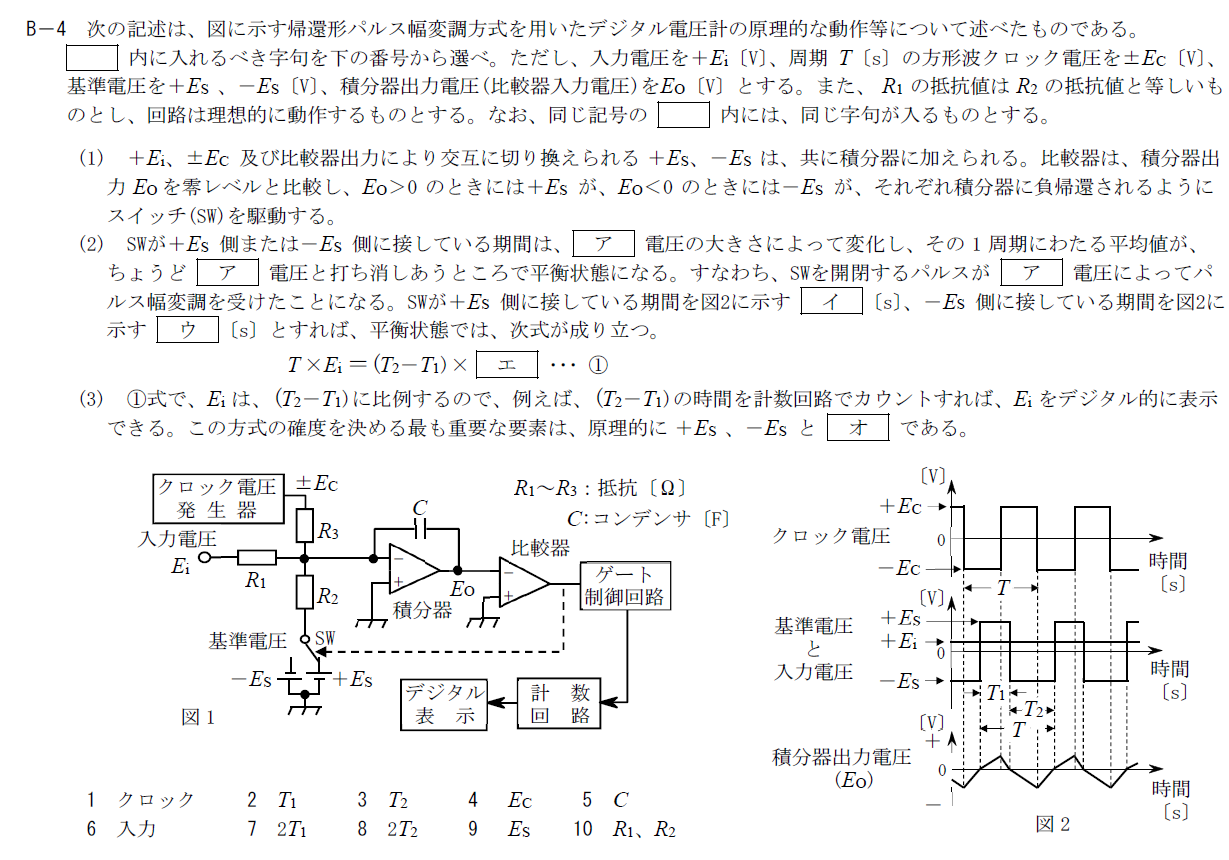
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A B-4
デジタル電圧計の原理に関する問題です。
同じ問題文の問題が令和4年1月2回目のA-18で出題されています。
下記の記事もご参照ください。

ア
この空欄は令和4年1月2回目のA-18のAの空欄と同じです。
そのため、アには6.「入力」が入ります。
イ、ウ
イとウの空欄は図2の中段から読み取れます。
$+E_S$の時間が$T_1$、$-E_S$の時間が$T_2$となっています。
そのため、イには2.「$T_1$」、ウには3.「$T_2$」が入ります。
エ
①の式は令和4年1月2回目のA-18の式を簡単にしたものが記載されています。 式は下記の通りで、これは入力電圧の平均値とSWに接している電圧の平均値が平行していることを表しています。 \[ \frac{E_iT}{CR_1}+\frac{E_ST_1}{CR_2}-\frac{E_ST_2}{CR_2}=0 \]
この式を使う方が分かりやすいのでこれを変形します。 \[ T\times E_i=(T_2-T_1)\frac{R_1}{R_2}E_S \] 問題文から$R_1=R_2$なので、エには9.「$E_S$」が入ります。
オ
エの式において$\frac{R_1}{R_2}$が精度よく分かれば精度よく測定できます。
そのため、オには10.「$R_1, R_2$」が入ります。
R.5.1 無線工学A(2回目) B-5

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A B-5
振幅変調波に関する問題です。
ア
$e$を計算してみましょう。 \[ e=(A+B\cos pt)\cos \omega t \\ =A\cos \omega t +B\cos pt \cos \omega t \\ =A\cos \omega t +\frac{B}{2}\cos (\omega +p)t +\frac{B}{2}\cos (\omega -p)t \]
アの空欄は2行目の式に相当します。
そのため、アには8.「$A\cos \omega t +B\cos pt \cos \omega t$」が入ります。
イ
イは変調度の定義です。
\[ m=(B/A)\times 100\rm{[\%]} \]
そのため、イには4.「$(B/A)$」が入ります。
ウ
アで記載した式の通りで、搬送波を表す$A\cos \omega t$の項は変化しません。
そのため、ウには10.「変わらない」が入ります。
エ
変調度が50%なので、それぞれの側波帯の電圧は$\frac{A}{4}$となります。
電力は電圧の2乗に比例するので電力は$1/16$倍となります。
そのため、エには2.「$1/16$」が入ります。
オ
変調度が100%の時はピーク時の振幅が搬送波の振幅の2倍になるので電力は4倍です。
そのため、オには6.「$4$」が入ります。
まとめ
今回は令和5年1月の無線工学A(2回目)の試験B-1~B-5の問題について解説しました。 B問題は出題形式に関わらず過去問が多く出題されます。弊サイトも活用して事前に対策することで得点源としてしまいましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント