令和4年7月の1陸技の試験1回目の無線工学AのA-1~5の問題について解説します。
R.5.1 無線工学A(1回目) A-1
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学A A-1
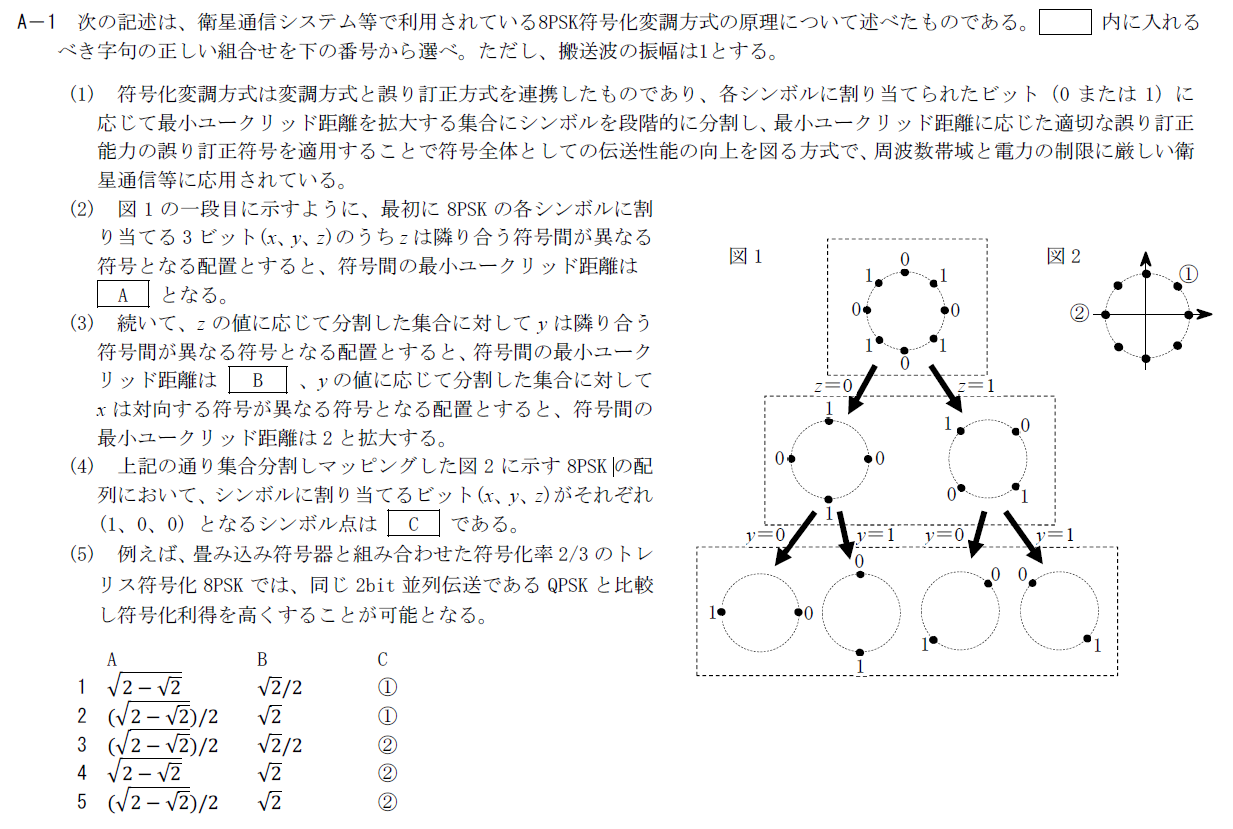
8PSK符号化変調方式の原理に関する問題です。
文章は長いですが、誘導に従えばそれほど難しくありません。
A
符号間の最小ユークリッド距離は点同士の最小距離です。 図1の一段目の図を見て、隣あった点を考えればよいことになります。 隣あった2点と円の中心を結んだ三角形は頂角$pi/4$、等辺の長さが1の二等辺三角形となります。
符号間の最小距離を$r$として、この二等辺三角形に余弦定理を使うと \[ 1+1-2\cos \frac{\pi}{4}=r^2 \\ r=\sqrt{2-\sqrt{2}} \] となります。
B
二段目についても同様に考えてると、頂角が$\pi/2$の直角二等辺三角形になります。 そのため、Bには$\sqrt{2}$が入ります。
C
$(x,y.z)=(1,0,0)$に従って、図1を上からたどると、②の位置になります。
以上から答えは4です。
R.5.1 無線工学A(1回目) A-2
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学A A-2
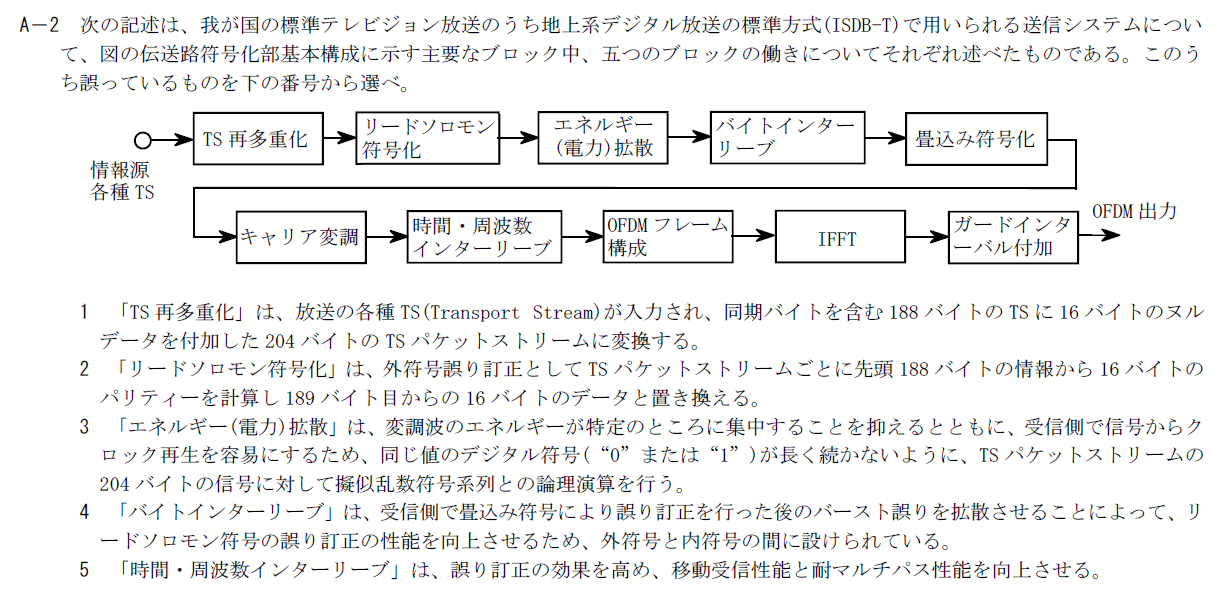
地上系デジタル放送の標準方式(ISDB-T)に関して誤った選択肢を選ぶ問題です。
誤った選択肢は3です。
エネルギー(電力)拡散はスロットの先頭1バイト(同期バイト)を除く203バイトに対して行われます。
そのため、答えは3です。
R.5.1 無線工学A(1回目) A-3

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学A A-3
2つの単一正弦波による振幅変調波の電力を計算する問題です。
この問題は令和4年1月2回目A-2で類題が出題されています。
求めるものが違いますが計算式は同じものが使えます。 下記の記事をご参照ください。

記事内の計算式を使うと \[ P_m=P_c(1+\frac{m_1^2}{2}+\frac{m_2^2}{2}) \\ P_c=\frac{P_m}{1+m_1^2/2+m_2^2/2}=\frac{15.84}{1+\frac{72}{625}+\frac{128}{625}}=12.0\rm{[kW]} \] となります。
以上から答えは3です。
R.5.1 無線工学A(1回目) A-4

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学A A-4
FM波の占有周波数帯域幅に関する問題です。
ベッセル関数が出てきて少し難しそうに見えるかもしれませんが、問題文を読めばそれほど難しくはありません。 公式を覚えておくとすぐ解けますが、真面目に解くと計算が面倒くさいので場合によっては後回しにした方がいいかもしれません。
ここでは公式を使って簡単に答えを求めた後、別解として真面目に解いてみることにします。
変調信号の周波数を$f_p$、最大周波数変移を$\Delta F$とします。
公式を使った解法
一般に占有周波数帯域幅$B$は次のように表されます。 \[ B=2(f_p+\Delta F) \] この公式は占有周波数帯域幅に入る側帯波の数が多い時に成り立つ近似式であることは頭の片隅にでも入れておきましょう。
この公式に当てはめると \[ B=2(10+40)=100\rm{[kHz]} \] となります。
側帯波は変調信号の周波数間隔で発生するので、片側だけで見れば次数$n$は$n=50/10=5$となります。
以上から答えは4です。
真面目に計算する解法
表を使って真面目に計算しましょう。
まず変調指数を求めます。 \[ m=\frac{\Delta F}{f_p}=4 \] ここから与えられた表の$J_n^2(4)$の列を見ればいいことが分かります。
占有周波数帯域幅は全電力の99%が含まれる帯域幅と定義されます。 側帯波の電力は第一種ベッセル関数の2乗値に比例するのでこの和が0.99を越える時の次数$n$が占有周波数帯域幅に含まれる側帯波の次数の最大値です。
$n=4$までの和 \[ J_0^2(4)+2\sum^4_{n=1}J_n^2(4) =0.9597 \] $n=5$までの和 \[ 2J_0^2(4)+2\sum^5_{n=1}J_n^2(4)=0.9945 \] となるので、$n=5$となります。
5次の側帯波までが占有周波数帯域に含まれるので占有周波数帯域幅は$2\times 5\times f_p=100\rm{[kHz]}$となります。
R.5.1 無線工学A(1回目) A-5

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学A A-5
直交周波数分割多重(OFDM)方式の復調の原理に関する問題です。
誘導に従って計算していきましょう。
A
(2)の$S_{BI}(t),S_{BQ}(t)$式をそのまま①式に代入します。 \[ u(t)=\sum^{N-1}_{n=0}\{a_n\cos \omega_n t-b_n\sin \omega_n t\}+j\{a_n\sin \omega_n t+b_n\cos \omega_n t\} \\ =\sum^{N-1}_{n=0}(a_n+b_n)(\cos \omega_nt+j\sin\omega_nt) \] ここで$\omega_n=2\pi nf_s$です。
答えの選択肢を展開した方が速いかもしれません。
以上からAには「$(a_n+b_n)(\cos \omega_nt+j\sin\omega_nt)$」が入ります。
B
オイラーの公式から \[ \cos \omega_nt+j\sin\omega_nt=e^{j\omega_nt} \] なので、$t=\frac{k}{Nf_s}$とすると \[ e^{j(2\pi nk)/N} \] です。
以上からBには「$j(2\pi nk)/N$」が入ります。
C,D
②の形は逆離散フーリエ変換の形なのでCには「逆離散フーリエ変換」が入ります。
上記の通り、$d_n$を求めるためには離散フーリエ変換すればいいです。 そのため、Dには「離散フーリエ変換」が入ります。
E
逆フーリエ変換の定義にそのまま当てはめればいいので、 \[ d_n=\frac{1}{N}\sum^{N-1}_{k=0}u(\frac{k}{Nf_s})e^{-j(2\pi nk)/N} \] となります。
そのため、Eには「$-j(2\pi nk)/N$」が入ります。
以上から答えは1です。
まとめ
今回は令和5年1月の無線工学A(1回目)の試験A-1~A-5の問題について解説しました。 知識だけでなく問題に書いてある内容を利用して解くタイプの問題も多く出題されています。 ぱっと見難しそうに見えますが、落ち着いて解いていきましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント