令和5年7月の1陸技の試験1回目の無線工学BのA-1~5の問題について解説します。
R.5.7 無線工学B(1回目) A-1

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-1
マクスウェル方程式に関する問題です。
この問題については令和4年1月2回目A-1と同じで、式①と②の順番が逆転しています。 こちらの記事をご参照ください。

答えは
- A:$\nabla \times$
- B:ファラデー
- C:アンペア
- D:変位電流
のため、答えは3です。
R.5.7 無線工学B(1回目) A-2

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-2
電波の空間分布の性質に関する問題です。
同様の問題が令和3年7月2回目A-4で出題されています。
この問題は令和4年1月2回目A-1と問題文が同じで空欄の位置が違います。 内容的には同じなので下記の記事を参考にしてください。

答えは5です。
R.5.7 無線工学B(1回目) A-3
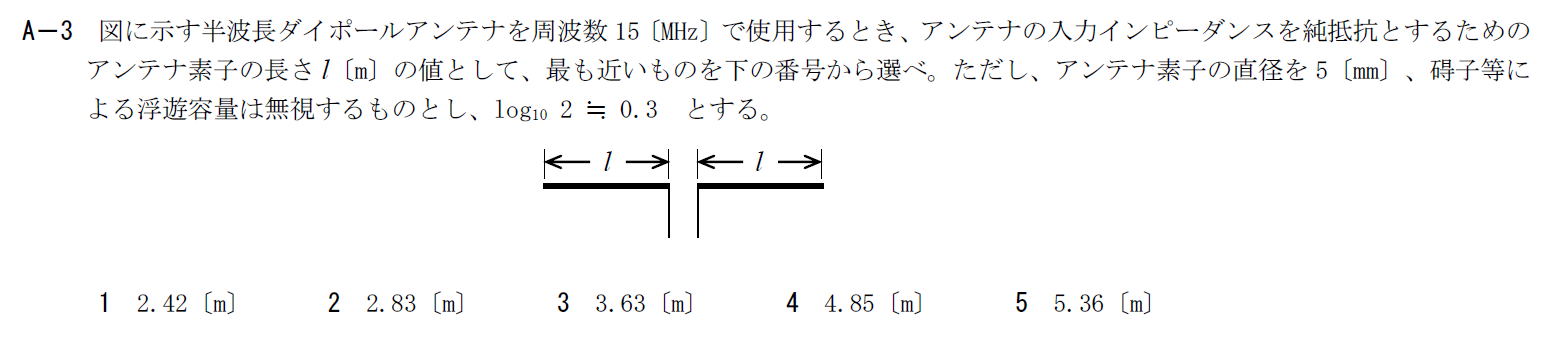
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-3
半波長ダイポールアンテナのインピーダンスを純抵抗にするための条件を求める問題です。
この問題は令和3年1月1回目A-3や令和4年1月2回目A-5で同様の問題が出題されています。
解き方については下記の記事をご参照ください。

また、使っている計算式の導出については下記で触れています。

アンテナの入力インピーダンスは \[ Z_0=138\log_{10}\frac{2L}{d}=455.4[\rm{\Omega}] \] です。 この結果を短縮率$\delta$の式に代入すると \[ \delta =\frac{42.55}{\pi Z_0}=0.03 \] となります。
そのため、 \[ l=L(1-\delta)=4.85\rm{[m]} \] となります。
以上から答えは4です。
同様の問題は使用する周波数の1/4波長より少し短い値の選択肢を選んでおけばまず正解できる問題です。 計算する時間がたりない時は短縮率3%くらいになる選択肢を選んでおきましょう。
R.5.7 無線工学B(1回目) A-4

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-4
円形パラボラアンテナの利得を計算する問題です。
円形パラボラアンテナの利得(dB)は \[ G=10\log_{10}\eta \left(\frac{\pi D}{\lambda}\right)^2 \] と表せます。 ここで、$\eta$は開口効率、$D$はパラボラアンテナの開口径です。
問題の値を代入すると \[ G=10\log_{10}0.8\times \left(\frac{\pi \times 2}{0.025}\right)^2 \\ =10\log_{10}(0.8\times \pi^2 \times 2^2 \times 40^2) \\ =47\rm{[dB]} \] となります。
以上から答えは2です。
R.5.7 無線工学B(1回目) A-5

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-5
アンテナの可逆定理(相反定理)に関して誤った選択肢を選ぶ問題です。
この問題は令和4年1月1回目A-3で同様の問題が出題されています。
下記の記事もご参照ください。

誤った選択肢は2です。
相反定理からアンテナは送受信で指向性は同じです。
以上から答えは2です。
まとめ
今回は令和5年7月の無線工学B(1回目)の試験A-1~A-5の問題について解説しました。 過去問との類題も多く、弊サイトでも網羅できている問題も多かった印象です。 これ以降の問題では少し見慣れない問題もありましたので、そちらについては詳しく解説していきたいと思います。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント