令和4年1月の1陸技の試験1回目の無線工学BのA-16~20の問題について解説します。
R.4.1 無線工学B(1回目) A-16

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-16
F層での反射による伝搬の計算問題です。
半波長ダイポールから放射された電波の距離$d$離れた点での電界強度の式を使って適切な計算ができるかという問題となっています。
まず、電波が伝搬する経路を考えましょう。
電離層で反射された電波はちょうど送受信点の中点上空の電離層を通っています。
すると、送信点から反射点までの距離と反射点から受信点までの距離はいずれも500[km]です。
そのため、電波の伝搬距離は1000[km]です。
反射時に第二種減衰しますが、最後に計算するため、ここでは考えません。
半波長ダイポールアンテナから距離$d[\rm{m}]$離れた点での電界強度は$E=\frac{7\sqrt{P}}{d}$です。
この式は素直に覚えておくのがいいでしょう。
$P=10[\rm{kW}], d=1000[\rm{km}]$を代入すると、$E=700[\rm{\mu V/m}]$となります。
デシベルに直すと$20\log_{10} E=57[\rm{dB\mu V}]$です。
最後に第二種減衰の$6[\rm{dB}]$を引けば、$E=51[\rm{dB\mu V}]$となります。
以上から、答えは3です。
R.4.1 無線工学B(1回目) A-17

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-17
MIMOに関する問題です。
この問題には明らかに誤った選択肢があります。
答えは5です。
MIMOは送受信それぞれ複数のアンテナを使って複数の伝送路で通信する方式です。
もちろんその伝送路の中に垂直偏波の伝送路も存在し得ます。(使わない場合もあります)
MIMOで垂直偏波を用いることができないわけではありません。
R.4.1 無線工学B(1回目) A-18
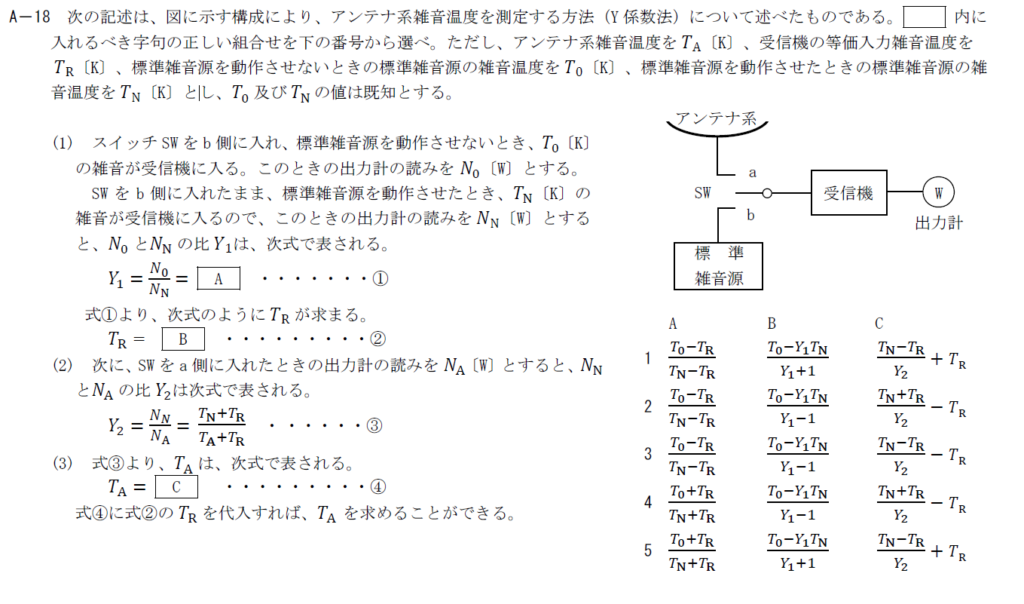
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-18
雑音温度の測定法に関する問題です。
A
出力計には標準雑音源と受信機の雑音の合計が読みとして表示されるので、$N_0 \propto (T_0+T_R)$となります。
$N_N$についても同様なので、$Y_1=\frac{N_0}{N_N}=\frac{T_0+T_R}{T_N+T_R}$となります。
原理的には③式と同じ格好の式となるはずなのでわからなければ③の式を参考にしましょう。
B
①の式を$T_R$について解くと
\[
T_R=\frac{T_0-Y_1T_N}{Y_1-1}
\]
となります。
C
③の式を$T_A$について解けば
\[
T_A=\frac{T_N+T_R}{Y_1}-T_R
\]
となります。
以上から答えは4です。
R.4.1 無線工学B(1回目) A-19

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-19
マイクロ波測定に関する問題ですが、どちらかというとフリスの伝達公式が分かっているかを問う問題と思ったほうがとっつきやすいかもしれません。
A
フリスの伝達公式から$P_r=\left( \frac{\lambda }{4\pi d}\right)^2G_1G_2P_t$なので、
\[
P_r/P_t=\left( \frac{\lambda}{4\pi d}\right)^2G_1G_2
\]
です。
そのため、Aには$\frac{\lambda}{4\pi d}$が入ります。
B
$G_1=G_2=G$として①式に代入してみましょう。
\[
P_r/P_t=\left( \frac{\lambda}{4\pi d}\right)^2G^2 \\
G^2=\left( \frac{4\pi d}{\lambda}\right)^2P_r/P_t \\
G=\frac{4\pi d}{\lambda}\sqrt{P_r/P_t}
\]
となります。
そのため、Bには$\frac{4\pi d}{\lambda}\sqrt{P_r/P_t}$が入ります。
C
アンテナが1つの時は反射板を使って、反射板の反対側の同じ距離に同一のアンテナがあるとみなして同じ計算ができます。
そのため、Cには「反射板」が入ります。
以上から、答えは2です。
R.4.1 無線工学B(1回目) A-20

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-20
開口アンテナの利得測定においてアンテナの大きさに起因する誤差に関する問題です。
これも2つの波源からの経路差による位相差を考える2波モデルのような問題に帰着します。
A
まず、$R_2$に当たるルートの中を計算してみましょう。
問題文から$D_1+D_2<< R_1 $なので、
\[
R_2=\sqrt{R_1^2+\left(\frac{D_1}{2}+\frac{D_2}{2} \right)^2} \\
\simeq R_1\left\{1+\frac{1}{2}\left( \frac{D_1+D_2}{2}\right)^2\right\} \\
=R_1 +\frac{(D_1+D_2)^2}{8R_1}
\]
です。
$\Delta R$の式に代入して、$\Delta R=\frac{(D_1+D_2)^2}{8R_1}$です。
B
ここでの計算は前回のA-14の問題でやったような2はモデルと同じようなことを考えます。

アンテナ1内の任意の2点から放射された電波のアンテナ2の任意の点のでの位相差を$\phi$とすると
\[
E=E_0|1+e^{j\phi}|=2E_0\cos\frac{\phi}{2}
\]
です。ここで$E_0$は受信される電界の大きさです。
誤差がない(位相差$\phi=0$)の時の電界強度は$2E_0$なので、利得の測定誤差$\delta$は受信される電界の大きさです。
\[
\delta =(1-\frac{E}{2E_0})
\]
最大誤差が2%($\delta=0.02$)なので$\cos \frac{\phi}{2}=0.98$です。
ここから$\phi$を求めるのが正攻法ですが、この計算が試験の場でできる人はそう多くないでしょう。
$\phi =\frac{2\pi}{\lambda}\Delta R$です。
選択肢には$\lambda/4$と$\lambda/16$しかないため代入してみたほうが早いです。
仮に$\Delta R=\lambda/4$だとすると$\phi =\pi/2$となるので、$\cos \frac{\phi}{2}=\frac{\sqrt{2}}{2}$となり、0.98とは程遠い値になります。
消去法でBに入るのは$\lambda/16$です。
関数電卓でちゃんと計算すると正しいことがわかります。
C
$\Delta R=\frac{\lambda}{16}$なので、Aの結果から$R_1=\frac{2(D_1+D_2)^2}{\lambda}$です。
以上から答えは1です。
まとめ
先日行われた令和4年1月1回目の1陸技の無線工学BのA-16~20を解いてみました。
同じ試験の中にも同様の解き方ができる問題が出ることもあります。
最後までどうしても解けない問題があったら他の問題を見てみるとヒントになることがあるかもしれません。
ひらめくことができるように基礎的な内容は道筋だけでも頭に入れておくと便利です。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人

コメント