令和3年7月の1陸技の試験2回目の無線工学AのA-1~5の問題について解説します。
R.3.7 無線工学A(2回目) A-1
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学A A-1
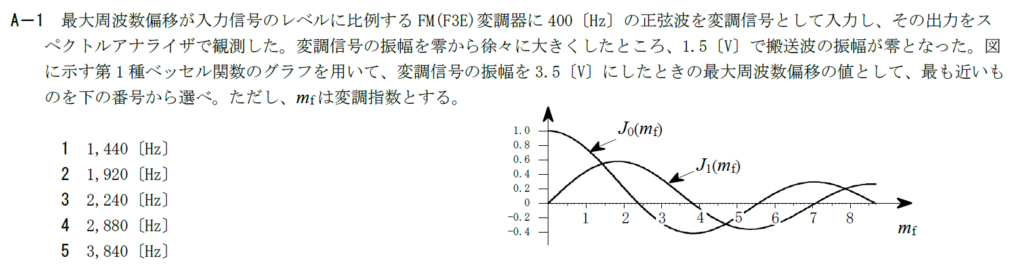
FMの最大周波数偏移を第一種ベッセル関数から求める問題です。
搬送波成分は$J_0(m_f)$に比例します。 FMの変調指数は$m_f=\frac{\Delta F}{f_p}$で表せます。 $\Delta F$は最大周波数偏移、$f_p$は信号波周波数です。
$\Delta F$は信号波の電圧に比例するので$\Delta F=kV_p$と表せます。
$m_f=\frac{\Delta F}{f_p}=\frac{kV_p}{f_p}=k’V_p$とおきましょう。
グラフから$V_p=1.5[\rm{V}]$の時、$m_f=2.4$なので$k’=8/5$となります。
計算すると$\Delta F=kV_p=k’f_pV_p=2240[\rm{Hz}]$となるため、答えは3です。
R.3.7 無線工学A(2回目) A-2

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学A A-2
地上系デジタル方式の標準テレビジョンの圧縮方式に関する問題です。
A
動き補償予測符号化では原信号とフィールド信号の差と動き量のみを送ることで伝送する情報量を減らします。 原信号とフィールド信号の和を送信しても情報量は増えるだけです。
そのため、Aには差が入ります。
B
人間の視覚は高い周波数に対して鈍感なので、この周波数成分を間引いても問題ありません。
そのため、Bには高いが入ります。
C,D
発生頻度の高い符号に短いビット列を割り当てることで伝送する情報量を減らせます。 アルファベットのモールス信号にも同様の手法が使われています。
そのため、Cには高い、Dには低いが入ります。
以上から答えは4です。
R.3.7 無線工学A(2回目) A-3

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学A A-3
変調信号の周波数を$f_m$、位相変調指数を$m_p$とすると$F_d=f_mm_p$となります。
位相変調指数の誤差±20%なので、$F_d$の計算には20%分大きな値を使います。 そのため、$F_d=f_mm_p\times1.2=48[\rm{kHz}]$です。
あとは与えられた式から$B_w=2(f_m+F_d)=296[\rm{kHz}]$となります。
そのため、答えは4です。
R.3.7 無線工学A(2回目) A-4
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学A A-4
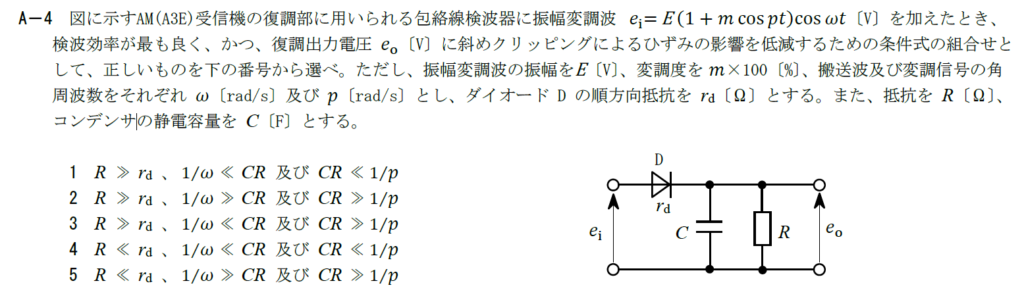
包絡線検波の斜めクリッピングひずみ(ダイアゴナルクリッピングひずみ)に関する問題です。
斜めクリッピングひずみは包絡線検波回路の応答が信号の変化に対して遅れることにより発生します。 そのため、周波数の高い搬送波に対しては応答を遅くし、変調信号に対しては十分な応答速度を確保する必要があります。
応答速度は時定数$CR$によって決まるので$CR>>1/\omega ,CR << 1/p$とすればよいことになります。 ダイオードでの減衰は小さくする必要があるので$R >> r_d$とします。
以上から、答えは1です。
R.3.7 無線工学A(2回目) A-5

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学A A-5
非線形増幅回路の出力に含まれる周波数成分の振幅を計算問題です。
すべてを愚直に計算しても良いですが、試験時間もあるので、$2\omega_1-\omega_2$の周波数成分が含まれる項に辺りをつけて計算するのがいいでしょう。
問題で求められているのは$2\omega_1-\omega_2$です。 三角関数の加法定理を考えると3つの三角関数の積の形$\sin ^2\omega_1t\sin \omega_2t$に比例する項からこの周波数成分が出てくると予想することができます。
この項は$e_i^3$に比例する項に含まれます。
入力$e_i$は$e_i=A\sin \omega_1t +B\sin \omega_2t$と書けるので \[ e_i^3=A^3\sin^3\omega_1t +3A^2B\sin^2\omega_1t\sin\omega_2t+3AB^2\sin \omega_1t\sin^2 \omega_2t+B^3\sin^3\omega_2t \] となります。
最初に予想した$\sin ^2\omega_1t\sin \omega_2t$に比例する項があります。
これを計算してみましょう。 \[ 3A^2B\sin^2\omega_1t\sin\omega_2t=3A^2B\frac{1}{2}\left\{ (1-\cos 2\omega_1t)\sin\omega_2t\right\} \\ =\frac{3}{2}A^2B\left\{ \sin \omega_2t-\frac{1}{2}\sin (2\omega_1+\omega_2)t+\frac{1}{2}\sin (2\omega_1-\omega_2)\right\} \\ =\frac{3}{2}A^2B\sin \omega_2t -\frac{3}{4}a^2B\sin (2\omega_1+\omega_2)t +\frac{3}{4}A^2B\sin (2\omega_1-\omega_2) \] 第3項が求めたい周波数成分です。
出力は$a_3e_i^3$なので、振幅は$3a_3A^2B/4$となり、答えは4です。
まとめ
今回は令和3年7月1回目の1陸技の無線工学AのA-1~5を解いてみました。 過去問が多く出題される1陸技の試験ですが、ここ最近は1回の試験で2回分の過去問が出るので過去問もはかどりますね。 次の試験を目指すならこの時期からであれば次の試験まで十分に時間が取れます。 1陸技を目指す方は頑張っていきましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人


コメント