令和4年7月の1陸技の試験、無線工学Aの2回目のA-1～5の問題について解説します。
R.4.7 無線工学A（2回目） A-1
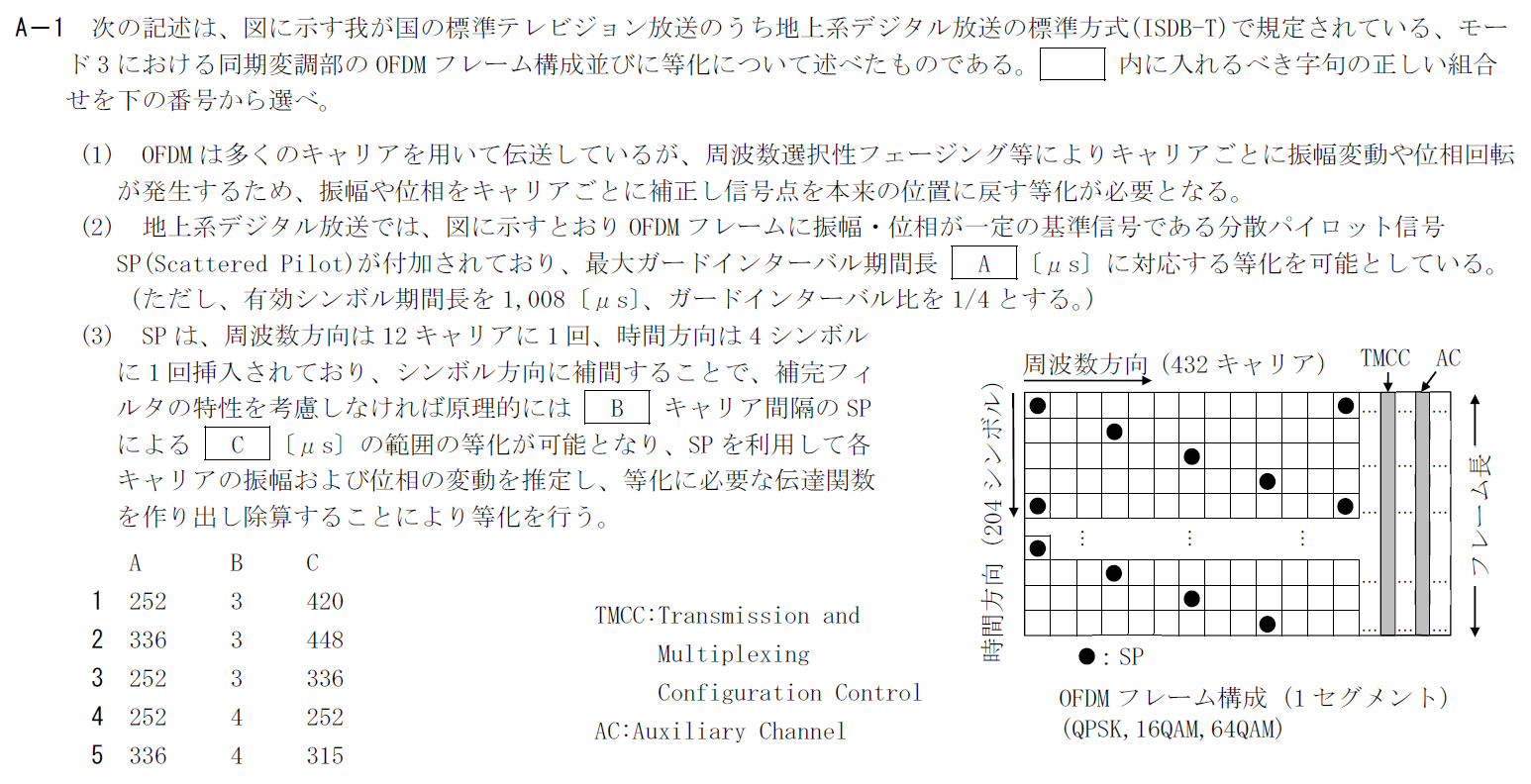
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-1
地上系デジタル放送の標準方式(ISDB-T)に関する問題です。
A
(2)はガードインターバルに関しての文です。
ガードインターバル比は有効シンボル期間長に対するガードインターバルの時間の比です。
そのため、計算すると
\[
1008/4=252[\rm{\mu s}]
\]
となります。
そのため、Aには「252」が入ります。
B
与えられた図を周波数方向に見ると3キャリアごとにSPがあることが分かります。
そのため、Bには「3」が入ります。
C
3キャリア間隔でSPがあるので、原理的には有効シンボル長の1/3の範囲の等価が可能です。
\[
1008/3=336[\rm{\mu s}]
\]
となるので、Cには「336」が入ります。
以上から答えは3です。
R.4.7 無線工学A（2回目） A-2
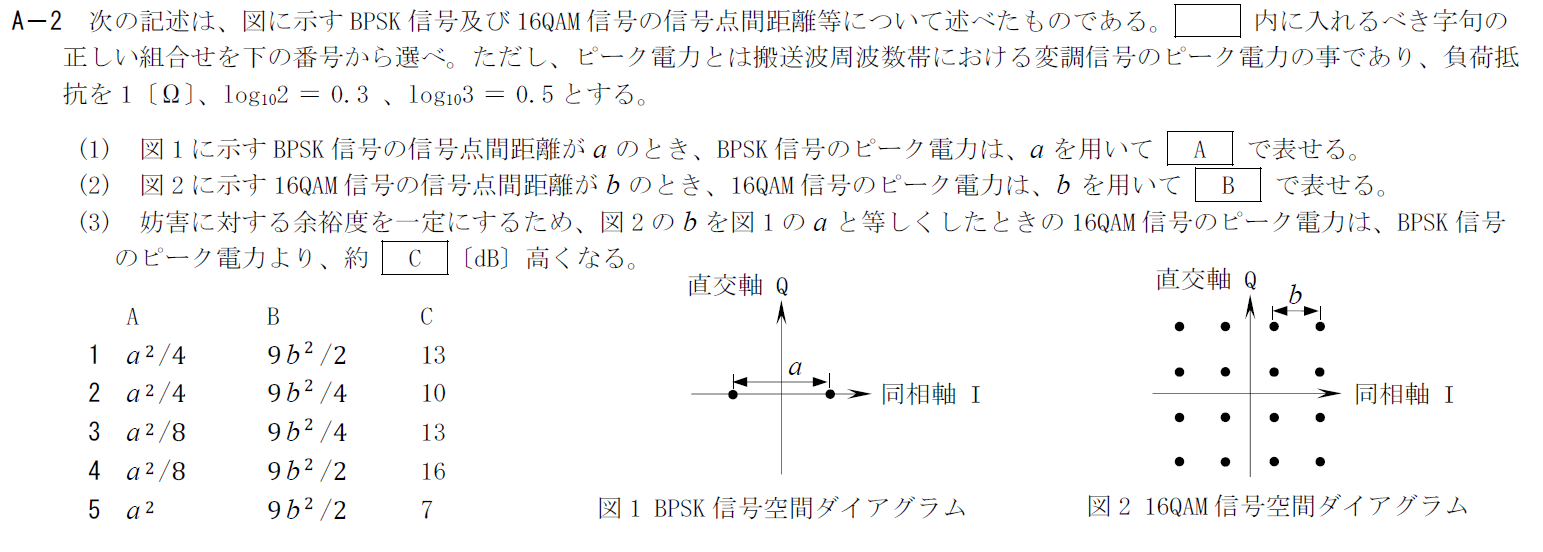
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-2
BPSK信号と16QAMの信号点間距離や妨害に対する強さに関する問題です。
最初に一般論を考えておきましょう。
信号のI成分を$u_I(t)$、Q成分を$u_Q(t)$とすると変調波$A(t)$は
\[
A(t)=u_I(t)\cos 2\pi f_ct +u_Q(t)\sin 2\pi f_ct
\]
と表されます。
$(u_I(t),u_Q(t))$が信号空間ダイアグラム上の点を表します。
信号の振幅を$R(t)$、位相を$\theta (t)$とすると
\[
u_I(t)=R(t)\cos \theta (t) \\
u_Q(t)=R(t)\sin \theta (t)
\]
です。
この時、電力$P$は
\[
P=\bar{A^2(t)}=\frac{1}{2}(\bar{u_I^2(t)}+\bar{u_Q^2(t)})
\]
となります。
$\bar{a}$は$a$の集合平均操作を表します。
A
BPSKでは
\[
u_I(t)=\frac{a}{2} \\
u_Q(t)=0
\]
となります。
これを電力の式に代入すると$P=a^2/8$となります。
そのため、Aには「$a^2/8$」が入ります。
B
16QAMの電力がピークになるときは原点から一番遠い点に対応するので
\[
u_I(t)=\frac{3b}{2} \\
u_Q(t)=\frac{3b}{2}
\]
です。
上記の条件で電力を計算すると$P=9b^2/4$となります。
そのため、Bには「$9b^2/4$」が入ります。
C
$b=a$の時のBPSKと16QAMのピーク電力の比がCに入ります。
この比を計算すると18となります。
これをデシベルに直すと
\[
10\log 18=10(2\log 3+\log 2) =10+3=13
\]
となります。
この結果からCには「13」が入ります。
以上から答えは3です。
R.4.7 無線工学A（2回目） A-3
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-3
FSKの変調方式に関する問題です。
A
第2項の積分を計算すると次のようになります。
\[
\int^T_0[\cos \{ 2\pi (f_1-f_2)+\phi_1 -\phi_2\}]dt \\
=\frac{1}{2\pi (f_1-f_2)}[\sin 2\pi (f_1-f_2)t]^T_0 \\
=\frac{1}{2\pi (f_1-f_2)}\sin 2\pi (f_1-f_2)T
\]
この結果が0になる条件は、$\sin$の中身が$\pi$の整数倍になればいいので
\[
2\pi (f_1-f_2)T =n\pi
\]
となります。
そのため、Aには「$n\pi$」が入ります。
B
$n=1$の時、変調指数は0.5となります。
これが直行条件を満足する変調指数の最小値となり、0と1の周波数差が最も小さくなるので、周波数スペクトルの広がりが最も小さくなる変調指数です。
そのため、Bには「0.5」が入ります。
C
ガウスフィルタをかけることはすなわち、帯域を制限することになるので、狭帯域化が図れることを意味します。
そのため、Cには「狭帯域化」が入ります。
以上から答えは4です。
R.4.7 無線工学A（2回目） A-4
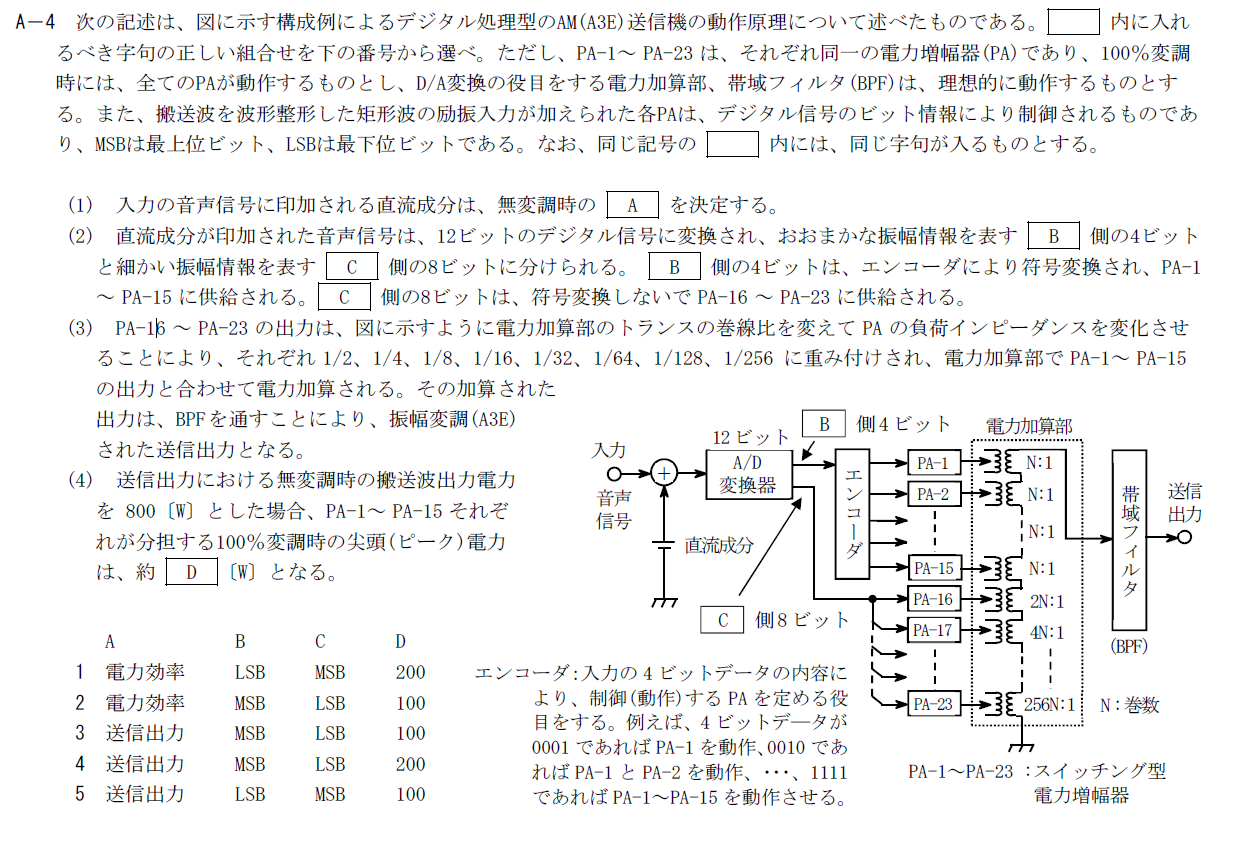
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-4
デジタル処理型のAM送信機の原理に関する問題です。
A
音声信号に印可される直流成分は無変調時の送信電力を決定します。
電力効率はPAや電力加算部の効率によって決定されます。
そのため、Aには「送信電力」が入ります。
B, C
デジタル処理型のAM送信機では、少ないビットで大まかな情報を、残りのビットで細かい振幅を表現します。
音声信号の12ビット中MSB側4ビットをおおまかな振幅情報、LSB側8ビットを細かい振幅の表現に使用します。
そのため、Bには「MSB」が、Cには「LSB」が入ります。
D
変調度100%の時、振幅のピークが無変調時の2倍になるので、尖頭電力は無変調時の4倍です
このことか尖頭電力は3200[W]です。
PA-1~15の重みは1倍、PA-16~23は1/2~1/256で合計約1倍となります。
そのため、尖頭電力全体を16等分した電力200[W]がPA-1~15がそれぞれ分担する電力といえます。
そのため、Dには「200」が入ります。
以上から答えは4です。
R.4.7 無線工学A（2回目） A-5
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-5
二乗検波に関する計算問題です。
内容的には令和3年7月(1回目)のA-4を一般化した内容となっています。
検波電流を計算してみましょう。
\[
i=k e^2 \\
=kA^2(1+m\sin pt)^2\sin^2 \omega t \\
=kA^2(1+m\sin pt)^2\frac{1}{2}(1-\cos 2\omega t) \\
=\frac{kA^2}{2}(1+m\sin pt)^2-\frac{kA^2}{2}(1+m\sin pt)^2\cos 2\omega t
\]
第一項が信号波成分、第二項が変調波の第二高調波成分を表します。
信号波に関する問題なので第一項を考えることにします。
\[
\rm{(第一項)}=\frac{kA^2}{2}+kA^2m\sin pt +\frac{kA^2m^2}{2}\sin^2 pt \\
=\frac{kA^2}{2}+kA^2m\sin pt +\frac{kA^2m^2}{2}\frac{1}{2}(1-\cos 2pt) \\
=\frac{kA^2}{2}(1+\frac{m^2}{2})+kA^2m\sin pt +\frac{kA^2m^2}{4}\cos 2pt
\]
第一項は直流成分、第二項は信号波成分、第三項は信号波の第二高調波成分となります。
この係数を見ると
- 信号波：$kA^2m$
- 第二高調波：$kA^2m^2/4$
となります。
以上から答えは2です。
まとめ
令和4年7月の1回目の無線工学A A-1~5の問題を解説しました。
面倒な計算問題も多く出題されています。
この解説ではできるだけ丁寧に計算するようにしていますが、試験前に慣れておいて、試験時には暗算するくらいの気持ちでいるのがいいと思います。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人
コメント