R.4.7 無線工学A(1回目) A-1
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月1回目 無線工学A A-1
A
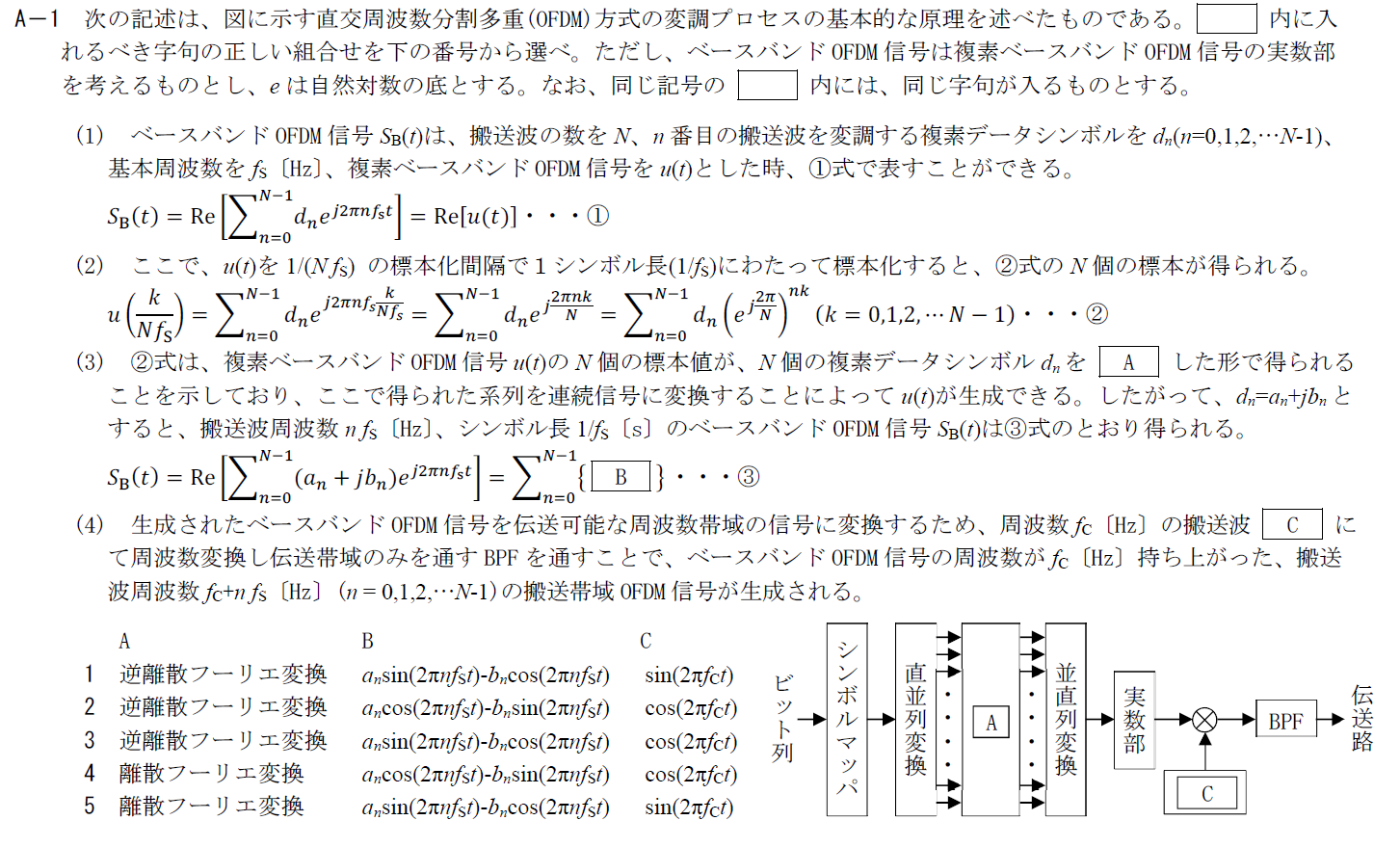
OFDMの送信側では各搬送波の振幅・位相の情報を逆離散フーリエ変換により時間軸の波形に変換し、それを送信周波数に周波数変換して送信します。 ここでは送信側の変調について述べられているので、Aには「逆離散フーリエ変換」が入ります。B
Bには$\Sigma$の中の実部が入ります。 $e^{j2\pi nf_st}$をオイラーの公式で展開して計算すれば \[ (a_n+jb_n)\{\cos (2\pi nf_st)+j\sin (2\pi nf_st)\} \\ =a_n\cos 2\pi nf_st-b_n\sin 2\pi nf_st+j\{a_n\sin (2\pi nf_st)+b_n\cos (2\pi nf_st)\} \] となります。 Bにはこの実部が入るので「$a_n\cos (2\pi nf_st)-b_n\sin (2\pi nf_st)$」が入ります。C
搬送波も$e^{j2\pi f_ct}$の実部が入るのでCには「$\cos (2\pi nf_ct)$」が入ります。 以上から答えは2です。R.4.7 無線工学A(1回目) A-2

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月1回目 無線工学A A-2
R.4.7 無線工学A(1回目) A-3
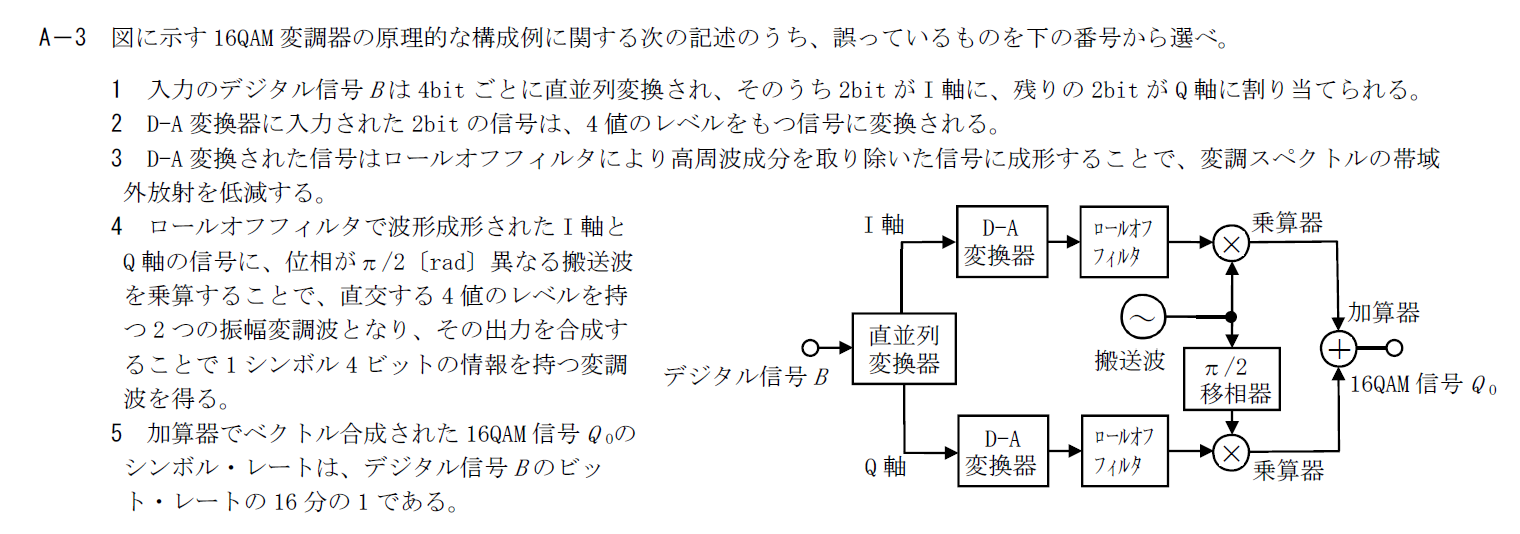
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月1回目 無線工学A A-3
R.4.7 無線工学A(1回目) A-4
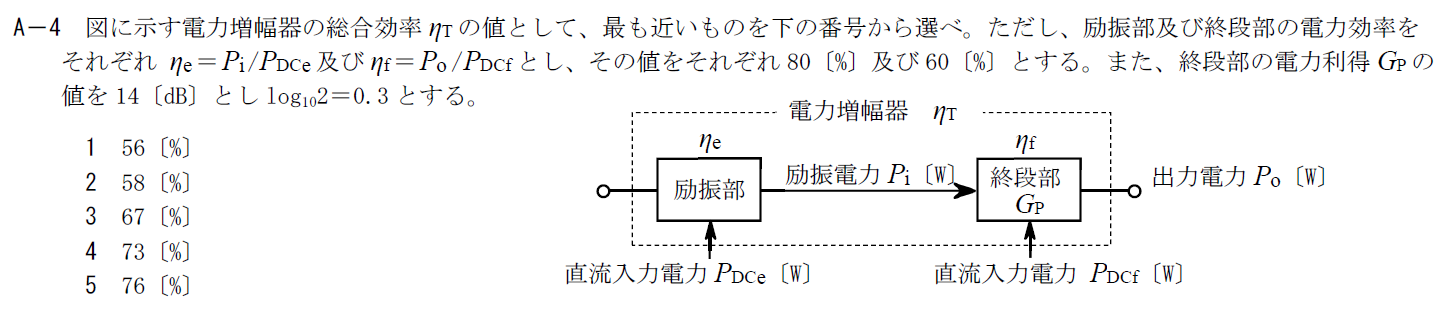
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月1回目 無線工学A A-4
R.4.7 無線工学A(1回目) A-5
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月1回目 無線工学A A-5
A
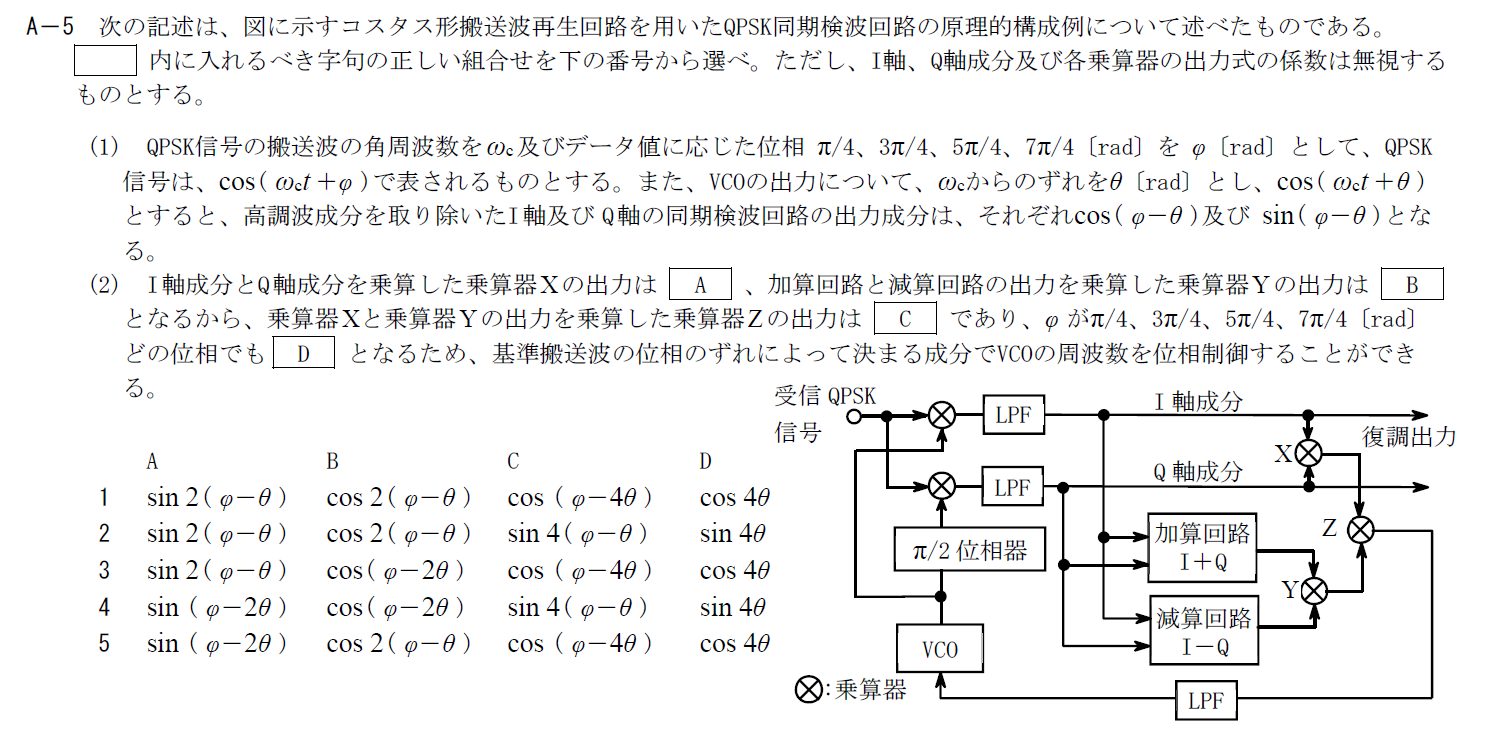
Xの乗算器には$\cos (\phi -\theta)$と$\sin (\phi -\theta)$が入力されます。 これらを乗算すると \[ \sin (\phi -\theta)\cos (\phi -\theta)=\frac{1}{2}\sin 2(\phi -\theta) \] です。 係数は無視するのでAには「$\sin 2(\phi -\theta)$」が入ります。B
乗算器Yには加算器と減算器の出力が入力されるのでYの出力は \[ \{\cos (\phi -\theta)+\sin (\phi -\theta)\}\{\cos (\phi -\theta)-\sin (\phi -\theta)\}=\cos^2(\phi -\theta)-\sin^ (\phi -\theta) \\ =\frac{1}{2}\{1+\cos 2(\phi -\theta)\}-\frac{1}{2}\{1-\cos 2(\phi -\theta)\} \\ =\cos 2(\phi -\theta) \] です。 以上からBには「$\cos 2(\phi -\theta)$」が入ります。C
Zの出力はAとBの答えの積なのでAの時の計算と同様に倍角の公式を使えば \[ \sin 2(\phi -\theta)\cos 2(\phi -\theta)=\frac{1}{2}\sin 4(\phi -\theta) \] となります。 そのため、Cには「$\sin 4(\phi -\theta)$」が入ります。D
$\phi =\pi /4, 3\pi /4, 5\pi /4,7\pi /4$の時、$4\phi =(2n-1)\pi$となります。ここで$n=1,2,3,4$です。 ここでZの出力を考えると \[ \sin 4(\phi -\theta)=\sin (-4\theta + \pi)=-\sin(-4\theta)=\sin(4\theta) \] となります。 そのため、Dには「$\sin(4\theta)$」が入ります。 以上から答えは2です。まとめ
少し間が空きましたが令和4年7月の1回目の無線工学A A-1~5の問題を解説しました。 システムの方式に関する問題は覚えてないと解けない問題もあるのでしっかり対策をしておきましょう。 三角関数の公式は覚えている必要はないですが、試験会場で求められるようにしておくのも重要です。 勉強法 第一級陸上無線技術士の勉強法とおすすめ参考書参考文献
リンク
電磁気学をちゃんと学びたい人向け
リンク
上の難易度が高い人
リンク
リンク



コメント