令和4年7月の1陸技の試験2回目の無線工学BのA-1~5の問題について解説します。
R.5.1 無線工学B(2回目) A-1

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学B A-1
自由空間内の電波の偏波に関する問題です。
この問題については令和3年7月2回目A-1と同じで、CとDのみ逆転しています。 こちらの記事をご参照ください。

答えは
- A:$\pi/2$
- B:$\pi$
- C:円
- D:直線
のため、答えは1です。
R.5.1 無線工学B(2回目) A-2

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学B A-2
半波長ダイポールアンテナと微小ダイポールアンテナによる電界強度の比を求める問題です。
同様の問題が令和3年7月2回目A-3で出題されています。
計算方法については下記の記事をご参照ください。 $E_1$と$E_2$の関係が逆転しているので注意しましょう。

答えは2です。
R.5.1 無線工学B(2回目) A-3
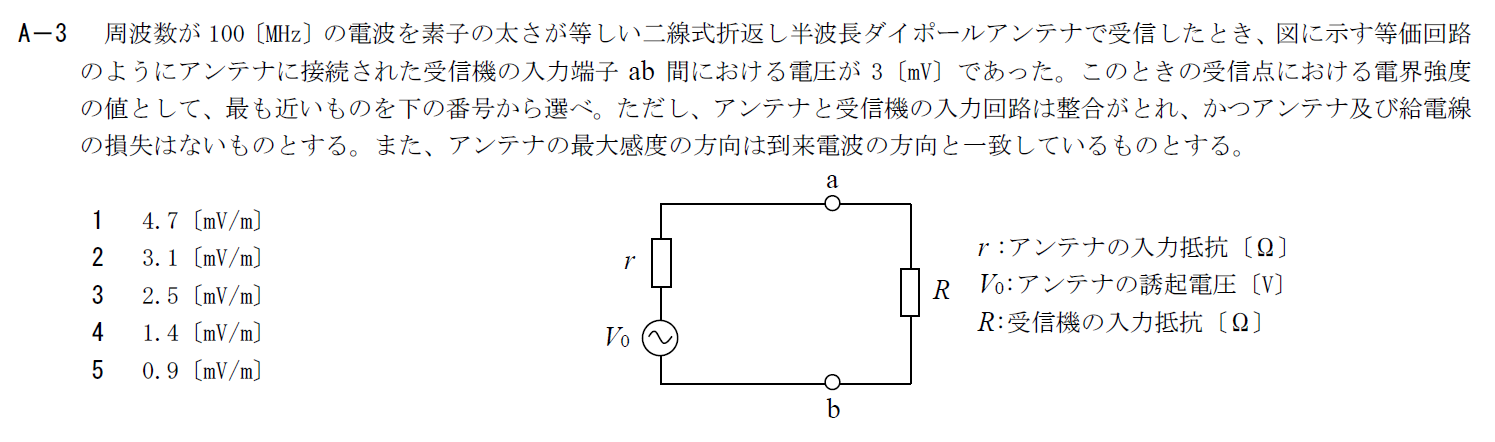
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学B A-3
受信機入力端子の電圧から二線式折り返し半波長ダイポールアンテナが受信する電界強度を計算する問題です。
この問題は令和3年7月1回目A-4で出題されています。 計算に使うパラメータが異なっていることに注意して計算しましょう。
周波数が100MHzなので、波長が1[m]となります。
計算方法は下記の記事をご参照ください。

この記事の計算式に代入すると \[ E=3.14\rm{[mV/m]} \] となります。
以上から答えは2です。
R.5.1 無線工学B(2回目) A-4

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学B A-4
アンテナ利得について誤った選択肢を選ぶ問題です。
誤った選択肢は3です。
反射損$M$は \[ M=\frac{1}{1-|\Gamma |^2} \] となります。
$1-|\Gamma |^2$は不整合があるときの進行波成分の割合を表します。 反射損を考える場合はこれの逆数にする必要があります。
以上から答えは3です。
R.5.1 無線工学B(2回目) A-5

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学B A-5
絶対利得$G$のアンテナの実効面積を求める問題です。
この問題では微小ダイポールアンテナの実効面積を出発点として、絶対利得$G$のアンテナの実効面積を求めています。
論理的にはかなり回りくどいことをしていますが、とりあえずは誘導に従って解いていきましょう。 最後にもっと簡単に実効面積を求める方法をご紹介します。
A
微小ダイポールアンテナの実効面積は \[ \frac{3\lambda^2}{8\pi} \] で表されます。
Aには「$\frac{3\lambda^2}{8\pi}$」が入ります。
微小ダイポールアンテナの受信有効電力を考えることで計算できます。 真面目に計算するとかなり大変なので、覚えておくとよいでしょう。
計算方法は余裕があれば別記事で紹介します。
B
Bでは微小ダイポールアンテナの絶対利得を聞かれています。 微小ダイポールアンテナの絶対利得は3/2なのでBには「3/2」が入ります。
微小ダイポールアンテナでも指向性はあるので、絶対利得は必ず1より大きくなるはずです。
3/2と1/2の2択なら3/2と答えるのは容易でしょう。
C
まず、等方性アンテナの実効面積$S_i$を求め、それを(2)で与えられた式に代入することで、計算したい実効面積$S$を計算します。
ここまでの空欄で、微小ダイポールアンテナの実効面積と絶対利得が分かっているので、(2)の式に代入して$S_i$を求めましょう。 \[ S_i=S_s/G_s=\frac{\lambda^2}{4\pi} \] です。
この結果を(2)の式に代入して、$S$について解くと \[ S=GS_i=G\frac{\lambda^2}{4\pi} \] となります。
そのため、Cには「$G\frac{\lambda^2}{4\pi}$」が入ります。
以上から答えは3です。
まとめ
今回は令和5年1月の無線工学B(2回目)の試験A-1~A-5の問題について解説しました。 覚えるのが面倒くさい電界強度や実効面積を使う問題が多く出題されています。 一度自分で求めておくと試験の時ぱっと思い出せることもあるので、公式としてではなくそれを計算する論理を理解しておきましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント