令和3年7月の1陸技の試験2回目の無線工学AのA-6～10の問題について解説します。
R.3.7 無線工学A（2回目） A-6
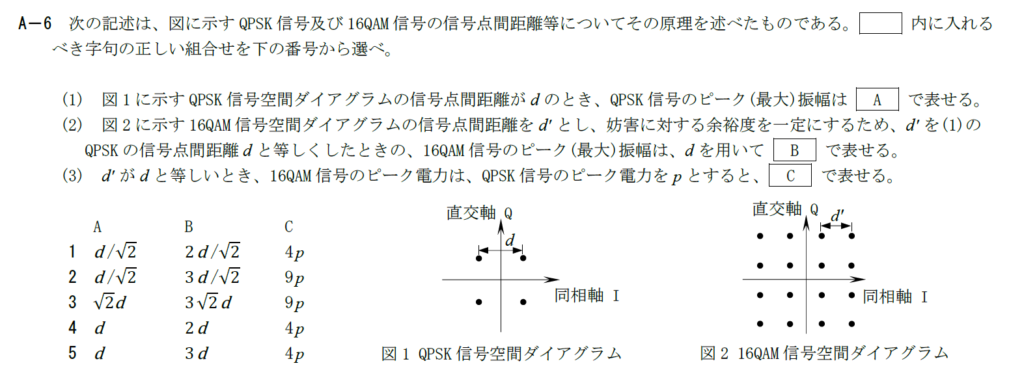
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学A A-6
QPSKと16QAMの原理に関する問題です。
A
QPSKやQAMの信号の振幅はIQ平面上で原点から信号点までの距離となります。
図1から4つの信号点はどれも原点から等距離にあります。
$(d/2,d/2)$の点を考えると、原点からの距離は$d/\sqrt{2}$です。
そのため、Aには$d/\sqrt{2}$が入ります。
B
16QAMでも考え方は同じです。
原点から最も離れている点は$(3d/2,3d/2)$,$(-3d/2,3d/2)$,$(3d/2,-3d/2)$,$(-3d/2,-3d/2)$です。
これらの点と原点との距離を求めると$3d/\sqrt{2}$となります。
そのため、Bには$3d/\sqrt{2}$が入ります。
C
AとBの比はB/A=3となります。
電力は振幅の2乗に比例するのでCには$9p$が入ります。
以上から答えは2です。
R.3.7 無線工学A（2回目） A-7
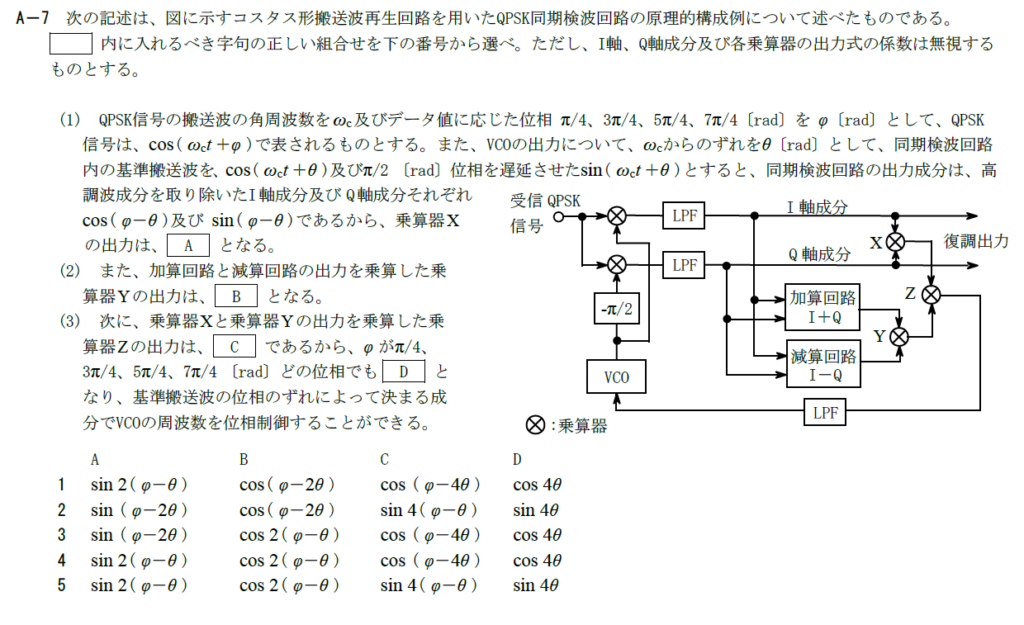
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学A A-7
QPSKの同期検波の原理に関する問題です。
A
乗算器XではI軸成分、Q軸成分の積が出力されます。
\[
\cos (\phi -\theta )\sin (\phi -\theta ) \\
=\frac{1}{2}\left\{\sin 2(\phi -\theta ) -\sin 0\right\} \\
=\frac{1}{2}\sin 2(\phi -\theta )
\]
となります。
係数を無視するので、Aには$\sin 2(\phi -\theta )$が入ります。
B
加算器出力を$\alpha$、減算器出力を$\beta$とすると
\[
\alpha=\cos (\phi -\theta ) + \sin (\phi -\theta ) \\
\beta=\cos (\phi -\theta ) – \sin (\phi -\theta )
\]
乗算器出力は
\[
\alpha \beta =\cos ^2(\phi -\theta ) – \sin ^2 (\phi -\theta ) \\
=\frac{1}{2}(1+\cos 2(\phi -\theta ))-\frac{1}{2}(1-\cos 2(\phi -\theta )) \\
=\cos 2(\phi -\theta )
\]
となります。
そのため、Bには$\cos 2(\phi -\theta )$が入ります。
C
AとBの積を考えればAと同様の計算で$\frac{1}{2}\sin 4(\phi -\theta )$となります。
そのため、Cには$\sin 4(\phi -\theta )$が入ります。
D
QPSKで使用される$\phi$では$\sin$の中の$4\theta$に$\pi$の奇数倍がたされた値になります。
$\sin (\theta +(2n+1)\pi)=-\sin \theta$なので乗算器Zの出力は常に$\sin 4\theta$です。
そのため、Dには$\sin 4\theta$が入ります。
以上から答えは5です。
R.3.7 無線工学A（2回目） A-8
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学A A-8
OFDMの受診時の同期に関する問題です。
A
OFDMの同期処理では受信した信号をFFT（高速フーリエ変換）します。
IFFTは逆フーリエ変換なのでここには当てはまりません。
そのため、AにはFFTが入ります。
B
2つの積を積分すると2つの関数に相関がないときはゼロとなります。
そのため、出力が現れるときは相関があるときです。
Bにはある（同じ波形）が入ります。
C
周波数の誤差によって位相差が生じると、同期すべき周波数と異なる信号は(2)の方法でゼロにできます。
そのため、Cには位相が入ります。
以上から答えは5です。
R.3.7 無線工学A（2回目） A-9
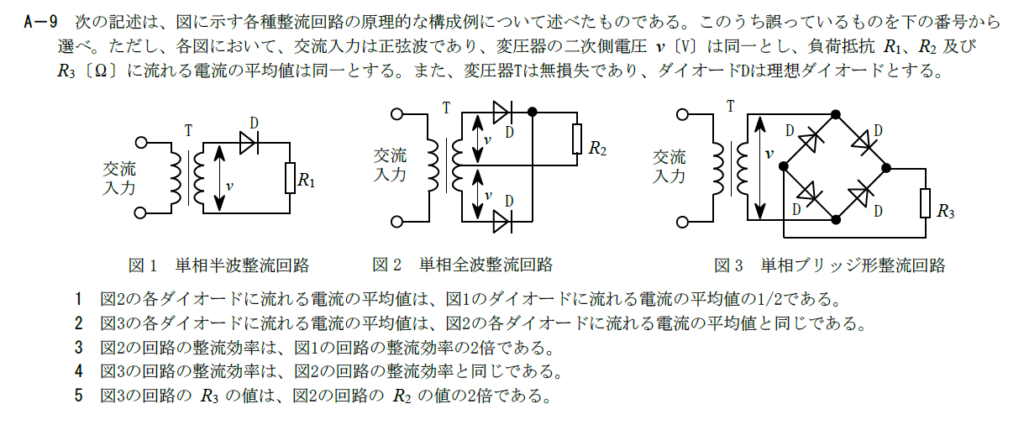
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学A A-9
整流回路に関する問題です。
誤った選択肢を選ぶ問題なのでそれぞれ見て消去法で解いてみましょう。
1
問題の条件から負荷抵抗に流れる電流の平均値は同じになります。
図1は半波整流回路、図2は全波整流回路です。
$R_2$に流れる電流の平均値が$R_1$を流れる電流の平均値と等しくなるためには、図2の各ダイオードに流れる電流は図1の1/2でなければなりません。
そのため、この選択肢は正しいです。
2
問題中のダイオードは理想ダイオードなので、順方向電流は図2と図3で同じ値になります。
そのため、この選択肢は正しいです。
3
図2は全波整流回路なので図1の半波整流回路と比べると整流効率は2倍になります。
そのため、この選択肢は正しいです。
4
2でも触れましたが、順方向電流的には図2と図3は等化なので、整流効率も同じです
そのため、この選択肢は正しいです。
5
これも2に記載したとおりで順方向電流的には等化な回路なので、$R_3$と$R_2$は同じ値でなければなりません。
そのため、この選択肢が誤りです。
以上から、答えは5です。
R.3.7 無線工学A（2回目） A-10
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学A A-10
通信衛星、特に静止衛星の食に関する問題です。
A
静止軌道は春分と秋分付近では赤道上空に位置します。
そのため、静止軌道と太陽の間に地球が入り、太陽が地球の影に隠れる時間が発生します。
Aには春分および秋分が入ります。
B
鉛蓄電池もリチウムイオン電池も二次電池なのでどちらが入っても良いと思われますが、比較的軽量なリチウムイオン電池としておくのが妥当でしょう。
確証が持てなければCを先に考えて間違った組み合わせを消すのもありです。
Bにはリチウムイオン電池が入ります。
C
地球の自転方向は北極点から見て反時計回りで、西から東に自転しています。
静止衛星は地球の自転と同じ周期で地球を公転する衛星です。
衛星からも太陽は東から上って西に落ちるように見えるはずなので、衛星がサービスエリアから東にあるほど早く食に入ることになります。
そのため、Cには早くが入ります。
以上から答えは3です。
まとめ
今回は令和3年7月1回目の1陸技の無線工学AのA-6~10を解いてみました。
過去問が多く出題される1陸技の試験ですが、ここ最近は1回の試験で2回分の過去問が出るので過去問もはかどりますね。
1陸技の申込期間もまもなく終了します。
受験する方はそろそろエンジンを掛けていきたい時期ですね。
1陸技を目指す方は頑張っていきましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人
コメント