令和4年1月の1陸技の試験1回目の無線工学BのB-1～5の問題について解説します。
R.4.1 無線工学B（1回目） B-1
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B B-1
散乱断面積に関する問題です。
(1)では散乱の概念的な説明
(2)には散乱断面積の定義
(3)でレーダー断面積（前方散乱断面積）の計算
を行っています。
ア
アでは散乱体が誘電体であった時に平面波の電磁波が入射するとどうなるか聞いています。
誘電体の場合、電磁波の電界によって分極が発生します。
そのためアには6.「分極」が入ります。
イ
散乱断面積は入射した電磁波に対する物体の実効的な断面積を表す量です。
散乱断面積は入射波に対する散乱波に比に比例するので、イには2.「$p_s/p_i$」が入ります。
ウ
散乱断面積の定義には物体の全体を囲むような球の表面積$4\pi d^2$がかかっています。
このことからも全方向に無指向性な散乱体を考えていることが推測できるでしょう。
このことからウには3.「全方向に無指向性」が入ります。
エ
入射方向と散乱方向が一致しているので物体に対して後方に進行する電波を考えていることになります。
そのため、エには4.「後方」が入ります。
オ
球の半径が波長に対して十分長い場合、入射波から見ると散乱体は半径$r$の円に見えるはずです。
そのため、オに入る金属球の散乱断面積は10.「$\pi r^2$」となります。
R.4.1 無線工学B（1回目） B-2
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B B-2
地上と衛星間の電波伝搬に関して、正誤を回答する問題です。
それぞれ見ていきましょう。
ア
この記述は正しい記述1です。
イ
この記述は正しい記述1です。
ウ
第一種減衰は電離層を通過するときの減衰ですが、周波数が低いほど減衰が大きくなります。
そのためこの記述は誤り2です。
エ
電離圏の屈折率は周波数が高いほど1に近づきます。
そのためこの記述は誤り2です。
電離層での電波の伝搬については下記の記事で解説しています。
オ
この記述は正しい記述1です。
R.4.1 無線工学B（1回目） B-3
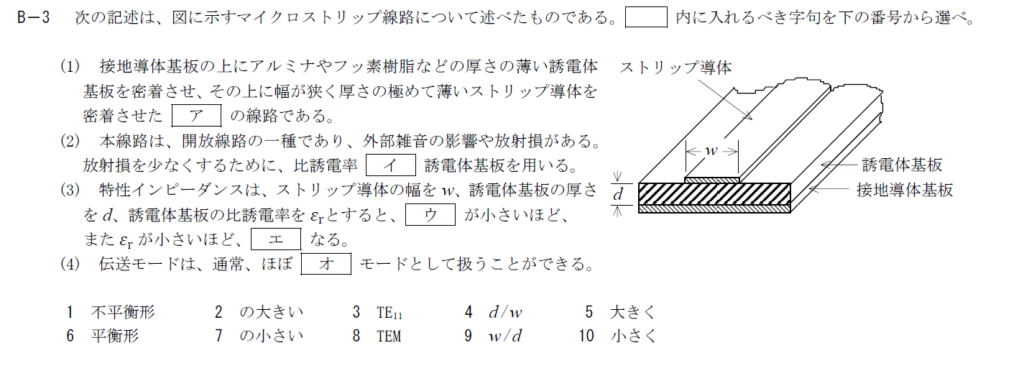
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B B-3
マイクロストリップ線路に関する問題です。
ア
マイクロストリップ線路は接地導体とストリップ導体が等価でないので不平衡形線路です。
そのため、アには1.「不平衡形」が入ります。
イ
放射損を少なくするためには比誘電率の大きい基板を使用します。
そのため、イには2.「の大きい」が入ります。
ウ、エ
(3)については特性インピーダンスについての記述ですが、内容的には$Z_0=\sqrt{\frac{L}{c}}$を考えることになります。
特に、この2つの空欄は静電容量を変えるとどうなるかということに言及しています。
マイクロストリップ線路の単位長さ辺りの静電容量は$\epsilon_r\epsilon_0\frac{w}{d}$となります。
$\epsilon_r$が小さいほど静電容量が小さくなるので、特性インピーダンスは大きくなります。
静電容量は$w/d$に比例するので、$w/d$が小さいほど特性インピーダンスは大きくなります。
以上からウには9.「$w/d$」、エには5.「大きく」が入ります。
オ
マイクロストリップ線路では電磁波TEMモードで扱うことができます。
そのため、オには8.「TEM」が入ります。
R.4.1 無線工学B（1回目） B-4
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B B-4
VSWRを測定して、アンテナの実効利得を求める問題です。
ア
信号源から見ると給電線$Z_0$とアンテナ$Z_L$が直列につながっています。
アンテナに伝送される電力は信号源から出力される電力に合成インピーダンスに対するアンテナのインピーダンスの比をかけたものに等しいです。
そのため、$P_t$は次のように書けます。
\[
P_t=\frac{V_0^2}{Z_0+Z_{max}}\frac{Z_{max}}{Z_0+Z_{max}}=\left(\frac{V_0^2}{Z_0+Z_{max}}\right)^2Z_{max}
\]
アには6.「$\left(\frac{V_0^2}{Z_0+Z_{max}}\right)^2Z_{max}$」が入ります。
イ
$Z_{max}>Z_0$として、VSWRの定義式$S=\frac{1+\left| \frac{Z_L-Z_0}{Z_L+Z_0}\right|}{1-\left| \frac{Z_L-Z_0}{Z_L+Z_0}\right|}$から$Z_L$を計算すると$Z_{max}=SZ_0$となります。
そのため、イには7.「$SZ_0$」が入ります。。
ウ
$P_t$の式にイを代入すれば8.$P_t=\frac{SV_0^2}{Z_0(1+S)^2}$となります。
エ
整合が取れいているので、②式に$S=1$を代入して9.$P_0=\frac{V_0^2}{4Z_0}$となります。
オ
式通り$P_0/P_t$を計算すると10.$P_0/P_t=\frac{(1+S)^2}{4S}$となります。
ウからオはイを間違えているとすべてが間違うので気をつけましょう。
R.4.1 無線工学B（1回目） B-5
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B B-5
角錐ホーンアンテナに関する問題です。
ア
空欄の前に「整合をとり」という言葉があるので、アには2.「反射」が入ります。
イ
ホーンアンテナでは開口面上の電磁界の位相が一様である必要があります。
そうでなければ放射位置によって電波が干渉することがあります。
そのため、イには7.「位相」が入ります。
ウ
利得の式を答える問題ですが、選択肢が3と8しかないので、問題としては開口アンテナの利得が開口面積と波長に対してどうなるかが分かっていれば、式を覚えてなくても答えられます。
開口アンテナは開口面積が大きく、波長が短いほど利得が高くなるので、ウには8.$\frac{32A}{\pi \lambda^2}$が入ります。
エ、オ
開口面積を大きくするほど利得は高くなりますが、開き書くを大きくしすぎると利得が上がりません。
そのため、エには4.「開き角」が入ります。
開き角が大きいと利得が上がらない理由は開口面の周辺部に到達する電波は中心部より長い距離を伝搬することになるため、中心部に比べて位相が遅れるからです。
前述の通り位相がそろわないと利得が下がる原因になります。
そのため、オには10.「遅れる」が入ります。
まとめ
先日行われた令和4年1月1回目の1陸技の無線工学BのB-1～5を解いてみました。
B1~5は一連の問題群を解く問題が出題されます。
たまに、一つ間違えるとそれ以降のすべてを間違えることになるような問題もありますので、気をつけて対策していきましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人
コメント