【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 無線工学A A-1~A-5）

令和4年1月の1陸技の試験、無線工学AのA-1～5の問題について解説します。

R.4.1 無線工学A（1回目） A-1
R.4.1 無線工学A（1回目） A-2
1. A
2. B
3. C
4. D
R.4.1 無線工学A（1回目） A-3
1. A,B
2. C
R.4.1 無線工学A（1回目） A-4
1. A
2. B
3. C
R.4.1 無線工学A（1回目） A-5
1. A
2. B,C
まとめ
参考文献

R.4.1 無線工学A（1回目） A-1

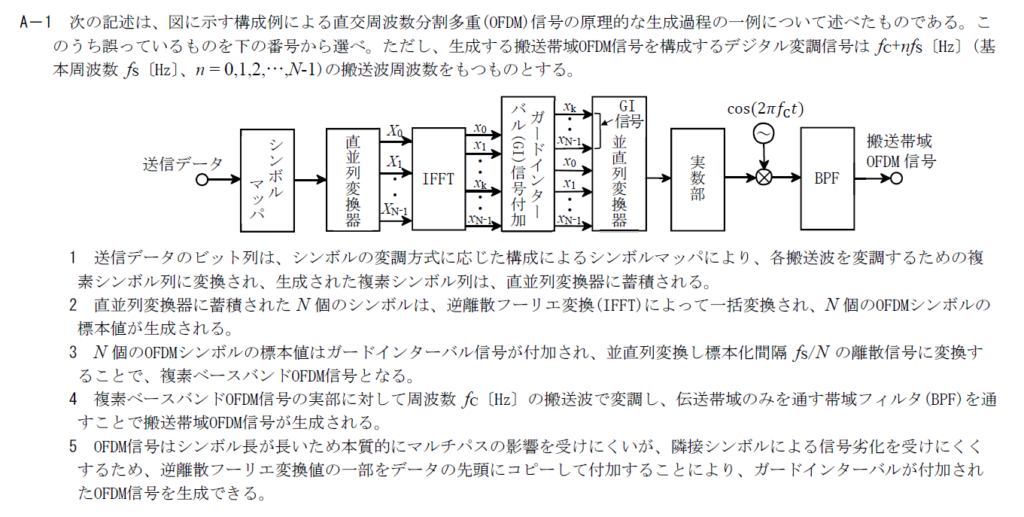
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月1回目　無線工学A A-1

直交周波数分割多重（OFDM）の信号生成原理に関して誤った選択肢を選ぶ問題です。

誤った選択肢は3です。
ガードインターバルを付加したとしても、並直列変換後の標本化間隔が変化することはありません。

そのため答えは3です。

R.4.1 無線工学A（1回目） A-2

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月1回目　無線工学A A-2

精密同一周波放送（同期放送）方式の原理に関する問題です。

A

同期放送の関係にある放送局が同一の周波数を使用していることが前提の方式なので、周波数差は小さいと考えられます。
仮に $\Delta f$ が $1[\rm{kHz}]$ もあれば中波の周波数に対しては無視できない大きさになります。
そのため、Aには「 $0.1[\rm{kHz}]$ 」が入ります。

B

2局の電界強度が等しい点で同位相であれば互いに強め合うので電界強度が2倍になります。

同位相では $\phi = 0$ または $\phi= 2\pi$ なのでBに入るのは「 $0$ および $2\pi [\rm{rad}]$ 」です。

C

逆に逆位相 $\phi =\pi$ の時は電界強度が0になります。

そのため、Cには「 $\pi [\rm{rad}]$ 」が入ります。

D

2乗検波では半導体のを通したときの歪みを使って検波するので原理的に同期放送の受信ひずみが改善されることはありません。

そのため、Dには「同期検波」が入ります。

以上から答えは5です。

R.4.1 無線工学A（1回目） A-3

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月1回目　無線工学A A-3

3次の相互変調積に関する計算問題です。
この手の面倒な計算問題はだいたい1問は出ていますね。

A,B

相互変調波の表式が与えられているので計算してみましょう。
とりあえずカッコの中を展開すると
$E_1^3\cos^3 \omega_1 t+3E_1^2E_2/l\cos^2 \omega_1t\cos \omega_2t +3E_1(E_2/l)^2\cos \omega_1t\cos^2 \omega_2t +(E_2/l)^3\cos^3 \omega_2 t$
となります。

$2\omega_1\pm \omega_2$ 、 $2\omega_2\pm \omega_1$ を含む項は第2項と第3項です。

計算としては三角関数の加法定理を使って三角関数同士の積を1つの三角関数に分解していく作業です。
係数だけなので愚直に計算しなくても当たりはつけられるでしょう。
結論から言うと $2\omega_1- \omega_2$ は $\cos^2 \omega_1t\cos \omega_2t$ を含む第2項、 $2\omega_2- \omega_1$ は $\cos \omega_1t\cos^2 \omega_2t$ を含む第3項から出てきます。
そのため、その係数を考えればAには $\frac{3}{4}KE_1^2E_2\frac{1}{l}$ 、Bには $\frac{3}{4}KE_1E_2^2\frac{1}{l^2}$ が入ります。

参考として第2項と第3項の展開結果を載せておきます。
$(第2項)=\frac{3KE_1^2E_2}{2l}\cos\omega_1 t+\frac{3KE_1^2E_2}{4l}\cos (2\omega_1 +\omega_2)t +\frac{3KE_1^2E_2}{4l}\cos (2\omega_1 -\omega_2)t \\ (第3項)=\frac{3KE_1E_2^2}{2l^2}\cos\omega_2 t+\frac{3KE_1E_2^2}{4l^2}\cos (\omega_1 +2\omega_2)t +\frac{3KE_1E_2^2}{4l^2}\cos (\omega_1 -2\omega_2)t$

C

結合量 $l$ が $l>1$ なので、 $1/l$ に比例するほうが影響が大きくなります。
そのため、Cには $2\omega_1-\omega_2$ が入ります。

以上から答えは1です。

R.4.1 無線工学A（1回目） A-4

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月1回目　無線工学A A-4

BPSK、QPSKの雑音に関する理論の問題です。

A

QPSKでは同相、直交成分でそれぞれ同じ電力になるので、それぞれの信号電力は $A^2/2$ となります。

そのため、Aには $A^2/2$ が入ります。

B

Aに記載の通り、QPSKでは信号電力搬送波電力が等しいので $SNR=CNR$ となります。

そのため、Bには $SNR=CNR$ が入ります。

C

QPSKは1シンボルあたりのビット数が2bitであり、BPSKの2倍です。

そのため、Cには3dBが入ります。

以上から答えは4です。

R.4.1 無線工学A（1回目） A-5

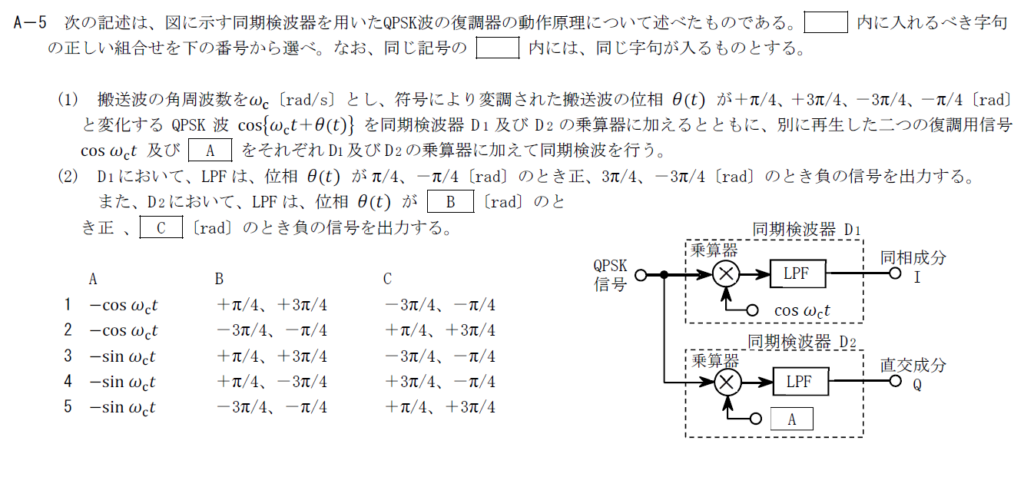
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月1回目　無線工学A A-5

同期検波を用いたQPSKの復調に関する問題です。

A

同期検波器では互いに直交するような信号をQPSK信号に乗算します。

$\cos \omega_c t$ と直交する選択肢は $-\sin \omega_c t$ です。

そのため、Aには $-\sin \omega_ct$ が入ります。

B,C

$D_2$ でのLPFに入力される信号は
$-\cos \{\omega_ct +\theta (t)\}\sin \omega_c t \\ =-\frac{1}{2}\sin \{2\omega_c t +\theta\}+\frac{1}{2}\sin \theta(t)$
となります。

LPFで第1項は落ちるので、第2項のみを考えれば問題ありません。
$\theta(t) =+\frac{\pi}{4} , +\frac{3}{4}\pi$ の時は出力が正、 $\theta(t) =-\frac{3}{4}\pi , -\frac{\pi}{4}$ の時は負の信号を出力します。

以上から答えは3です。