【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 2回目 無線工学A A-6~A-10）

令和4年1月の1陸技2回目の試験、無線工学AのA-6～10の問題について解説します。

R.4.1 無線工学A（2回目） A-6

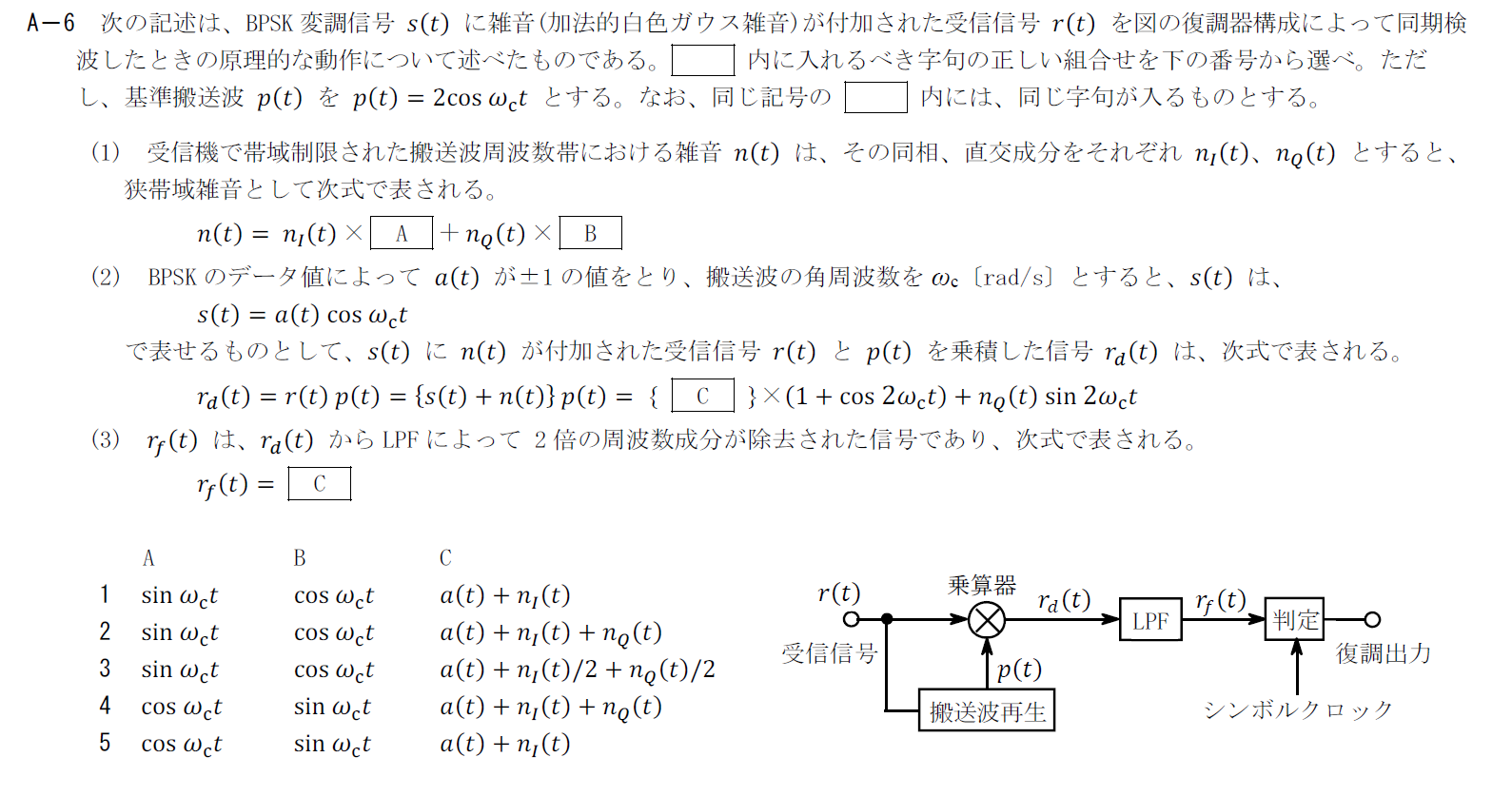
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月2回目　無線工学A A-６

BPSKの同期検波の原理に関する問題です。

A,B

AとBは雑音$n(t)$を同相、直交成分に分ける原理式の穴埋めです。

基準搬送波が$p(t)=2\cos \omega_c t$なので、同相成分には$\cos \omega_c t$が、直交成分には$\sin \omega_c t$がかかっていなければなりません。

そのため、Aには$\cos \omega_c t$、Bには$\sin \omega_c t$が入ります。

C

(2)に従って$r_d(t)$を計算してみましょう。
$$r_d(t)=\{s(t)+n(t)\}p(t)=2a(t)\cos^2 \omega_ct +2n_I(t)\cos^2 \omega_ct +2n_Q(t)\cos \sin \omega_ct \\ =\{a(t)+n_I(t)\}(1+\cos 2\omega_ct)+n_Q(t)\sin 2\omega_c t$$
最後の変形では三角関数の倍角の公式を使いました。

この結果からCには$a(t)+n_I(t)$が入ります。

以上から答えは5です。

R.4.1 無線工学A（2回目） A-7

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月2回目　無線工学A A-7

FMのS/N改善係数の計算に関する問題です。
計算式は問題文に記載されているのでそれを使いましょう。

$I$（真数）の式中で$m_f$だけ与えられていません。

まず、$m_f$を計算しましょう。

$f_d=f_pm_f$が成り立つので、$m_f=f_d/f_p=2$となります。

与えられた式にそれぞれのパラメータを代入すれば
$$I=\frac{3m_f^2B}{2f_p} \\ =\frac{3 \times 2^2 \times 20 \times 10^3}{2 \times 3 \times 10^3} \\ =40$$
となります。

dB表記に直すと
$$I[\rm{dB}]=10\log 40 =16$$
となります。

以上から答えは3の16[dB]です。

R.4.1 無線工学A（2回目） A-8

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月2回目　無線工学A A-8

スーパヘテロダイン受信機で発生する影像周波数に関する問題です。

A

影像周波数は希望波以外に検波される周波数です。

文中にあるように$f_u$が検波される可能性があるので$f_u$が影像周波数です。

そのため、Aには$f_u$が入ります。

B,C

中間周波数を低くすると希望波の周波数以上中間周波数を希望波から離すことができないませんが、中間周波数を高くすることで影像周波数と希望波との間隔を広げやすくなります。

そのため、Bには「高く」が入ります。

また、高周波増幅回路の周波数選択度をよくすることで妨害波を増幅させないようにして影像周波数の影響を小さくできます。

Cには「高周波増幅回路」が入ります。

以上から答えは4です。

R.4.1 無線工学A（2回目） A-9

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月2回目　無線工学A A-9

無停電電源装置(UPS)に関する問題です。

一般的なUPSは交流電力を出力します。

入力は商用電源の交流電力や蓄電池からの直流電力です。

4の記述では直流電力を負荷に供給すると記載されているのでこれが誤りです。

以上から答えは4です。

R.4.1 無線工学A（2回目） A-10

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年1月2回目　無線工学A A-10

整流回路出力の各パラメータに関する計算問題です

順番に計算していきましょう。

リプル率$\gamma$は
$$\gamma =\frac{\rm{交流分の実効電圧}}{\rm{定格電圧}}=\frac{0.36}{6}=0.06$$
となります。
そのため$\gamma$は6.0%です。

交流分の電圧変動は$2\sqrt{2}\times 0.36$です。
$\delta$を計算すると
$$\delta =\frac{2\sqrt{2}\times 0.36}{6}=0.170$$
となります。
近い値は16.7%です。

$\eta$は入力電力と出力電力の比なので
$$\eta =\frac{10}{13}=0.769$$
です。
そのため近い値は77%です。

以上から答えは5です。

まとめ

今回は令和4年1月2回目の1陸技の無線工学AのA-6~10を解いてみました。
無線工学Aでは三角関数の計算が多く出題されます。
すべてを覚えておく必要はありませんが、加法定理などから導けるようにしておきましょう。
次の7月の試験申込み期間に入りましたね。
そろそろ試験勉強も本格的になってきた頃でしょう。
本サイトも活用して合格を勝ち取ってください。

勉強法

第一級陸上無線技術士の勉強法とおすすめ参考書

参考文献

電磁気学をちゃんと学びたい人向け

上の難易度が高い人