令和4年7月の1陸技の試験、無線工学AのB-1～5の問題について解説します。
R.4.7 無線工学A（1回目） B-1
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月1回目 無線工学A B-1
BPSK復調器の基準搬送波再生回路に関する問題です。
ア
(2)では入力電圧$e_i$を2逓倍するので
\[
e_O=\cos^2\{2\pi f_ct+\pi s(t)\} \\
=\frac{1}{2}+\frac{1}{2}\cos \{2\pi (2f_ct)+2\pi s(t)\}
\]
となります。
最後の式変形では$\cos$の倍角の公式を使いました。
この結果からアには1.「$2\pi s(t)$」が入ります。
イ
$s(t)$は”0″か”1″の値をとるので$s(t)$が変化することは$e_i$の位相が$\pi [\rm{rad}]$変化することになります。
そのため、イには「$\pi [\rm{rad}]$変化」が入ります。
ウ
搬送波の数が多いほど増幅器の非線形動作による影響が大きくなるので大きいバックオフが必要となります。
そのため、ウには4.「$2f_C$」が入ります。
エ
エの構成をPLL(Phase Locked Loop)と呼びます。
そのため、エには2.「PLL」が入ります。
オ
QPSKでは位相$\pi /4$ごとに符号を割り当てるので、4逓倍すればどの信号でも位相が$2\pi$の整数倍になります。
そのため、オには10.「4」が入ります。
R.4.7 無線工学A（1回目） B-2
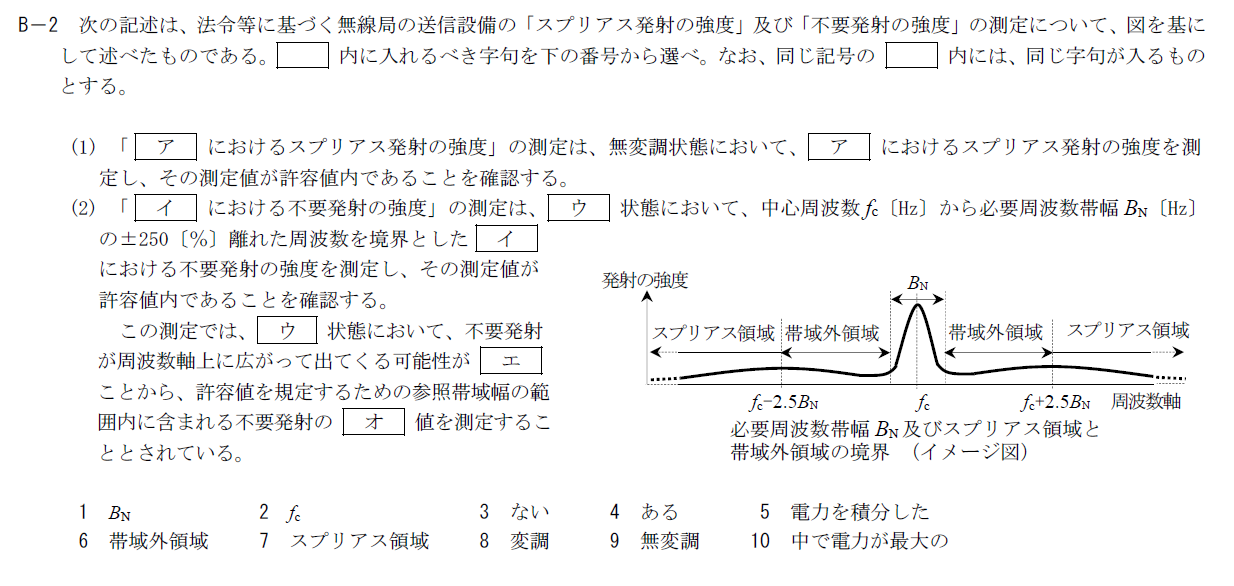
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月1回目 無線工学A B-2
「スプリアス発射の強度」と「不要発射の強度」の測定に関する問題です。
内容的には法規の問題と思ってもいいでしょう。
ア
無変調状態で測定するのは帯域外領域です。
そのため、アには6.「帯域外」が入ります。
イ
アの内容に対してイには7.「スプリアス領域」が入ります。
ウ
スプリアス領域の測定では変調状態の電波を使用します。
そのため、ウには8.「変調」が入ります。
エ
変調波は周波数軸上で広がりを持っているので、不要発射も周波数軸上で広がって出てくる可能性があります。
そのため、エには4.「ある」が入ります。
オ
エの通り、周波数軸上で広がりを持つので、電力の最大値では評価できません。
範囲内の電力を積分して測定する必要があります。
そのため、オには5.「電力を積分した」が入ります。
R.4.7 無線工学A（1回目） B-3
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月1回目 無線工学A B-3
送受信機で発生するひずみに関する正誤問題です。
ア
アの記述は正しい記述です。
そのため、アの答えは1です。
イ
この記述は誤りです。
A級増幅器は特性が直線な部分を使うので、非線形ひずみは発生しません。
そのため、イの答えは2です。
ウ
この記述も誤りです。
前半の記述は正しいですが、後半の記述が誤りです。
群遅延ひずみも周波数特性は平坦ではありません。
そのため、ウの答えは2です。
エ
この記述も誤りです。
この説明は非直線ひずみの説明となっています。
そのため、エの答えは2です。
オ
この記述も誤りです。
非直線ひずみを小さくする方法としては正帰還ではなく負帰還が使用されます。
そのため、オの答えは2です。
R.4.7 無線工学A（1回目） B-4
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月1回目 無線工学A B-4
マイクロ波用サーミスタ電力計の動作原理に関する問題です。
ア
サーミスタ電力計はマイクロ波を熱に変換してその温度変化を測定する電力計です。
入りうる選択肢は10[W]と10[mW]のいずれかですが、10[W]も発熱には耐えられない可能性が高いです。
そのため、アは6.「10[mW]」です。
イ
$R_1$で消費される電力$P_1$は$P_1=I_1^2R_1$で表されます。
ブリッジ回路が平行な時$\frac{R_1}{R_2}=\frac{R_3}{R_4}$なので、上記の式に$R_1$を代入すると
\[
P_1=I_1^2R_2R_3/R_4
\]
となります。
そのため、イは7.「$I_1^2R_2R_3/R_4$」です。
ウ
ここはイと同じように考えればいいので、ウは3.「$I_2^2R_2R_3/R_4$」です。
エ
イとウの結果を③の式に代入すると
\[
P_m=P_1-P_2=(I_1^2-I_2^2)R_2R_3/R_4
\]
となります。
そのため、エは4.「$(I_1^2-I_2^2)R_2R_3/R_4$」です。
オ
線路と同様に不整合があると反射が起きます。
そのため、オは5.「反射」です。
R.4.7 無線工学A（1回目） B-5
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月1回目 無線工学A B-5
QPSKやOQPSKに関する問題です。
ア
OQPSKは時間的にオフセットをかけることによってIQ平面上の原点を通らなくしています。
これにより振幅変動を小さくできます。
そのため、アは1.「小さく」が入ります。
イ
IチャネルとQチャネルの極性が同時に変化するとIQ平面上で原点をはさんで反対側に移動するので位相でいうと$\pi$変化することになります。
そのため、イは9.「$\pi$」です。
ウ
原点はIQチャネルの振幅が両方ゼロとなることを意味するので、包絡線の振幅は0になります。
そのため、ウは3.「0」です。
エ
包絡線が原点を通るとき振幅0を通るので振幅変動が最大になります。
1シンボル長の半分（1/2周期）IQチャネルを時間的にオフセットすることで原点を通らなくできます。
1シンボル長オフセットすると原点を回避することはできません。
そのため、エは7.「1シンボル長の半分」です。
オ
エの時、シンボルはIまたはQ軸に対して対称な位置に移動するので位相変化としては$\pi/2$となります。
そのため、オは5.「$\pm \pi/2\rm{[rad]}$」です。
まとめ
今回は令和4年7月無線工学Aの1回目のB-1~B-5について解説しました。
無線工学AではB問題は配点は低いですが、1つ間違えるとすべて間違ってしまう問題もあるので気を付けて解きましょう。
落ち着いて考えれば解ける問題も多いです。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人
コメント