【過去問解説】令和4年7月の1陸技試験問題を解いてみた（R4.7 2回目無線工学B A-1~A-5）

令和4年7月の1陸技の試験2回目の無線工学BのA-1～5の問題について解説します。

R.4.7 無線工学B（2回目） A-1
1. A
2. B
R.4.7 無線工学B（2回目） A-2
R.4.7 無線工学B（2回目） A-3
R.4.7 無線工学B（2回目） A-4
R.4.7 無線工学B（2回目） A-5
まとめ
参考文献

R.4.7 無線工学B（2回目） A-1

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年7月2回目　無線工学B A-1

微小ダイポールアンテナから発生する電界に関する問題です。この問題については計算の仕方は令和3年7月1回目A-5と同じで、違いはダイポールからの距離だけです。今回は$r=5\lambda$と波長に対して長い領域について聞かれています。

A

Aについては令和3年7月1回目A-5と全く同じで、$|E_1|=|E_2|=|E_3|$となるような$r$を求めます。その結果、Aは$r=\lambda/(2\pi)$となります。下記も参考にしてください。

【過去問解説】令和3年7月の1陸技試験問題を解いてみた（R3.7 1回目　無線工学B A-1~A-5）

１陸技令和3年7月の無線工学Bの問題を解いてみました。今回は第1回A-1~5を解きました。

B

Bについては令和3年7月1回目A-5と違って、距離が十分離れたところでの電界を計算することになっています。 $|E_1|, |E_2|, |E_3|$はこの順番に$r$が大きくなるほど小さくなっていきます。そのため、一番大きくなる$|E_1|$を基準に考えていきましょう。 $r=5\lambda$を代入すると \[ |E_1|:|E_2|:|E_3|=\frac{1}{5\lambda}:\frac{\lambda}{2\pi (5\lambda)^2}:\frac{\lambda^2}{4\pi^2 (5\lambda)^3} \\ =1:0.032:0.001 \] となります。そのため、Bには「$1:0.032:0.001$」が入ります。以上から、答えは5です。

R.4.7 無線工学B（2回目） A-2

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年7月2回目　無線工学B A-2

アンテナの比帯域幅に関して誤った選択肢を選ぶ問題です。誤った選択肢は3です。半波長ダイポールアンテナでは素子が太いほど帯域幅が広くなります。そのため、答えは3です。

R.4.7 無線工学B（2回目） A-3

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年7月2回目　無線工学B A-3

アンテナの実効面積に関する計算問題です。利得$G_1$実効面積$A_1$のアンテナと利得$G_2$実効面積$A_2$のアンテナがある時、利得は実効面積に比例するので、次の式が成り立ちます。 \[ \frac{G_1}{G_2}=\frac{A_1}{A_2} \] また、半波長ダイポールアンテナの実効面積は$0.13\lambda^2$です。考えるアンテナの半波長ダイポールアンテナに対する相対利得が$20\rm{dB}$なので、$10\log \frac{G_1}{G_2}=20$です。最初の式の両辺をdBに直して相対利得を代入すると \[ 10\log \frac{A}{0.13\lambda^2}=20 \] となります。この式を$A$について解くと \[ A=13\lambda^2=13\left(\frac{300}{500}\right)^2=4.68 \simeq 4.7[\rm{m^2}] \] 以上から答えは4です。

R.4.7 無線工学B（2回目） A-4

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年7月2回目　無線工学B A-4

電波の伝搬に関する計算問題です。計算するのは伝搬損失と絶対利得です。利得はフリスの公式から伝搬損失を使って、伝搬距離を$d$とすると伝搬損失は$\frac{4\pi d^2}{\lambda^2}$で表せます。これをdBに直すと \[ L=10\log \left( \frac{4\pi d}{\lambda} \right)^2 \\ =20\log (4 \pi \times 20 \times 20 \times 10^3) \\ =20(4\log 2 +\log \pi +5)=134 \] となります。フリスの公式から送信電力を$P_t$、送信利得を$G_t$、受信入力レベルを$P_r$とすると \[ P_r=\frac{G_rG_tP_t}{L} \] となります。ここから$G_r$を計算すると \[ G_r=\frac{P_rL}{G_tP_t} \] となります。これをdBに直して計算すると \[ G_r=-40+134-30-40=24\rm{[dB]} \] となります。以上から答えは3です。

R.4.7 無線工学B（2回目） A-5

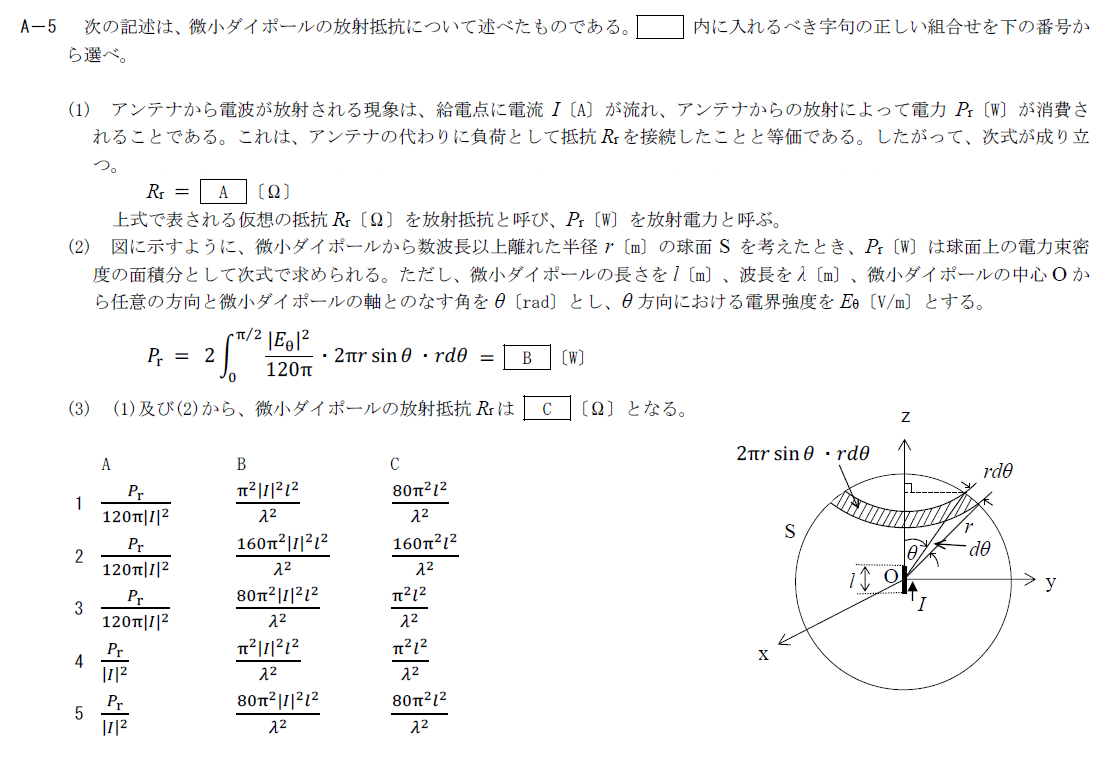
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年7月2回目　無線工学B A-5

微小ダイポールの放射抵抗の計算問題です。この問題は令和3年1月1回目のA-5の問題と全く同じです。

【無線】1月の1陸技試験問題を解いてみた（R3.1 1回目　無線工学B A-1~A-5）

1月の1陸技の無線工学Bの試験問題と解いてみました。

以上から答えは2です。

まとめ

今回は令和4年7月の無線工学B(2回目)の試験A1~A-5の問題について解説しました。 1陸技は過去問と全く同じ問題や数字を変えただけの問題も多く出題されます。数字が違うと答えが全く違うこともありますので、答えではなく問題の解き方をしっかり身につけましょう。勉強法第一級陸上無線技術士の勉強法とおすすめ参考書