令和3年7月の1陸技の試験、無線工学AのB-1～5の問題について解説します。 1陸技の各科目の最後の5問は文中の空欄を語群から選んで解答する問題が多いです。 特にこの手の問題は上下に並んだ選択肢が対になっていることが多く、それぞれの空欄は実質的な2択問題となっていることがほとんどです。
R.3.7 無線工学A（1回目） B-1
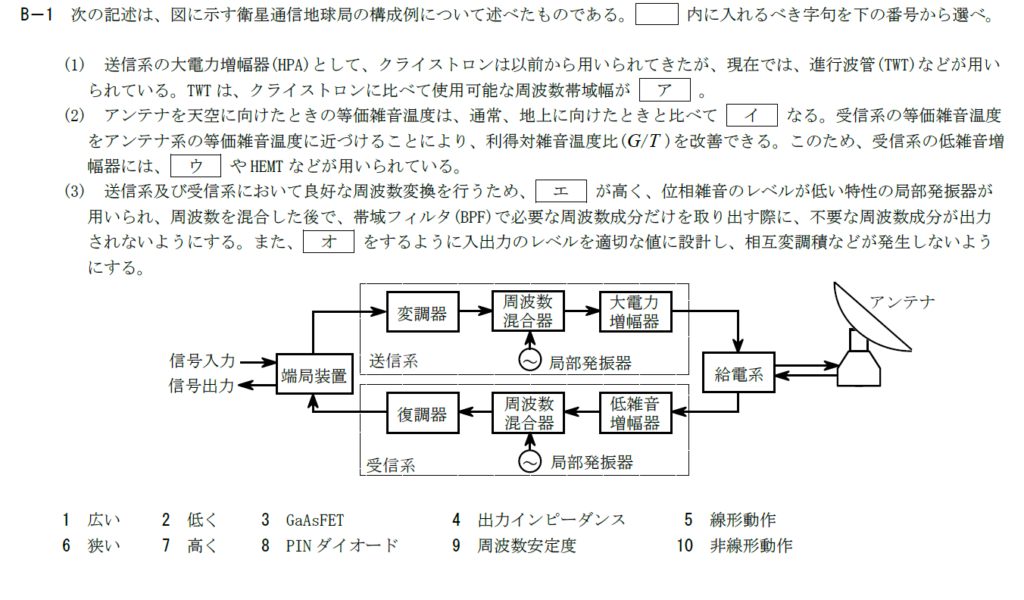
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学A B-1
衛星通信地球局の構成に関する問題です。
ア
クライストロンも進行波管も電子管の一種ですが、一般に進行波管の方がクライストロンより帯域が広くなります。
そのため、アには1.広いが入ります。
イ
アンテナを天空に向けたときは太陽や宇宙からのノイズを受信しますが、地上の方がはるかに近くに多くのノイズ源があるため、通常地上にアンテナを向けたときのほうがノイズが大きくなります。
そのため、イには2.低くが入ります。
ウ
ウには3.GaAsFETが入ります。
覚えていなくても語群の中にこれ以外に増幅器として使えるものがありません。 PINダイオードは主にスイッチングやアッテネータの用途で使われます。
エ
良好な周波数変換を行うには安定した局部発振器が必要です。
そのため、エには9.周波数安定度が入ります。
出力インピーダンスを高くしても周波数変換にはあまり旨味がありません。
オ
相互変調積などのひずみは素子の非線形動作によって生じます。
そのため、不要な周波数成分を出力したくなければ線形動作するように入出力レベルを設計します。
オに入るのは5.線形動作です。
R.3.7 無線工学A（1回目） B-2
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学A B-2
FFTアナライザに関する問題です。
FFTアナライザは入力信号をA/D変換した後、フーリエ変換という演算によって周波数領域のデータを得る測定器です。
ア
アナログのスペクトラムアナライザは周波数掃引によって周波数軸のデータを得るので、位相の情報は入りません。
一方、FFTアナライザではフーリエ変換によってデータを得るので、周波数成分ごとの振幅の他に位相の情報も得ることができます。
そのため、アには6.振幅及び位相が入ります。
イ
周波数分解能を上げるほど演算に時間がかかるので、時間分解の方は下げる必要があります。
そのため、イには2.下げるが入ります。
ウ
FFTアナライザでは時系列の入力信号を演算するので限られた時間の信号を解析することができます。 アナログのスペクトラムアナライザでは掃引時間の関係で解析できない場合があります。
そのため、ウには8.できるが入ります。
エ
FFTアナライザでは演算するための入力信号を有限に区切るために窓関数を使います。 リーケージ誤差を減少させるためには適切な窓関数を使用する必要があります。
IFFTは逆フーリエ変換のことなので、リーケージ誤差とは関係ありません。
そのため、エには4.窓関数が入ります。
オ
サンプリング周波数の半分の周波数をナイキスト周波数と言います。 ナイキスト周波数はその標本化周波数で正しく信号を再現できる最大の周波数です。
分解能帯域幅はアナログのスペクトラムアナライザのいわゆるRBWのことでFFTの標本化の話とは無関係です。
そのため、オには10.ナイキスト周波数が入ります。
R.3.7 無線工学A（1回目） B-3
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学A B-3
誤り訂正符号に関する問題です。 この問題は珍しく語群の上下段が対になっていません。
ア
アに入るのは誤り訂正符号化する装置なので1.符号器が入ります。
イ
イには受信側の符号化された信号をもとに戻す装置が入るので、イに入るのは6.復号器です。
ウ
符号化率は符号語全体の中のチェックビットの割合なので、ウには3.k/nが入ります。
エ
ブロック符号ではブロックごとにチェックビットを付与するので、あるブロックのチェックビットは同じブロックの情報ビットだけの関数となります。
そのため、エには8.同じブロックの情報ビットだけのが入ります。
オ
畳み込み符号では過去にわたる複数の情報ビットから符号化します。
そのため、オには4.過去にわたる複数の情報ビットのが入ります。
この積分結果は入力電圧と基準電圧を入力した時、両方符号が逆で出力されるので打ち消すことができます。
R.3.7 無線工学A（1回目） B-4
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学A B-4
相互変調に関する問題です。 暗記していればすぐ解ける類の問題ですが、ここでは少し丁寧に導出してみます。
ア
まず、入力を正弦波で$e_i=A_1\sin(\omega_1 t)+A_2\sin(\omega_2 t)$とします。 $\omega_1=2\pi f_1, \omega_2=2\pi f_2$です。 ここでは位相は無視します。
3乗の項は次のようにかけます。 \[ e_i^3=A_1^3\sin^3(\omega_1 t)+3A_1^2A_2\sin^2(\omega_1 t)\sin(\omega_2 t)+3A_1A_2^2\sin(\omega_1 t)\sin^2(\omega_2 t)+A_2^3\sin^3(\omega_2 t) \] アで話題になっているのは第2項と第3項です。
第2項について考えてみましょう。 \[ (第2項)=3A_1^2A_2\frac{1}{2}(1-\cos(2\omega_1t))\sin\omega_2t \\ =\frac{3}{2}A_1^2A_2\sin\omega_2 t-\frac{3}{4}A_1^2A_2(\cos(2\omega_1+\omega_2)t+\sin(2\omega_1-\omega_2)t) \]
最後の2項から$2f_1\pm f_2$が現れることがわかります。 第3項も同様に計算できるので$2f_2\pm f_1$が現れます。
そのため、アには5.2が入ります。
イ
希望周波数や中間周波数はフィルタを通ってしまうのでこれらの周波数と3乗成分が等しくなると妨害が起きます。
そのため、イには2.中間周波数が入ります
ウ
周波数差を$\delta f$とすると$F_2=F_1+\Delta f, F_3=F_1+2\Delta f$となります。 アで計算した結果を$F_1, F_2, F_3$について考える必要がありますが、ここでは関係ある周波数について計算します。
まず、$F_1$を希望周波数とすると$2F_2-F_3=F_1$となるため、$F_1$は希望周波数に妨害を受けます。
次に、$F_3$を希望周波数とした場合を考えましょう。 このときも$2F_2-F_1=2F_1+2\Delta f-F_1=F_1+2\Delta f=F_3$となるため、$F_3$でも希望周波数に妨害を受けます。
以上から、ウには3.$F_2$が入ります。
エ
非直線動作になるのは利得が大きいときです。
そのため、エには9.小さくが入ります。
オ
$L=10\log l$とすると、アの計算から3次の相互変調積は振幅の3乗に比例しているので減衰器を入れると$l^3$で減衰します。 デシベルに直せば$3L$[dB]減衰することになります。
以上から6.3Lが入ります。
R.3.7 無線工学A（1回目） B-5
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学A B-5
FM通信のエンファシスに関する問題です。
ア
図の積分回路で$e_2/e_1$はRとCの合成抵抗とCのリアクタンスの比と等しくなります。 $e_2/e_1=\frac{1/(j\omega C)}{R+1/(j\omega C)}=\frac{1}{1+j\omega CR}$で減衰します。
以上からアには7.$1/(1+j\omega \tau)$となります。
イ
$e_{20}$の定義から$e_{20}=|e_1|$となります。 そのため、周波数特性は次のようになります。 \[ |e_2/e_{20}|=\left|\frac{1}{1+j\omega \tau}\frac{e_1}{|e_1|}\right| \\ =\left|\frac{1}{1+j\omega \tau}\right| \\ =\frac{1}{\sqrt{1+\omega^2\tau^2}} \]
そのため、イには8.$1/\sqrt{1+\omega^2\tau^2}$が入ります。
ウ
プレエンファシス回路はディエンファシス回路の逆の動作をする必要があるので、プレエンファシス回路は微分回路となります。
そのため、ウには1.微分が入ります。
エ
プレエンファシス回路の周波数特性は特性はディエンファシス回路と合わせて平坦(1)となる必要があるので、イの逆数である$\sqrt{1+\omega^2\tau^2}$が入ります。
そのため、エには10.$\sqrt{1+\omega^2\tau^2}$が入ります。
オ
ここは覚えている必要があります。 我が国のFM放送では50[$\mu$s]が使用されます。
そのため、オには4.50が入ります。
まとめ
今回は先日行われた令和3年7月1回目の1陸技の無線工学AのB-1~5を解いてみました。
今年の7月の1回目の試験は無線工学A,Bを一通り解けました。 次回は2回目の無線工学Bを解こうと思います。
過去問が多く出題される1陸技の試験ですが、ここ最近は1回の試験で2回分の過去問が出るので過去問もはかどりますね。 次の試験を目指すならこの時期からであれば次の試験まで十分に時間が取れます。 1陸技を目指す方は頑張っていきましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人
コメント