令和4年1月の1陸技の試験2回目の無線工学BのA-16~20の問題について解説します。
R.4.1 無線工学B(2回目) A-16

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B A-16
対流圏伝搬におけるフェージングの主に用語の意味を問う問題です。
A
(1)はシンチレーションフェージングに関する説明です。
シンチレーションフェージングは大気の屈折率の不規則な変動によって生じるフェージングです。 シンチレーションとはもともと大気のゆらきによって構成が瞬く現象のことを指します。
太陽フレアもシンチレーションを引き起こす要因の一つですが、シンチレーションフェージングの直接な原因は大気の屈折率の変化なので、「大気の屈折率」を選ぶのが適切でしょう。
そのため、Aには「大気の屈折率」が入ります。
B
(2)は干渉性k形フェージングに関する説明です。
こちらも大気の変動によって発生するフェージングで、直接波と大地反射波が受信するときにその途中で大気が変動して、干渉状態が変化することにより発生します。
ここでいうkは地球の等価半径係数です。 大気が変化すると等価半径係数が変化するため、直接波と大地反射波の経路差が変化するのでフェージングの原因となります。
そのため、Bには「大地反射波」が入ります。
C
(3)は回折性k形フェージングに関する説明です。
回折性k形フェージングは等価半径係数の変化によって回折損が変化することで発生します。 回折損はkが小さくなるほど大きくなります。
これはkが小さいほど地球の等価半径が小さくなるので、地球の形による回折が大きくなるためです。
そのため、Cには「小さく」が入ります。 以上から答えは3です。
R.4.1 無線工学B(2回目) A-17

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B A-17
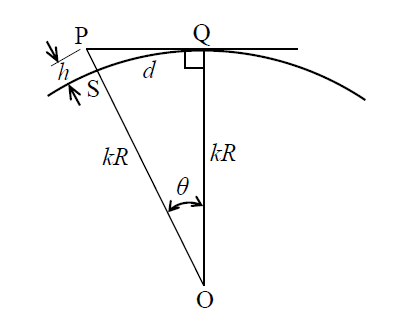
模式図
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年1月1回目 無線工学B A-14
球面大地での電波の伝搬に関する計算問題です。
この問題は令和3年1月の1回目A-14と類似問題です。
図のような位置関係を考えます。
送信点をS、アンテナ位置をP、地球中心をO、Pから引いた等価地球への接線と等価地球の接点をQとします。 まず、三角形OPQを考えます。
このとき \[ \cos \theta =\frac{KR}{KR+h}=\frac{KR(KR-h)}{(KR+h)(KR-h)}=\frac{(KR)^2\left(1-\frac{h}{KR}\right)}{(KR^2)\left\{1-\left(\frac{h}{KR}\right)^2\right\}} \\ \simeq 1-\frac{h}{KR} \] 最後の近似は$KR>>h$なので$1>>\left(\frac{h}{KR}\right)^2$として無視しました。 次に、$\theta$を考えます。 弧SQを考えると$\theta =\frac{d}{KR}$となります。 与えられた式から \[ \cos \theta =1-\frac{\theta ^2}{2}=1-\frac{d^2}{2K^2R^2} \] となります。 ここまでの2式から \[ 1-\frac{h}{KR}=1-\frac{d^2}{2K^2R^2} \\ h=\frac{d^2}{2KR} \] となります。 $d=26, K=\frac{4}{3},R=6370$を代入すると答えが求まります。
計算すると$h=40\rm{[m]}$です。
以上から答えは3です。
R.4.1 無線工学B(2回目) A-18

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B A-18
この問題は明らかに間違った選択肢が1つあります。
それは2です。
円偏波のアンテナであれば、そこから放射される電波に直線偏波の成分が含まれているので直線偏波のアンテナも使用できます。
そのため、答えは2です。
R.4.1 無線工学B(2回目) A-19

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B A-19
雑音指数から最小受信電界強度を求める問題です。
A
(1)では受信機入力端の雑音とアンテナからの有能信号電力を計算しています。
問題の図の通り、アンテナの出力端に誘起される電圧は$E_{\rm{min}}l_e$です。
アンテナから見ると放射インピーダンスと受信機の入力インピーダンスが直列に接続されています。 これらは整合しているので、受信機の入力端に掛かる電圧は$E_{\rm{min}}l_e/2$です。
そのため、アンテナから受信機に入力される有能信号電力$S_i$は
\[ S_i=\frac{(E_{\rm{min}}l_e)^2}{4R_r} \]
となり、Aにはこの値が入ります。
B
$S/N$は次のように表せます。
\[ S/N=\frac{S_i}{FkTB} \]
ここから$S_i$について解けば \[ S_i=FkTB(S/N) \] となります。
Bにはこの値が入ります。
C
②の式を③式に代入して$E_{\rm{min}}$について解きます。
\[ \frac{(E_{\rm{min}}l_e)^2}{4R_r}=FkTB(S/N) \\ E_{\rm{min}}=\frac{1}{l_e}\sqrt{4FkTBR_r(S/N)} \] Cにはこの値が入ります。
以上から、答えは5です。
R.4.1 無線工学B(2回目) A-20

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学B A-20
開口面アンテナの放射電磁界の領域に関する用語の問題です。
A
(1)はアンテナのごく近傍で、静電界や誘導電磁界が優勢な領域と記載されているので、リアクティブ近傍界の説明となっています。
フレネル領域はこの領域から更に外側で放射電磁界が優勢な領域です。
そのため、Aには「リアクティブ近傍界」が入ります。
B
(2)は放射電磁界成分が優勢な領域についての説明です。
文中では放射エネルギーの角度分布がアンテナからの距離によって変化する領域とあるので、放射近傍界領域(フレネル領域)の説明となっています。
フレネル領域では開口面の各点から放射された電波同士が干渉するので距離に対して振動するように放射エネルギーが分布します。
遠方界領域(フラウンホーファー領域)では放射エネルギーの分布が距離によってほとんど変化しません。
そのため、Bには「近傍界」が入ります。
C
アンテナの放射特性はアンテナから十分離れた領域、つまり放射遠方界によって定義されますが、電波暗室等で測定する場合、十分な距離が取れることは少ないです。
そこで、近傍界の測定で得られた結果から計算で放射特性を求めます。
そのため、Cには「放射遠方界」が入ります。
以上から、答えは5です。
まとめ
令和4年1月2回目の1陸技の無線工学BのA-16~20を解いてみました。 1陸技では計算問題も多く出題されます。計算が面倒な問題も多いですが、うまく工夫して簡単に素早く計算する練習をしておきましょう。 1陸技は過去問と同じまたは類似問題が出題されやすい試験なので、合格に向けた過去問演習は非常に重要となります。 このサイトのコンテンツも充実させていきたいと思いますので参考にしていただければ幸いです。 勉強法
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント