R.3.12 無線工学 B-1

出典:公益財団法人 日本無線協会 第一級アマチュア無線技士 R3年12月 無線工学B-1
ア
選択肢的に磁束密度だけ公式からの推測が難しく覚えている必要があります。 磁束密度の単位はテスラ[T]です。磁束の単位はウェーバ[Wb]で磁束密度は単位面積あたりの磁束なので[$\rm{Wb/m^2}$]と表すこともあります。 そのため、アの答えは8.テスラ[T]です。イ
電束密度はガウスの法則を考えるのが楽でしょう。 微分形でも積分形でもどちらでもいいです。 ここではガウスの法則の積分形 \[ \int_S \vec{D}\cdot d\vec{S}=Q \] を考えてみましょう。 電束密度の単位をDとおいて両辺の単位を考えてみましょう。 左辺は電束密度を面積分しているので$\rm{D m^2}$の単位を持ちます。 一方、右辺は電荷なので$\rm{C}$の単位です。 ガウスの法則はこの左辺と右辺が等しいと主張しているので、両辺同じ単位になるはずです。 そのため、$\rm{Dm^2=C}$を$\rm{D}$について解くことで$\rm{D=Q/m^2}$クーロン毎平方メートルが出てきます。 以上から、イの答えは4.クーロン毎平方メートル$\rm{D=Q/m^2}$です。ウ
透磁率が出てくる式はいろいろありますが、選択肢にはご丁寧にヘンリー[H]が含まれる式があるのでこれに当たりをつけて考えてみましょう。 インダクタンスの表式は \[L=\mu \frac{N^2 S}{l}\] で書けます。 これを$\mu$について解くと \[ \mu=\frac{L l}{N^2 S} \] となります。 文字の定義は- $L$:インダクタンス[\rm{H}]
- $N$:コイルの巻数[無次元]
- $l$:コイルの長さ[$\rm{m}$]
- $S$:コイルの断面積[$\rm{m^2}$]
エ
導電率は抵抗率の逆数です。 抵抗率を$\rho$導体の断面積を$S$、長さを$l$としたときに抵抗が$R=\rho\frac{l}{A}$で表されます。 導電率$\sigma$は$\sigma=1/\rho=\frac{l}{RA}[\rm{\frac{1}{\Omega m}}]$です。 抵抗の逆数の単位はジーメンス[\rm{S}]なのでエは3.ジーメンス毎メートル$\rm{S/m}$です。オ
誘電率の単位はは$D=\epsilon E$の関係式が成り立つので、イの答えを使って \[ \rm{\frac{C}{m^2}\frac{m}{V}}=\rm{C/V/m}=\rm{F/m} \] となります。 以上から、オの答えは2.ファラド毎メートル$\rm{F/m}$です。R.3.12 無線工学 B-2
水晶発振器に関する問題です。 正しいか誤りか選ぶ問題なので1つずつ見ていきましょう。ア
VCXOは問題文の通りで、可変容量ダイオードによって共振周波数を変える水晶発振器です。 アは正しいので答えは1です。イ
TCXOは問題文の通りで、水晶片の温度係数を打ち消す素子で温度変化を補正して共振周波数を暗転させる水晶発振器です。 イは正しいので答えは1です。ウ
OCXOは水晶発振回路を恒温槽に入れて周囲温度の影響を受けないようにした水晶発振器です。 恒温槽の温度が安定するまでは周波数は安定しないので安定するのに時間がかかるのがOCXOの特徴です。 もちろん、TCXOと比較してもOCXOの方が周波数が安定するまで時間がかかります。 そのため、ウは誤っているので答えは2です。エ
VCXOやTCXOは周囲温度の影響を補正しているだけなのに対して、OCXOは温度を周囲より高くして、水晶発振回路が常に同じ温度で周囲からの影響をなくしています。 その分OCXOが最も周波数精度は良くなります。 そのため、エは誤っているので答えは2です。オ
問題文の通りでルビジウム発振器ルビジウムの固有周波数に水晶発振器の発振周波数を同期させたものです。 オは正しいので答えは1です。R.3.12 無線工学 B-3
整流回路に関する問題です。ア
この回路は電流が正でも負でも負荷抵抗に電流が流れるので全波整流回路です。 そのため、アには5.「全波」が入ります。イ
全波整流回路の波形は図のようになります。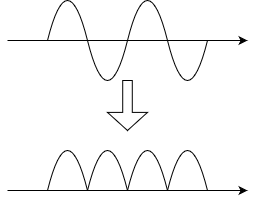
全波整流回路の波形
ウ
実効値は \[ I_r=\sqrt{\frac{1}{2\pi}\int^{2\pi}_0I^2(t)d(\omega t)} \] で計算できます。 ルートの中身をまず計算しましょう。 \[ \frac{1}{2\pi}\int^{2\pi}_0I^2(t)d(\omega t)=\frac{1}{2\pi}\int^{2\pi}_0I_m^2\sin ^2(\omega t)d(\omega t) \\ =\frac{1}{2\pi}\int^{2\pi}_0I_m^2\frac{1}{2}(1-\cos 2\omega t)d(\omega t) \\ =\frac{I_m^2}{2\pi}(\pi – 0) \\ =\frac{I_m^2}{2} \] 計算結果をルートに入れると$\frac{I_m}{\sqrt{2}}$になります。 そのため、答えは3.$\frac{I_m}{\sqrt{2}}$です。エ
波形率は$frac{\rm{実効値}}{\rm{平均値}}$で表せます。 イとウの結果から$\frac{\pi}{2\sqrt{2}}=1.11$です。 そのため、答えは9.の1.11です。オ
可動コイル形電流計の指示値は電流の平均値です。 そのため$I_m=\frac{\pi}{2}\times 1=1.57[mA]$となります。 オの答えは7. の1.57です。R.3.12 無線工学 B-4
短波帯のフェージングの軽減方法に関する問題です。ア
受信機の入力段には受信電界強度の変動を補償するAGC回路を設けることがあります。 AGCはAutomatic Gain Cotrolの略で、自動で利得を調整して、受信電界強度の変動を吸収する回路です。 そのため、アには2.「AGC」が入ります。イ
無線電信にはリミタを入れて検波出力の振幅をそろえます。 そのため、イには3.「リミタ」が入ります。ウ
搬送波と側波帯に一様なフェージングがある場合、AGCはその影響を軽減できます。 AGCは受信帯域全体の利得を自動で変化させる回路なので、変動が一様な場合はその変動に合わせて利得を調整し、変動を補正できます。 そのため、ウには9.「できる」が入ります。エ
エとオは回路ではなくダイバーシティ技術に関する記述です。 エでは周波数を2つ以上同時に送信する手法なので周波数ダイバーシティのことを説明しています。 この方式は狭帯域な信号に対する周波数に依存したフェージングに対して特に効果があります。 エには6.「周波数」が入ります。オ
オは受信点の位置を複数にする手法なので空間ダイバーシティについて説明しています。 空間ダイバーシティは電波の伝播経路などに起因するフェージングに対して特に効果があります。 オには5.「空間」が入ります。R.3.12 無線工学 B-5
送信設備の「スプリアス発射の強度」や「不要発射の強度」の測定方法に関する問題です。 アマチュア無線に関係したアマチュア無線技士の試験らしい問題です。ア、イ
帯域外で中心周波数から$\pm 2.5B_N$以内の領域を「帯域外領域」、中心周波数から見て帯域外領域の外側の領域を「スプリアス領域」と呼びます。 そのため、アには1.「帯域外領域」、イには6.「スプリアス領域」が入ります。ウ
不要発射の強度の測定は変調状態で行います。 もし、このことを覚えていなくても、その後ろの文に必要周波数帯域幅という言葉があるので、変調波を使うことは予想できるでしょう。 そのため、ウには4.「変調」が入ります。エ
SSBの変調信号に擬似音声を使う時は1500[Hz]の正弦波で空中線電力が飽和レベルの80%程度となる変調入力電圧を使います。 ここは覚えるしかないでしょう。 そのため、エには10.「80」が入ります。オ
電信の電鍵操作では25ボーの連続短点を使います。 ここも覚えるしかないでしょう。 そのため、オには8.「25ボーの連続短点」が入ります。まとめ
最近、難化傾向と言われる1アマの問題を解いてみました。 1陸技と比べると基本的な問題が出ますが、たしかに私が受けた10年前より難しくなっている気もします。 今週1陸技の試験があったので、また問題がアップロードされ次第、R4年1月分の1陸技の無線工学の問題を解いていこうと思います。 9月の1総通の試験を目指して勉強を開始するので、需要がありそうなら英語や地理の問題も解いて記事にさせていただくかもしれません。 無線工学については免除なので解かない予定です。 個人的には私のように実務経験で取得しない場合は、1陸技→1総通のルートの方が王道なのではないかと思います。 勉強法 第一級陸上無線技術士の勉強法とおすすめ参考書参考文献
リンク
電磁気学をちゃんと学びたい人向け
リンク
上の難易度が高い人
リンク
リンク


コメント