令和3年7月の1陸技の試験、無線工学BのB-1~5の問題について解説します。 最後の5問は選択肢が多かったり、消去法が使いにくかったりするような小手先では解きにくい問題が出題されます。 焦らず問題文をしっかり読めば解くことができるでしょう。
R.3.7 無線工学B(1回目) B-1

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B B-1
パラボラアンテナの問題です。幾何学的なことが分かっているかを問う問題になっています。
ア
放物線の定義は準線からの距離と焦点からの距離が等しい点の集まりです。 そのため、任意の点Pでは$\bar{\rm{PQ}}=\bar{\rm{FP}}$となります。
以上から答えは1.$\bar{\rm{FP}}$です。
イ
アの結果から次のようになります。 \[ \bar{\rm{FP}}+\bar{\rm{PS}}=\bar{\rm{PQ}}+\bar{\rm{PS}}=\bar{\rm{QS}} \]
以上から答えは2.$\bar{\rm{QS}}$です。
ウ
任意の点Pで$\bar{\rm{FP}}+\bar{\rm{PS}}=\bar{\rm{QS}}$が成り立つので、焦点Fの等方性波源から放射された電波は見かけ上平面Gを波源とした平面波として扱えます。
そのため、答えは8.波源です
エ
平面Hは見かけ上の波源である平面Gから等距離な点の集まりなので、同位相になります。
そのため、答えは4.同位相です。
オ
ここでは$\triangle{\rm{FPS}}$を考えます。 $\angle{\rm{FPS}}=\theta$なので、$\bar{\rm{PS}}=\bar{\rm{FP}}\cos \theta$となります。
この結果を与えられた式に代入すると$\bar{\rm{FP}}+\bar{\rm{PS}}=\bar{\rm{FP}}(1+\cos \theta)$となります。
そのため、答えは10.$1+\cos \theta$です。
R.3.7 無線工学B(1回目) B-2

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B B-2
方形導波管に関する問題です。
ア
遮断波長の式を問う問題です。 遮断波長は$\frac{2\sqrt{\epsilon_r \mu_r}}{\sqrt{\left(\frac{m}{a}\right)^2+\left(\frac{n}{b}\right)^2}}$で表せます。 この式の導出はここに書くとかなり重いの別記事でまとめたいと思います。
ここでは真空を考えているので$\epsilon_r \mu_r=1$です。
そのため答えは6.$\frac{2}{\sqrt{\left(\frac{m}{a}\right)^2+\left(\frac{n}{b}\right)^2}}$です。
イ
ここでは$\rm{TE_{10}}$を考えるの$m=1, n=0$なのでアの式に代入すると$2a$となります。
そのため、答えは7.$2a$です。
ウ
管内波長$\lambda_g$は遮断波長$\lambda_c$を使って$\lambda_g=\frac{\lambda}{\sqrt{1-\left(\frac{\lambda}{\lambda_c}\right)^2}}$なので、イの結果を代入して、 \[ \lambda_g=\frac{\lambda}{\sqrt{1-\left(\frac{\lambda}{2a}\right)^2}} \] となります。
以上から答えは3.$\lambda_g=\frac{\lambda}{\sqrt{1-\left(\frac{\lambda}{2a}\right)^2}}$です。
エ
位相速度$v_p$は$v_p=f\lambda_g=\frac{c}{\sqrt{1-\frac{\lambda}{\lambda_g}}}$、群速度$v_g$は$v_g=c\sqrt{1-\frac{\lambda}{\lambda_g}}$と表せます。 この導出もアと同様、別記事でまとめたいと思います。
$\sqrt{1-\frac{\lambda}{\lambda_g}} < 1 $なので、$v_p > c > v_g$です。
そのため、エには9.遅くが入ります。
オ
先ほどの$v_p, v_g$の定義から$v_pv_g=c^2$です。
そのため、オには5.$v_pv_g=c^2$が入ります。
R.3.7 無線工学B(1回目) B-3

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B B-3
ヘリカルアンテナ(エンドファイアヘリカルアンテナ)に関する問題です。
ア
ヘリカルアンテナではヘリックス1巻きの長さが1波長に近づくと電流は軸に沿った進行波になります。
そのため、アには1.進行波がはいります。
イ
電流が進行波として、先端に向かいながら電波として放射されるので、軸方向に指向性を持ちます。
そのため、イにはは7.軸方向が入ります。
ウ
ヘリカルアンテナでは軸方向に磁界が発生し、電流は軸に垂直な方向になります。 1巻き内の電流分布は時間によって変化し、電界の方向が1周期で1回りします。 そのため、偏波は円偏波になります。
そのため、ウには3.円偏波が入ります。
エ
ヘリックスの巻数を少なくすると指向性が小さくなります。 指向性が小さくなると、半値角は大きくなります。
そのため、エには4.大きくが入ります。
オ
入力インピーダンスが一定となる範囲が広いほど使用周波数帯域が広いと言えます。
そのため、オには10.広くなるが入ります。
R.3.7 無線工学B(1回目) B-4

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B B-4
ダイバーシティ方式について正誤を選ぶ問題です。消去法は使えませんが、それぞれの選択肢を精査しながら解いていきましょう。。
ア
この記述は正しい記述で、答えは1です。
イ
スペースダイバーシティは異なる受信点間のフェージングの差を使ってフェージング対策をします。 受信点間の電界強度変動の相関が大きいということはフェージングの差が小さいので効果は小さくなります。
そのため、この記述は誤りで答えは2です。
ウ
偏波ダイバーシティでは異なる偏波のアンテナの差を使ってフェージングを対策します。 ダクト性フェージングでは偏波ごとにフェージングに差が生じないのでダクト性フェージングに偏波ダイバーシティはあまり効果がありません。
そのため、この記述は誤りで答えは2です。
エ
この記述は正しい記述で、答えは1です。
オ
この記述は正しい記述で、答えは1です。
R.3.7 無線工学B(1回目) B-5
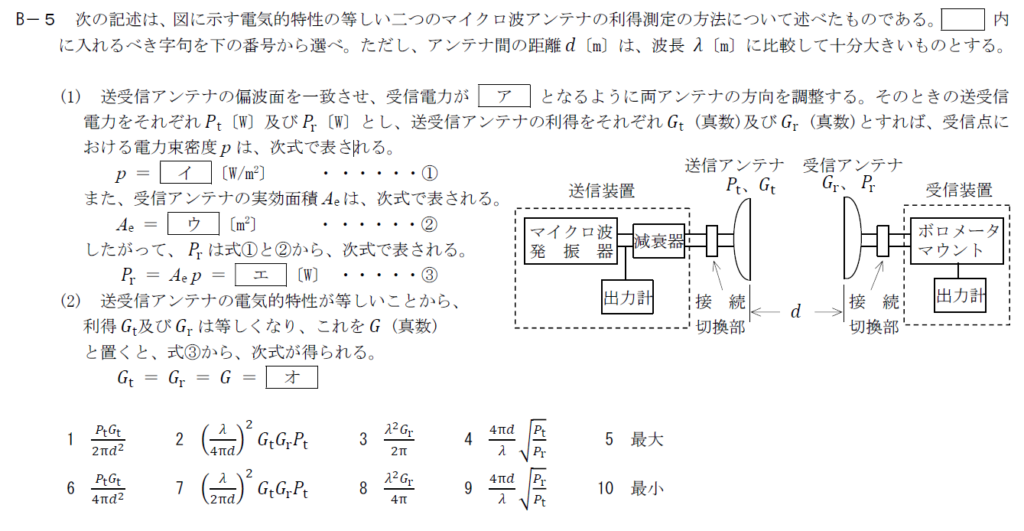
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B B-5
マイクロ波アンテナの利得測定の方法に関する問題です。
ア
利得は受信(送信)電力が最大になる方向で定義するのでアには5.最大が入ります
イ
利得$G_t$のアンテナから放射された電波は距離d[m]離れた受信点では$\frac{P_tG_t}{4\pi d^2}$と表されます。 送信点から等方的放射されたとすれば、距離d[m]離れた点の単位面積あたりの電力は$\frac{P_t}{4\pi^2}$です。 利得が$G_t$(真数)のアンテナから放射しているので$G_t$倍すれば求まります。
以上から、イには6.$\frac{P_tG_t}{4\pi d^2}$が入ります。
ウ
実効面積は$\frac{\lambda^2 G_r}{4\pi}$と表せます。
そのため、ウには8.$\frac{\lambda^2 G_r}{4\pi}$が入ります。
エ
イとウと掛け算すれば求まります。
そのため、エには2.$\left(\frac{\lambda^2}{4\pi d}\right)^2G_tG_rP_t$が入ります。
オ
エの式に$G_t=G_r=G$として、$G$について解くと$G=\frac{4\pi d}{\lambda}\sqrt{\frac{P_r}{P_t}}$となります。
そのため、エには9.$\frac{4\pi d}{\lambda}\sqrt{\frac{P_r}{P_t}}$が入ります。
まとめ
今回は先日行われた令和3年7月1回目の1陸技の無線工学BのB-1~5を解いてみました。 A-の問題と比べると計算が必要で1つ間違えるとそれ以降すべて間違える可能性がある問題もあります。 難しく構えず、冷静に解けばそれほど難しい問題ではありません。
過去問が多く出題される1陸技の試験ですが、ここ最近は1回の試験で2回分の過去問が出るので過去問もはかどりますね。 試験が終わった直後ですが、次の試験を目指すならこの時期からであれば次の試験まで十分に時間が取れます。 1陸技を目指す方は頑張っていきましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人


コメント