令和3年7月の1陸技の試験2回目の無線工学BのA-6~10の問題について解説します。
R.3.7 無線工学B(2回目) A-6

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学B A-6
同軸ケーブルの特性インピーダンスに関する問題です。 具体的な形まではいいかもしれませんが、同軸ケーブルの特性インピーダンスの計算式は覚えていないと解けない問題です。
同軸ケーブルの特性インピーダンス$Z_0$は \[ Z_0=\frac{138}{\sqrt{\epsilon_r}}\log \frac{D}{d} \] です。 $\epsilon_r$は誘電体の比誘電率、$D$は外部導体の内径、$d$は内部導体の外径です。
問題文から$D/d=4$、外部導体の内径を2倍にするので$D/d=8$となります。 $\log 4=2\log 2, \log 8=3\log 2$です。
外部導体の内径を変更する前後の特性インピーダンスをそれぞれ$Z_0,Z_0’$としましょう。 \[ Z_0=\frac{138}{\sqrt{\epsilon_r}} \times 2\log 2 =50 \\ Z_0’=\frac{138}{\sqrt{\epsilon_r}} \times 2\log 3 \] なので、2式の比を取って$Z_0’/50=3/2$です。 計算すると$Z_0’=75[\rm{\Omega}]$となります。
そのため、答えは5です。
R.3.7 無線工学B(2回目) A-7
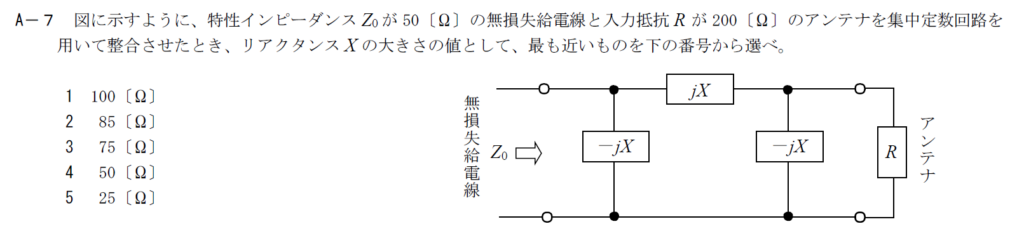
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学B A-7
$\pi$型整合回路に関する問題です。
給電線から見たインピーダンスを計算すると$\frac{X^2}{R}$となるので、このインピーダンスが給電線の特性インピーダンス50$\rm{[\Omega]}$と等しくなります。 $X$について解くと$X=100\rm{[\Omega]}$となります。
そのため、答えは1です。
R.3.7 無線工学B(2回目) A-8

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学B A-8
終端を短絡した平衡二線式給電線のインピーダンスに関する問題です。 こちらも線路のインピーダンスを覚えておいたほうが良いでしょう。 計算はそのうち別記事にしたいと思います。
平衡二線式給電線の特性インピーダンス$Z_0$は$Z_0=276\log \frac{2D}{d}$で表されます。 $D$は線間隔、$d$は線の直径です。
問題の条件を代入すると$Z_0=276\log \frac{40\times 10^{-2}}{4\times 10^{-3}}=276 \times 2$です。
一方、終端を短絡した二線式給電線の終端から長さ$l$の位置でのインピーダンスは$Z=jZ_0\tan( \frac{2\pi}{\lambda}l)$と表されます。 この問題では周波数が15MHzなので$\lambda=20$[m]、$l=2.5$[m]なので$Z=jZ_0$となります。
コイルのインダクタンスが$j\omega L$であり、これと$Z$が等しくなる時の$L$が求めるインダクタンスです。
\[ L=\frac{Z_0}{2\pi f}=5.85 \times 10^{-6}[\rm{H}]\simeq 5.9[\rm{\mu H}] \]
答えは4です。
R.3.7 無線工学B(2回目) A-9

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学B A-9
導体への電磁波の侵入する時の表皮厚さに関する問題です。 それぞれの選択肢を見ていきましょう。
1
電界、磁界、電流が1/eになる表面からの距離が表皮厚さの定義です。 この選択肢は正しいです。
2
表皮厚さ$d$は$d=\sqrt{\frac{2}{\omega \mu \sigma}}$と表されます。 ここで$\omega=2\pi f$、$\mu$は透磁率、$\sigma$は導電率です。
この式から透磁率が小さいほど表皮厚さは厚くなります。 そのため、この選択肢は正しいです。
3
導電率が小さいほど表皮は厚くなりますのでこの選択肢が誤りです。
4
減衰定数が小さいほど内部に電磁波が侵入しやすいので、表皮厚さは厚くなります。 そのため、この選択肢は正しいです。
5
周波数が高くなると表皮は薄くなるのでこの選択肢は正しいです。
以上から答えは3です。
R.3.7 無線工学B(2回目) A-10

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月2回目 無線工学B A-10
コーナレフレクタアンテナに関する問題です。
A
開き角が90°の時は1回反射と2回反射の鏡像があり、ダイポールアンテナ本体と合わせて4個のダイポールがあるように動作します。
鏡像の位置を図に示します。ばつ印は位相が反転している鏡像(1回反射)です。
そのためAには4個が入ります。

開き角が90°のときの鏡像位置
B
開き角が60°のときも同様に考えます。
鏡像の位置を図に示します。ばつ印は位相が反転している鏡像(1回反射)です。
このときはダイポールの鏡像は5個あるため、Bには6個が入ります。

開き角が60°のときの鏡像位置
C
開き角が45°のときは7個の鏡像があるため、Cには8個が入ります。
鏡像の位置を図に示します。ばつ印は位相が反転している鏡像(1回反射)です。
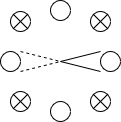
開き角が45°のときの鏡像位置
D,E
開き角90°のコーナレフレクタアンテナでは反射板による鏡像効果で4本のダイポールアンテナが配列されたような動作をします。
ダイポールアンテナの配列に関する考察は別記事にしたいと思います。 まず、2個のダイポールアンテナの配列の指向性係数を考えます。 この時の指向性係数は \[ D=2\cos \left\{ \frac{1}{2}(\delta -\frac{2\pi}{\lambda}d’\cos \phi)\right\} \] です。 $\delta$はダイポールアンテナ間の位相差、$\phi$はアンテナ配列から受信点への角度です。
コーナレフレクタアンテナでは同一直線上にあるダイポールアンテナの位相差は$\delta =2\pi$です。
$d$については選択肢にある$\lambda$と$3\lambda /2$を考えましょう。 折り目からの距離の2倍が$d’$となります。 $d=2\lambda$のときは$D=-2\cos (2\pi \cos \phi)$、$d=3\lambda$のときは$D=-2\cos (3\pi \cos \phi)$となります。
開き角が90°の鏡像の配置を考えると上記の2個の配列が逆位相で直角に配置されています。 折り目からの距離が$d=\lambda$($d’=2\lambda$)のときは2つの配列でいずれも$D=-2$となり、それぞれ逆位相なので打ち消し合います。 このことは主ビームが2つに割れることを意味します。
そのため、主ビームが2つに割れるのは$d=\lambda$の時です。
折り目からの距離が$d=3\lambda /2$($d’=3\lambda$)のときは、$D=-2$と$D=+2$となり、逆位相なのでそれぞれ強め合います。
そのため、主ビームが鋭くなるのは$d=3\lambda /2$のときです。
以上から答えは2です。
まとめ
今回は先日行われた令和3年7月2回目の1陸技の無線工学BのA-1~5を解いてみました。 過去問が多く出題される1陸技の試験ですが、ここ最近は1回の試験で2回分の過去問が出るので過去問もはかどりますね。 次の試験を目指すならこの時期からであれば次の試験まで十分に時間が取れます。 1陸技を目指す方は頑張っていきましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人


コメント