令和5年7月の1陸技の試験1回目の無線工学AのA-11~15の問題について解説します。
R.5.7 無線工学A(1回目) B-1

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学A B-1
電力増幅器に関する問題です。
この問題は問題文が全く同じ問題が令和3年7月2回目A-16で出題されています。
下記の記事をご参照ください。

ア
相互変調積が発生するのは増幅器の非線形領域を使用した時に信号が歪むためです。 非線形領域は電力効率がよくするため使用されます。
そのため、アには6.「非線形」が入ります。
イ
これは令和3年7月2回目A-16のAの空欄に相当します。
相互変調積により異なる周波数成分が生じます。 相互変調積により出力された信号分、帯域内の各波の電力は減少するので帯域内の飽和出力電力の総和は減少します。
そのため、イには1.「総和は減少する」が入ります。
ウ
これは令和3年7月2回目A-16のBの空欄に相当します。
入力バックオフは単一はを入力したときの飽和入力電力と複数は全入力電力の比です。
そのため、ウには8.「入力電力」が入ります。
エ
これは令和3年7月2回目A-16のCの空欄に相当します。
相互変調積は非線形領域で生じるので入力バックオフが大きくなるほど相互変調積に対して余裕があることになります。
そのため、エには3.「大きく」が入ります。
オ
入力バックオフが大きいということは線形領域を使用することを意味します。 この場合、非線形領域を使用する場合と比べて電力利用効率が低下します。
そのため、オには5.「電力利用効率」が入ります。
R.5.7 無線工学A(1回目) B-2
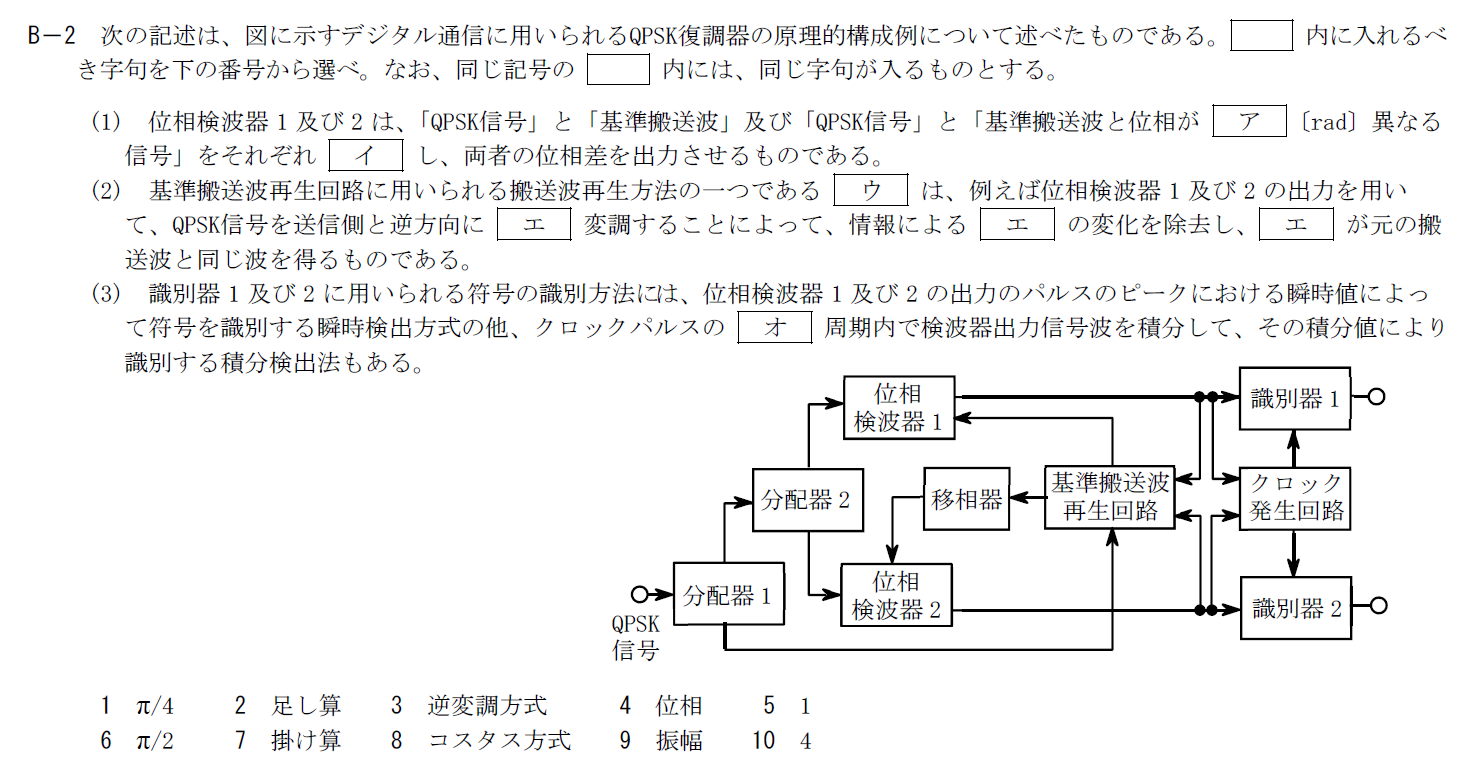
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学A B-2
QPSK復調器に関する問題です。
この問題は空欄を含めて全く同じ問題が令和4年1月1回目B-4で出題されています。
下記の記事をご参照ください。

答えは
- ア:6.「$\pi /2$」
- イ:7.「掛け算」
- ウ:3.「逆変調方式」
- エ:4.「位相」
- オ:5.「1」
です。
R.5.7 無線工学A(1回目) B-3
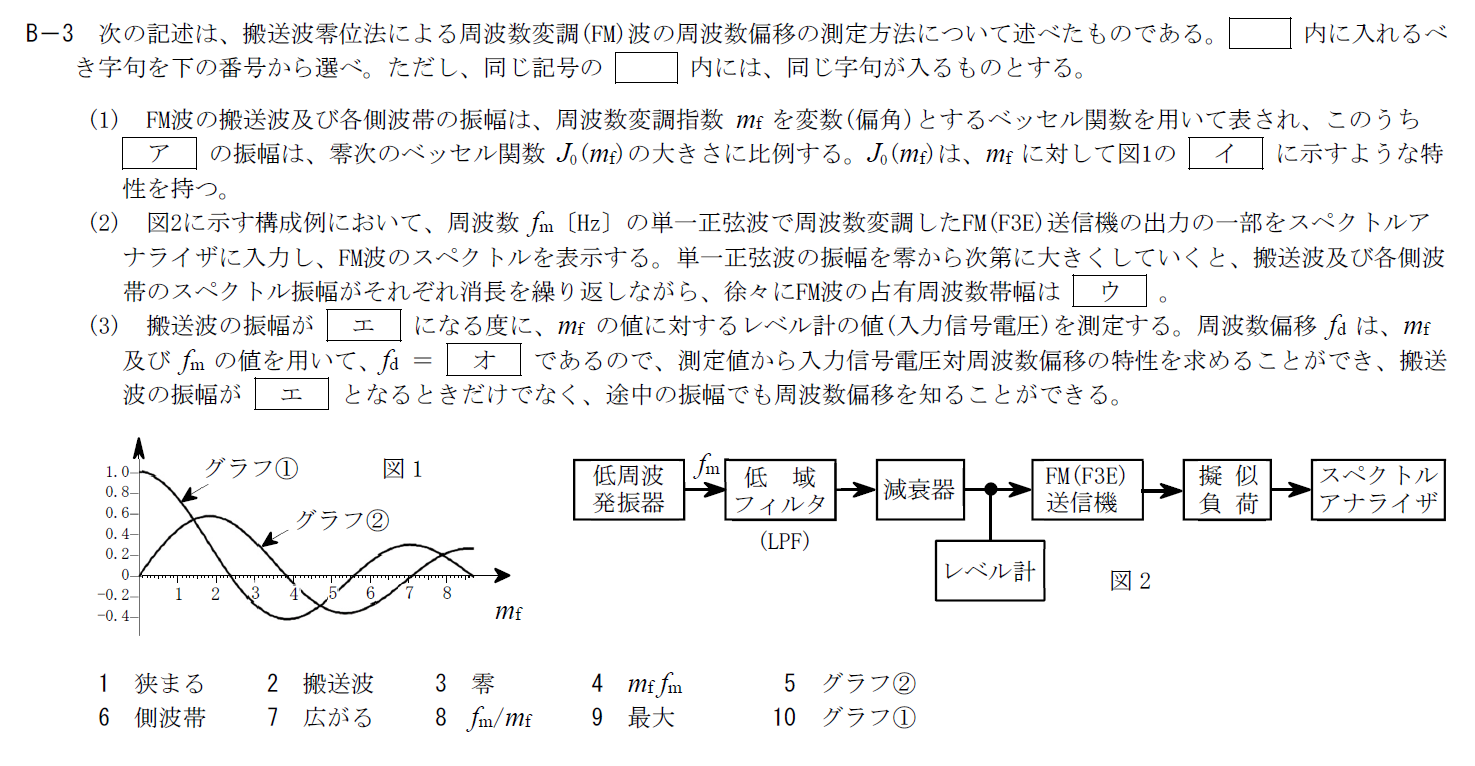
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学A B-3
FMの位相偏移の測定方法に関する問題です。
この問題は空欄を含めて全く同じ問題が令和4年1月2回目B-2で出題されています。
下記の記事をご参照ください。

答えは
- ア:2.「搬送波」
- イ:10.「グラフ①」
- ウ:7.「広がる」
- エ:3.「零」
- オ:4.「$m_ff_m$」
です。
R.5.7 無線工学A(1回目) B-4
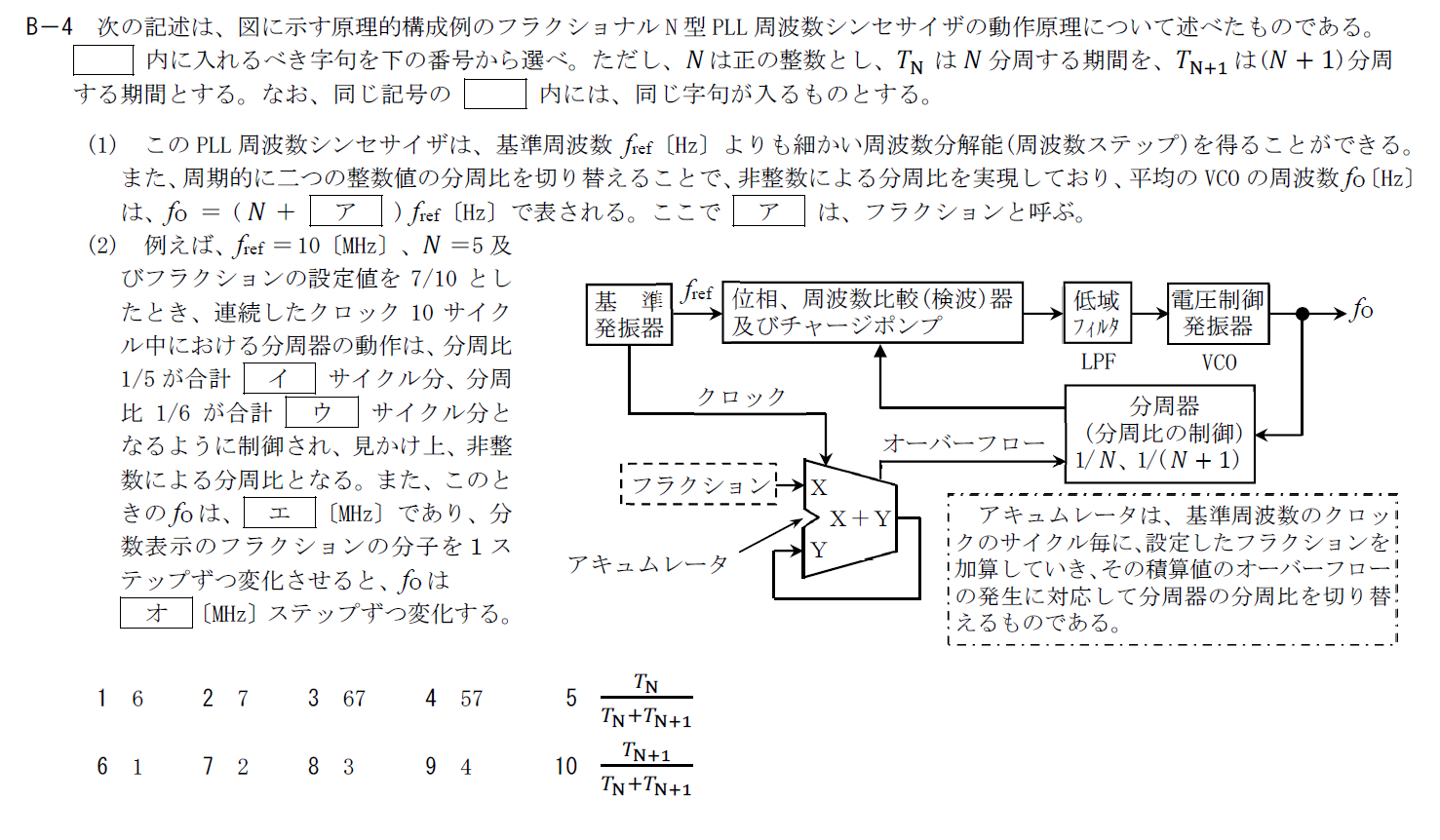
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学A B-4
フラクショナルN型PLL周波数シンセサイザに関する問題です。
同様の問題が令和4年7月1回目A-19で出題されています。 空欄の位置と計算に使う値が違うので気を付けましょう。
ア
分周比が$1/N$の時VCOの出力が$f_O=Nf_{ref}$となり、$1/(N+1)$の時VCOの出力が$f_O=(N+1)f_{ref}$となります。
これらの分周比が$T_N$と$T_{N+1}$で切り替えられると \[ f_O=\frac{T_N}{T_N+T_{N+1}}Nf_{ref}+\frac{T_{N+1}}{T_N+T_{N+1}}(N+1)f_{ref} \\ =\frac{NT_N+(N+1)T_{N+1}}{T_N+T_{N+1}}f_{ref} \\ =\left\{N+\frac{T_{N+1}}{T_N+T_{N+1}}\right\}f_{ref} \] となります。
そのため、アには10.「$\frac{T_{N+1}}{T_N+T_{N+1}}$」が入ります。
イ、ウ
問題文から \[ \frac{T_{N+1}}{T_N+T_{N+1}}=7/10 \] なので、この式を変形すると \[ \frac{T_N}{T_{N+1}}=\frac{3}{7} \] となります。
そのため、イには8.「3」、ウには2.「7」が入ります。
エ
$\frac{T_{N+1}}{T_N+T_{N+1}}=7/10$を$f_O$の式に代入すると \[ f_O=\left\{5+\frac{3}{10}\right\}\times 10 =57\rm{[MHz]} \] となります。
そのため、エには4.「57」が入ります。
オ
フラクションの分子が10なので、$f_{ref}$の$1/10$が1ステップ分の周波数$1\rm{[MHz]}$になります。
そのため、オには6.「1」が入ります。
R.5.7 無線工学A(1回目) B-5

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学A B-5
FMにおけるエンファシスの原理に関する問題です。
この問題はプレエンファシス回路を扱っており、ディエンファシス回路の問題が令和3年7月1回目B-5で出題されています。
下記の記事も一緒に参考にしてください。

ア
FMでは変調器に起因する雑音は三角雑音とも呼ばれ、高域成分が強くなります。 一方でFMの変調信号としてよく使用される音声などは高域成分が少ないことが多いです。
このような事情から高域のS/Nが悪くなるため、送信側でハイパスフィルタを使用することで高域成分を強調し、受信側で逆の周波数特性のローパスフィルタを通すことで元の信号に戻すという操作をします。 前者をプレエンファシス、後者をディエンファシスと言います。
上記の内容から分かるようにアには1.「高域成分」が入ります。
イ
回路図から$e_2$を求めてみましょう。 \[ e_2=\frac{R_2}{(j\omega C+1/R_1)^{-1}+R_2}e_1 \\ =\frac{R_2}{R_1(j\omega \tau +1)^{-1}+R_2}e_1 \\ =\frac{R_2(1+j\omega \tau)}{R_1+R_2(1+j\omega \tau)}e_1 \\ \]
この結果の分母がイに入るのでイには7.「$R_1+R_2(1+j\omega \tau)$」が入ります。
ウ
$\omega =0$を代入して$e_{20}=\frac{R_2}{R_1+R_2}e_1$なので \[ F_p(\omega )=e_2/e_{20} \\ =\frac{R_2(1+j\omega \tau)}{R_1+R_2(1+j\omega \tau)}\frac{R_1+R_2}{R_2} \\ =\frac{1+j\omega \tau}{\frac{R_1+R_2+j\omega \tau R_2}{R_1+R_2}} \\ =\frac{1+j\omega \tau}{1+j\omega \tau \frac{R_2}{R_1+R_2}} \] となります。
ウにはこの式の分母が入るので、ウには9.「$[1+j\omega \tau \{R_2/(R_1+R_2)\}]$」が入ります。
エ
まず、$\alpha =\omega \tau \frac{R_2}{R_1+R_2}$と置きます。問題文から最終的に$\alpha \rightarrow 0$の極限をとることになります。 極限をとりやすい形に変形しておきます。 \[ F_p(\omega )=\frac{1+j\omega \tau}{1+j\alpha} \\ =\frac{(1+j\omega \tau)(1-j\alpha)}{1+\alpha^2} \\ =\frac{1+\omega \tau \alpha +j(\omega \tau -\alpha)}{1+\alpha^2} \]
$|F_p(\omega )|$を計算します。 \[ |F_p(\omega )|=\frac{1}{1+\alpha^2}\sqrt{(1+\omega \tau \alpha)^2+(\omega \tau -\alpha )^2} \\ =\frac{1}{1+\alpha^2}\sqrt{(1+(\omega \tau)^2+(1+\omega \tau )\alpha^2} \] ここで$\alpha \rightarrow 0$とすると \[ |F_p(\omega )|=\sqrt{1+(\omega \tau )^2} \] となります。
そのため、エには5.「$\sqrt{1+(\omega \tau )^2}$」が入ります。
オ
ディエンファシス回路はプレエンファシス回路と逆の周波数特性を持ちます。 そのため、 \[ |F_d(\omega )|=1/|F_p(\omega )|=1/\sqrt{1+(\omega \tau )^2} \] となります。
オには3.「$1/\sqrt{1+(\omega \tau )^2}$」が入ります。
まとめ
今回は令和5年7月の無線工学A(1回目)の試験B-1~B-5の問題について解説しました。 B問題は比較的過去問が出題されやすく今回も同様でした。
解説のため丁寧に計算していますが、本番の試験ではエッセンスだけ押さえておけば丁寧に計算する必要はありません。
勉強法についてはこちらも参考にしてください。 おすすめの勉強法や参考書を紹介しています。

参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント