令和3年7月の1陸技の試験、無線工学BのA-1~5の問題について解説します。
R.3.7 無線工学B(1回目) A-1

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B A-1
毎年出題されるマクスウェル方程式のサービス問題です。
A
マクスウェル方程式で時間微分が入る式はアンペアの法則とファラデーの電磁誘導の法則だけです。 これらの式のAの部分には$\nabla\times$が入ります。
B
①の右辺に③を代入すれば計算できます。 ここでの答えは$(\sigma+j\omega\epsilon)E$です。
C
ここも代入すれば答えが出ます。 ここでの答えは$-j\omega\mu H$です。
したがって答えは5です。
R.3.7 無線工学B(1回目) A-2

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B A-2
この問題は単なる計算問題です。
計算が面倒くさいだけなので早く正確に計算できる練習をしておきましょう。
$\theta_E$および$\theta_H$をラジアンに直すと \[ \theta_E=\frac{\pi}{60} \] \[ \theta_H=\frac{\pi}{72} \]です。
次に$G_d$の真数を求めましょう。
\[G_d=\frac{4\pi}{\frac{1}{60}\frac{1}{72}\pi^2}=\frac{17280}{\pi}=5503\] \[ 10\log G_d=10\log(5.5\times10^3)=7.4+30=37 \]
以上から答えは2です。
R.3.7 無線工学B(1回目) A-3

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B A-3
用語の問題です。
A
問題文の内容から可逆定理です。
B
問題文の内容から配列指向係数(アレーファクタ)です。
C
こちらも覚えているかどうかの問題ですが、真数で覚えているというよりdBで覚えている人が多いのではないでしょうか。 半波長ダイポールアンテナの絶対利得は2.15[dBi]であることから考えるのが良いでしょう。 わからなければ選択肢が2つしかないので代入してみるのが早いでしょう。 対数をけいさんするのは大変なので一般的な値($\log2=0.3$や$\log3=0.48$)からざっくり計算してもっともらしい方を選びます。 \[10\log(0.61)\simeq 10\log(0.6)=10(\log2+\log3-1)=-2.22\] \[10\log(0.91)\simeq 10\log(0.9)=10(2\log3-1)=-0.46\] この結果から答えは0.61です。
以上から答えは3です。
R.3.7 無線工学B(1回目) A-4
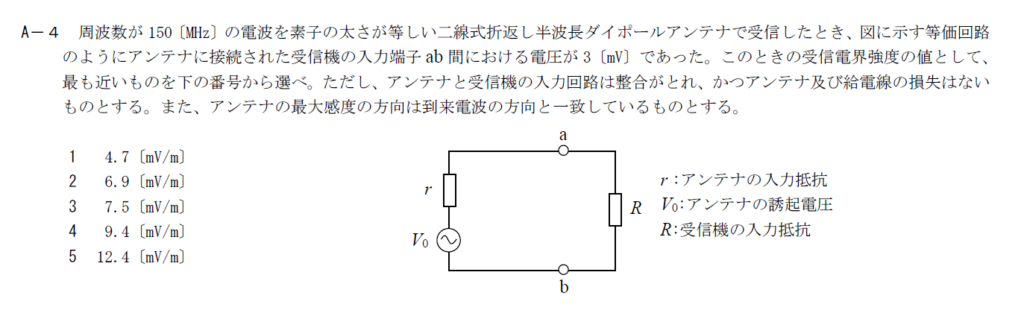
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B A-4
折返し半波長ダイポールアンテナの実効長$l_e$は半波長ダイポールアンテナの2倍なので \[ l_e=\frac{2\lambda}{\pi} \] です。
そのため受信電界強度を$E$とすると、アンテナ端子には$V=El_e=\frac{2E\lambda}{\pi}$の電圧が誘起されます。
アンテナと受信機は整合が取れているので$R=r$となっています。
そのため、ab間の電圧$V_{ab}$は$V_{ab}=V/2$となります。
以上から$V_{ab}=\frac{E\lambda}{\pi}$となるので$E=\frac{V_{ab}\pi}{\lambda}=4.7[mV/m]$です。
ゆえに答えは1です。
R.3.7 無線工学B(1回目) A-5

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B A-5
問題文中にある3つの成分はそれぞれ下記に比例します。
- 放射電界:$|E_1|=\frac{1}{r}$
- 誘導電界:$|E_2|=\frac{\lambda}{2\pi r^2}$
- 静電界:$|E_3|=\frac{\lambda^2}{4\pi^2 r^3}$
A
誘導電界と静電界が放射電界と等しくなる$r$を求めていきましょう。 いずれも同じ値で$r=\frac{\lambda}{2\pi}$となります。 $r$がこの値より大きいときは放射電界が最も大きくなり、小さいときは静電界が最も大きくなります。
B
$r=0.01\lambda$はAで求めた$r=\frac{\lambda}{2\pi}$より小さいので$|E_3|$が最も大きくなります。 選択肢から考えて$|E_3|$が1になるように計算する方針で行きましょう。 \[ |E_1|:|E_2|:|E_3|=4\pi^2\times 0.01^2:2\pi \times 0.01:1=0.0039:0.063:1 \] となります。
以上から答えは4です。
まとめ
今回は先日行われた令和3年7月1回目の1陸技の無線工学BのA-1~5を解いてみました。 過去問が多く出題される1陸技の試験ですが、ここ最近は1回の試験で2回分の過去問が出るので過去問もはかどりますね。 試験が終わった直後ですが、次の試験を目指すならこの時期からであれば次の試験まで十分に時間が取れます。 1陸技を目指す方は頑張っていきましょう。 勉強法
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人


コメント