令和4年1月の1陸技の試験2回目の無線工学BのB-1～5の問題について解説します。
R.4.1 無線工学B（2回目） B-1
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B B-1
2本の半波長ダイポールアンテナから成るアンテナ系の利得を求める問題です。
問題文が誘導してくれているのでそれに従って穴埋めしていきましょう。
ア
半波長ダイポールアンテナ1個の入力インピーダンスは自己インピーダンスと相互インピーダンスが直列に接続されているように見えるので
\[
Z_i=Z_{11}+Z_{12}
\]
となります。
そのため、アには2.「$Z_{11}+Z_{12}$」が入ります。
イ
(2)の記述ではアンテナAだけを接続するので$Z_i=Z_{11}$となります。
アンテナで消費される電力に寄与するのは$Z_{11}$の抵抗分のみなので$P_0=R_{11}|I|^2$となります。
そのため、
\[M_0=\frac{|E_0|^2}{R_{11}|I|^2}\]
となります。
イには7.「$\frac{|E_0|^2}{R_{11}|I|^2}$」が入ります。
ウ
$Z_i$の抵抗分を$R_i$とすると$R_i=R_{11}+R_{12}$と表せます。
アンテナA,Bそれぞれに電流$I$を供給するので$P=2(R_{11}+R_{12})|I|^2$となります。
一方、点Oでの電界強度はアンテナA,Bは同じ位置にあるとみなすことができるので、$|E|=|2E_0|$です。
そのため、
\[
M=\frac{|2E_0|^2}{2(R_{11}+R_{12})|I|^2}
\]
となります。
ウには5.「$\frac{|2E_0|^2}{2(R_{11}+R_{12})|I|^2}$」が入ります。
エ
文の通り、$G$の式にこれまでの結果を代入すると
\[
G=M/M_0=\frac{2R_{11}}{R_{11}+R_{12}}
\]
そのため、エには8.「$\frac{2R_{11}}{R_{11}+R_{12}}$」が入ります。
オ
相互インピーダンスはアンテナ同士の結合度合いによって変わります。
この結合度合いはアンテナ間距離$d$で決まるので、$d$の大きさにより$G$を変えることができます。
そのため、オには9.「$d$」が入ります。
R.4.1 無線工学B（2回目） B-2
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B B-2
TEM波に関する穴埋め問題です。
ア
TEM波は磁界、電界成分が伝搬方向に垂直なモードの電波です。
そのため、伝搬方向にはこれらの成分を持ちません。
そのため、アには4.「持たない」が入ります。
イ
TEM波では電界成分と磁界成分は同相で振動します。
そのため、イには「同相」が入ります。
ウ
導波管では管軸方向と垂直に電界か磁界のどちらかの成分しかもつことができません。
そのため、TEM波は自遊空間などでは一般的なモードですが、導波管を伝搬することはできません。
ウには9.「できない」が入ります。
エ
真空の固有インピーダンスは$120\pi$です。
そのため、エには8.「$120\pi$」が入ります。
真空の誘電率(約$\frac{1}{36\pi}\times 10^{-9}$)と透磁率($4\pi \times 10^{-7}$)から求めることもできますが、覚えておいたほうが早いでしょう。
オ
TEM波では位相速度は光の速度と等しくなります。
そのため、オには1.「等しい」が入ります。
R.4.1 無線工学B（2回目） B-3
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B B-3
中波(MF)と短波(HF)の伝搬に関する正誤問題です。
ア
MFはD層で第1種減衰を受け、E層反射で伝搬します。
夜になるとD層が消滅し、E層反射で長距離を伝搬します。
そのため、アは正しいので答えは1です。
イ
地表波として伝搬する場合、水平偏波のほうが伝搬損が大きくなります。
これは水平偏波は大地と平行な電界成分を持つので、この電界成分により大地に電流が誘起されてその分が伝搬損となります。
イの文には垂直偏波のほうが伝搬損が大きいという記載なので誤りです。
そのため、答えは2です。
ウ
海上には山岳などの障害物がないため、海上のほうが陸上に比べて遠方まで伝搬します。
そのため、ウは誤りなので答えは2です。
エ
HFは電離層の臨界周波数などの影響を受けます。
時間により電離層の状況が変化し、周波数により反射する電離層の高さなどが変わるので、この文は正しいです。
そのため、エの答えは1です。
オ
電離層の異常現象はHFが伝搬する層で発生しやすいので、HFの方がこれらの減少に影響をうけやすいです。
そのため、オの文は正しいので、答えは1です。
R.4.1 無線工学B（2回目） B-4
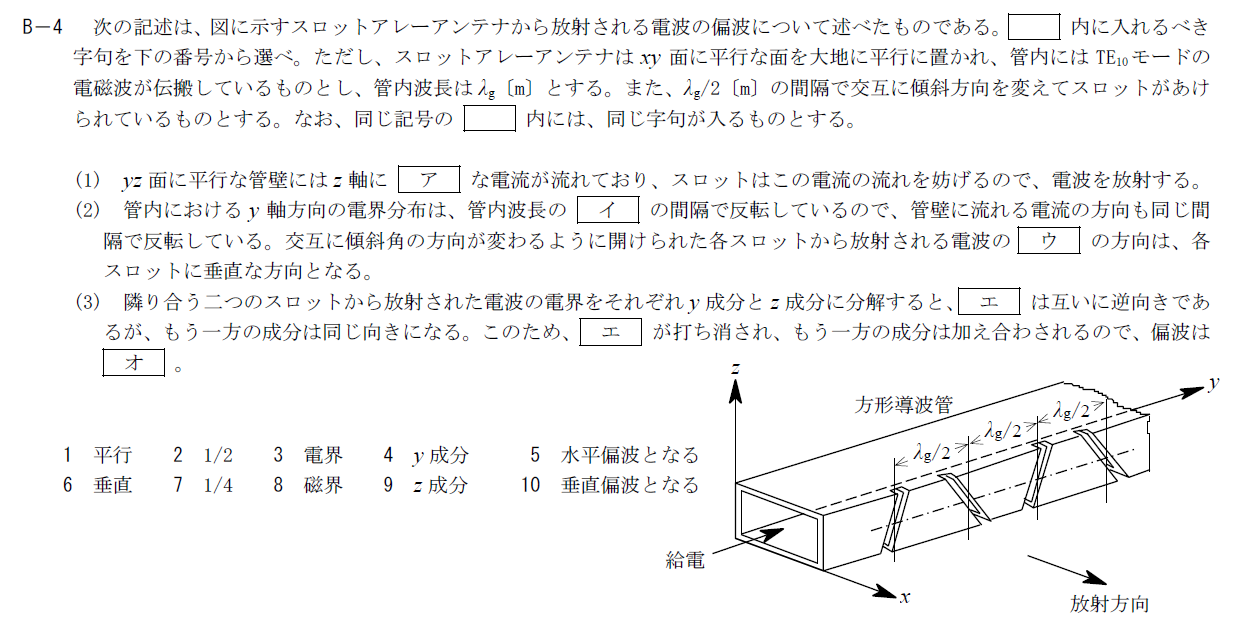
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B B-4
この問題の文章は令和3年7月(1回目)のA-12の問題と同じになっています。
空欄の位置は異なるので、気をつけましょう。
ア
$\rm{TE_{10}}$モードの伝搬なのでz軸方向に電界が分布します。
そのため、管壁にはz軸と平行な電流が流れます。
アには1.「平行」が入ります。
イ
一般に電波は1/2波長ごとに向きが反転します。
導波管内の電界分布は管内波長で決まりますが、分布は同じです。
そのため、イには2.「1/2」が入ります。
ウ
スロットはコンデンサのような働きをするので、電界の方向は各スロットに垂直となります。
そのため、ウには3.「電界」が入ります。
エ
図のように電界のz成分はスロットごとに逆向きになります。
そのため、エには9.「z成分」が入ります。
オ
電界のz成分はスロットごとで打ち消し合うので残る電界は管軸に平行なy成分のみです。
そのため、スロットアレーアンテナの偏波は水平偏波となり、オには5.「水平偏波」が入ります。
R.4.1 無線工学B（2回目） B-5
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学B B-5
この問題は令和3年1月の1回目のB-5と全く同じ問題です。
ここではもう少し詳しく解説します。
ア
問題の図1の三角形にピタゴラスの定理を適用すると
\[
L’=\sqrt{L^2+\left( \frac{D}{2}\right)^2}
\]
となります。
そのため、アには6.「$\sqrt{L^2+\left( \frac{D}{2}\right)^2}$」が入ります。
イ
$\Delta L$による位相差$\Delta \theta$は①の式を使って次のように表せます。
\[
\Delta \theta =\frac{2\pi}{\lambda}\Delta L=\frac{2\pi}{\lambda}\frac{D^2}{8L}=\frac{\pi D^2}{4\lambda L}
\]
そのため、イには2.「$\frac{\pi D^2}{4\lambda L}$」が入ります。
ウ
十分離れた点ではアンテナ中心とアンテナの縁からの電界強度は同じ大きさになります。
位相差がない時は単純にアンテナ中心と縁からの電界強度の和となります。
そのため、ウには8.「$2E_0$」が入ります。
エ
③の式の2つ目の等号の方を先に考えるとわかりやすいでしょう。
問題の図2を考えましょう。
$E_0’=E_0$なので、$E_0,E_0’$それぞれと$E’$のなす角は$\Delta \theta/2$となります。
そのため、
\[
E’=2E_0\cos \Delta \theta/2=E_0\sqrt{2(1+\cos \Delta \theta)}
\]
となります。
そのため、エには9.「$\sqrt{2}E_0\sqrt{(1+\cos \Delta \theta)}$」が入ります。
オ
$L=L_{\rm{min}}$の時、$\Delta \theta =\pi /8$なので、
\[
\frac{\pi D^2}{4\lambda L_{\rm{min}}}=\pi /8 \\
L_{\rm{min}}=\frac{2D^2}{\lambda}
\]
となります。。
そのため、オには10.「$\frac{2D^2}{\lambda}$」が入ります。
まとめ
令和4年1月2回目の1陸技の無線工学BのB-1~5を解いてみました。
1陸技は類似問題が多く出題される試験です。数値や空欄の位置を変えただけの問題もあります。
暗記だけでなく解き方もしっかり理解しておきましょう。
このサイトのコンテンツも充実させていきたいと思いますので参考にしていただければ幸いです。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人
コメント