R.4.1 無線工学B(1回目) A-1

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-1

【ゆっくり解説】第一級陸上無線技術士 R.4 1月 無線工学B(1回目)A-1
令和4年1月の1陸技の試験1回目の無線工学BのA-1の問題について解説します。ブログでも解説を記載しています。資格 #無線 #第一級陸上無線技術士

【資格】無線従事者のための物理学-電磁波の導出-
MathJax.Hub.Config({tex2jax: {inlineMath: , ]}});無線従事者をはじめとする技術関係の資格試験でいきなり覚えろと言わんばかりに公式などが出てきて困惑した経験はないでしょうか?私は理解しないと次に...
A,B
この問題ではAとBはセットです。 導出手順がわかっていればマクスウェル方程式の両辺に回転($\nabla \times$)を取ることがわかるでしょう。 もし、この手順を忘れていても問題文から推測できます。 ④の式を見てみましょう。 この式は \[ \nabla \times \nabla \times E =\nabla \nabla \cdot E -\nabla^2 E \] となります。 問題文から右辺はわかっています。 右辺はベクトル量になっているので左辺もベクトル量になっている必要があります。 もし、$\nabla \times E$に発散を取ると左辺がスカラー量になってしまうので、Bには$\nabla \times$が入っている必要があります。 以上からAには「回転」、Bには「$\nabla \times$」が入ります。C,D
CとDもセットになっています。 ③の式に②と④と⑤を代入してみましょう。 \[ (左辺)=-\nabla ^2 E \\ (右辺)=-j\omega \mu (\sigma +j\omega \epsilon)E \] となるので、 \[ \nabla ^2 E -j\omega \mu (\sigma +j\omega \epsilon)E =0 \] です。 (5)の式と比較すると$\gamma^2 =-j\omega \mu (\sigma +j\omega \epsilon)$となります。 そのため、Cには$\nabla^2$、Dには$-j\omega \mu (\sigma +j\omega \epsilon)$が入ります。 以上から答えは2です。R.4.1 無線工学B(1回目) A-2

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-2
YouTube
作成した動画を友だち、家族、世界中の人たちと共有
A
受信点は原点Oから十分離れたところにあるので、アンテナaとアンテナbは同じ距離と近似できます。 aとbの位相差分だけ電界強度に差が出ます。 $E_1$と$E_2$の式を見比べると違いはKM倍です。 Mは電流がM倍になったことを表すのでKは位相差を表す係数と考えるのが自然でしょう。 入力は同位相なので、アンテナa,b間の位相差は伝搬経路による位相差のみです。 2つのアンテナの経路差は図から$l\cos \theta$と計算できるので$K=e^{j\beta l \cos \theta}$となります。 そのため、Aには$e^{j\beta l \cos \theta}$が入ります。B
$E_1$と$E_2$を足せば \[ E=A\frac{e^{-j\beta d}}{d}D(1+KM) \] となるので、Bには$1+KM$が入ります。C
アンテナa,bとして、無指向性点放射源を使用する場合、$E_1,E_2$のDが1になるので、 \[ E=A\frac{e^{-j\beta d}}{d}(1+KM) \] となります。 つまり、$1+KM$は無指向性点放射源の配列に指向性係数と言えます。 指向性Dのアンテナの配列の合成指向性はBまでの結果から$D(1+KM)$なので、アンテナ素子の指向性と無指向性点放射源の指向性の積がアンテナ配列の指向性となっています。 そのため、Cには「無指向性点放射源」が入ります。 以上から答えは2です。R.4.1 無線工学B(1回目) A-3

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-3
R.4.1 無線工学B(1回目) A-4
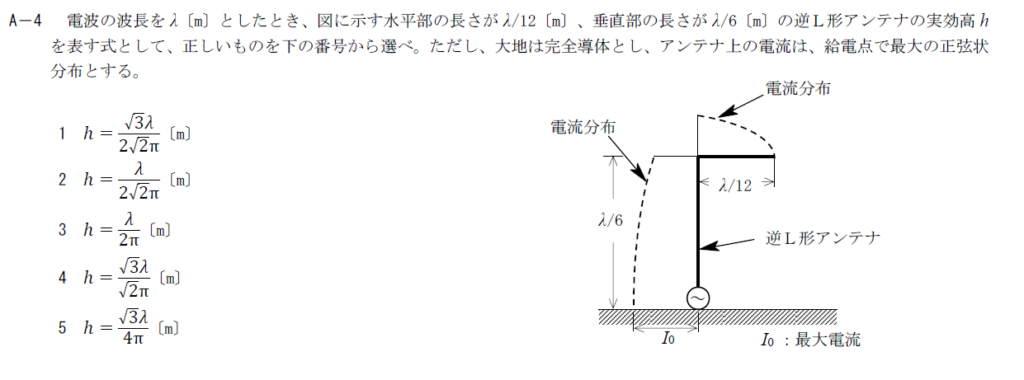
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-4
YouTube
作成した動画を友だち、家族、世界中の人たちと共有
R.4.1 無線工学B(1回目) A-5
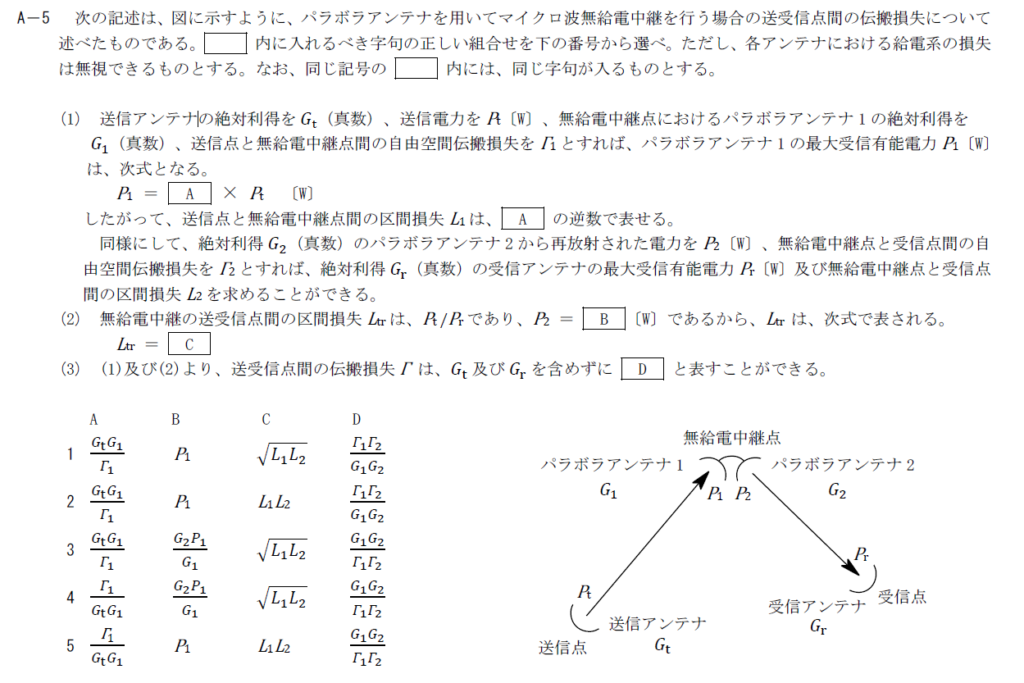
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学B A-5
A
まず、送信点から中継点までの伝搬を考えます。 フリスの公式から$P_1=\frac{G_tG_1}{\Gamma_1}P_t$となります。 そのため、Aには$\frac{G_tG_1}{\Gamma_1}$が入ります。B
問題文から給電系の損失は無視できるので、$P_2=P_1$となります。 そのため、Bには$P_1$が入ります。C
$P_r$もAと同様に考えて \[ P_r=\frac{G_2G_r}{\Gamma_2}P_2 \\ =\frac{G_2G_r}{\Gamma_2}\frac{G_tG_1}{\Gamma_1}P_t \] となります。 空間損失は$P_t/P_r=\frac{\Gamma_1}{G_tG_1}\frac{\Gamma_2}{G_2G_r}=L_1L_2$です。 そのため、Cには$L_1L_2$が入ります。D
送受信点間の損失を$\Gamma$でまとめると$P_r=\frac{G_tG_r}{\Gamma}P_t$と表せるので、$\Gamma =\frac{\Gamma_1\Gamma_2}{G_1G_2}$となります。 そのため、Dは$\frac{\Gamma_1\Gamma_2}{G_1G_2}$です。 以上から答えは2です。まとめ
今回は先日行われた令和4年1月1回目の1陸技の無線工学BのA-1~5を解いてみました。 先週受験した方はお疲れさまでした。 試験はいかがだったでしょうか? まだ結果は発表されていませんが、回答は発表されているので自己採点してみるのもいいでしょう。 勉強法 第一級陸上無線技術士の勉強法とおすすめ参考書参考文献
リンク
リンク
上の難易度が高い人
リンク
リンク

コメント