令和5年7月の1陸技の試験1回目の無線工学AのA-1~5の問題について解説します。
R.5.7 無線工学A(1回目) A-1

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学A A-1
IEEE802.11無線LANのCSMA/CAに関して誤った選択肢を選ぶ問題です
誤った選択肢は5です。
前半の隠れ端末問題に関して言及している「~~可能性があるため、」までの記述は正しいです。
後半の「データ送信の許可をAPに求める」が間違っています。 RTS/CTSでは端末からRTSをAPに対し送信し、それを受信したAPが全体に対してCTSを送信します。 CTSにより他の端末は無線チャネルがビジーであることが分かるため、隠れ端末同士のデータ衝突が防がれます。
そのため、答えは5です。
R.5.7 無線工学A(1回目) A-2

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学A A-2
地上系デジタル放送に関する標準方式のガードインターバルに関する問題です。
A,B
AとBの空欄はガードインターバルに関する内容です。
ガードインターバルは有効シンボルの後半部分をシンボルの前に付加して、マルチパス等による影響を低減する手法です。
この内容からAには「後」、Bには「前」が入ります。
C
$A\rightarrow C$の経路と$A\rightarrow B\rightarrow C$の2つの経路の伝搬時間は次の通りです。
$A\rightarrow C$
\[ \frac{25\times 10^3}{3\times 10^8}=\frac{25}{3}\times 10^{-5} \rm{[s]} \]
$A\rightarrow B\rightarrow C$
\[ \frac{(40+25)\times 10^3}{3\times 10^8}=\frac{65}{3}\times 10^{-5} \rm{[s]} \]
これらの差が遅延時間差となるのでCには \[ \frac{40}{3}\times 10^{-5} \rm{[s]}=133 \times 10^{-6}\rm{[s]}=133\rm{[\mu s]} \] が入ります。
D
有効シンボル長$1.008\rm{ms}=1008\rm{\mu s}$に対して、ガードインターバル比が$1/8$なのでガードインターバルは \[ \frac{1008}{8}=126\rm{[\mu s]} \] となります。
遅延時間差と比べてガードインターバルの方が短いので(2)の④の記述の条件を満たさないのでシンボル間干渉が多きいと言えます。
そのため、Dには「大きい」が入ります。
以上から答えは3です。
R.5.7 無線工学A(1回目) A-3

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学A A-3
スーパーヘテロダイン受信機のスプリアスレスポンスに関する問題です。
この問題は全く同じ問題が令和4年7月1回目A-7で出題されています。
下記の記事をご参照ください。

空欄は下記のとおりです。
- A:$(f_0/2)\pm f_{IF}$
- B:$2f_0\pm f_{IF}$
- C:$f_0\pm (f_{IF}/2)$
以上から答えは1です。
R.5.7 無線工学A(1回目) A-4
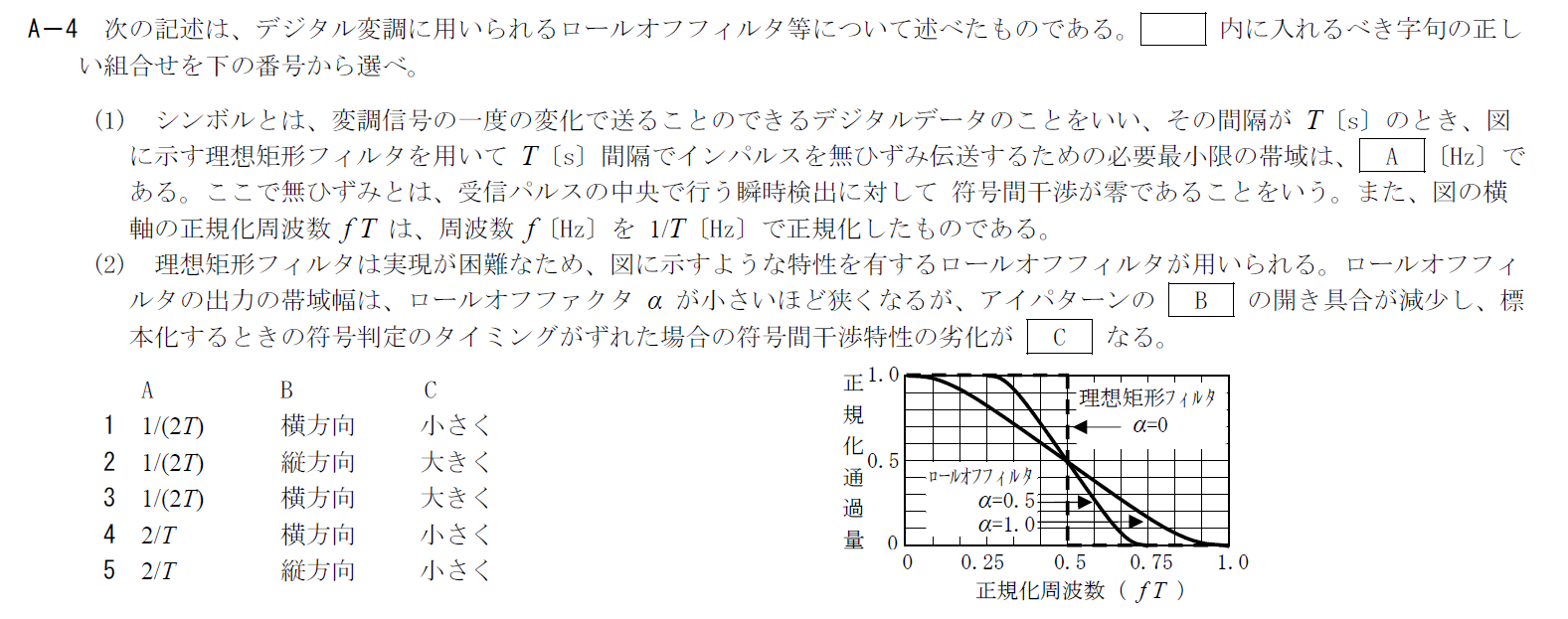
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学A A-4
デジタル変調のロールオフフィルタに関する問題です。
この問題は同様の問題が令和4年1月1回目B-5で出題されています。 問題文がほぼ同じで一部が異なります。
下記の記事もご参照ください。

また、ロールオフフィルタに関する類似問題が令和5年1月1回目B-5で出題されています。 こちらの問題も合わせて押さえておくとよいでしょう。

A
この空欄は令和4年1月1回目B-5のイの空欄と同じです。
理想矩形フィルタを使用する場合、fT=0.5の時に通過量が1から0に切り替わるので、f=1/(2T)の時が無ひずみ伝送するための最小限の帯域となります。 ここで言う無ひずみは符号間で干渉しない(符号間干渉が零)という意味です。
そのためAには$1/(2T)$が入ります。
B,C
Bの空欄を含む部分は令和4年1月1回目B-5の文章に新しく追加されています。Cはオの空欄と同じです。
ロールオフファクタが小さいほど$\alpha =0$の理想矩形フィルタに近づきます。 これによりフィルタは狭帯域になります。この時、時間軸方向では単位時間当たりの送信パルス数が増えます。 アイパターンの横軸は信号の時間軸方向の変化を表すので、パルス数が増える分アイパターンは横方向の開き具合が減少します。 アイパターンの縦軸は振幅を表します。
いずれも開き具合が小さいほど情報の区別が難しくなり正確な情報伝送が難しくなります。
ロールオフファクタを小さくすると符号間干渉特性が劣化することを意味します。
上記の内容からBには「横方向」、Cには「大きく」が入ります。
以上から答えは3です。
R.5.7 無線工学A(1回目) A-5

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学A A-5
位相変調の最大周波数帯域幅を計算する問題です。
値が違う同じ問題が令和3年7月2回目A-3で出題されています。
下記の記事もご参照ください。

$F_d$は変調信号の周波数$f_m$、位相変調指数を$m_p$とすると \[ F_d=m_pf_m \] となります。
問題文の値を代入すると \[ F_d=1.2 \times 0.5 \times 50 \times 10^3 =30 \times 10^3\rm{[Hz]} \] です。 最大の周波数帯域幅を求めるので変調指数が最大にずれた時の値を使うため$1.2$をかけています。
与えられた$B_w$の式を代入すると \[ B_w=2(f_m+F_d)=160 \times 10^3\rm{[Hz]}=160\rm{[kHz]} \] となります。
以上から答えは2です。
まとめ
今回は令和5年7月の無線工学A(1回目)の試験A-1~A-5の問題について解説しました。 無線LANに関する問題など過去問であまり出題されていないタイプの問題も出題されています。 過去問だけでは対策しずらいので最悪捨てて他の問題に集中することも考慮に入れましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント