令和4年1月の1陸技の試験、無線工学AのB-1～5の問題について解説します。
R.4.1 無線工学A（1回目） B-1
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学A B-1
衛星通信の多元接続方式に関する問題です。
ア
(1)は時分割多元接続(TDMA)方式に関する記述です。
TDMAでは各局の送信タイミングをずらすことで多元接続を実現しています。
そのため、アには1.「送信タイミング」が入ります。
イ
(2)は周波数分割多元接続(FDMA)方式に関する記述です。
FDMAでは各地球局に異なる周波数を割り当てて多元接続を実現しています。
この時、各チャネルの間にはガードバンドを設けてチャネル間干渉を防いでいます。
そのため、イには6.「ガードバンド」が入ります。
ウ
(3)は符号分割多元接続(CDMA)方式に関する記述です。
CDMAでは送受信で同じ符号列で変調し、相関を取ることで必要な信号のみを取り出します。
そのため、ウには9.「同じ」が入ります。
エ、オ
(4)はSCPC方式に関する記述です。
SCPCはSingle Chennel Per Carrierの略で、一つのチャネルに対して一つの搬送波を割り当てます。
中継器の帯域内に異なる周波数の搬送波を並べることでFDMA方式と同様のことができます。
以上から、エには3.「1つ」、オには10.「周波数分割多元接続(FDMA)方式の」が入ります。
R.4.1 無線工学A（1回目） B-2
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学A B-2
アナログのスペクトルアナライザの原理に関する問題です。
ア
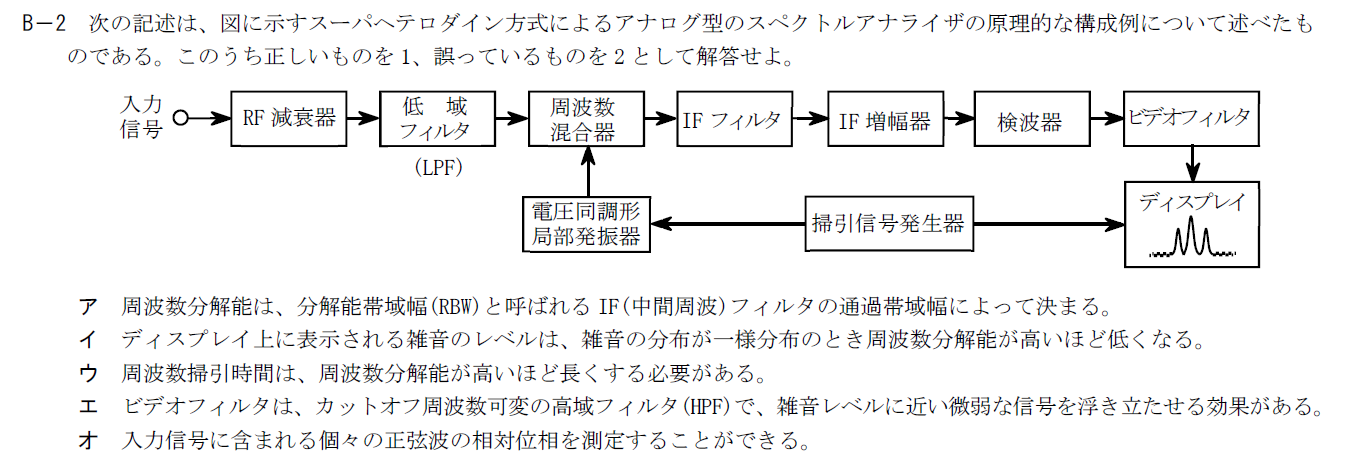
アは正しい記述で答えは1です。
スペクトルアナライザの分解能はIFフィルタの帯域幅で決まり、この帯域幅を分解能帯域幅(RBW:Resolution Band Width)と呼びます。
帯域幅が狭いほど周波数分解能が高くなり、その分、掃引時間が長くなります。
イ
イは正しい記述で答えは1です。
雑音の分布が一様な時は熱雑音が見えていると考えて良いです。
熱雑音の大きさは周波数帯域幅に比例し、帯域幅が狭いほど小さくなります。
一方、アに記載したとおり、RBWが狭いほど周波数分解能が高くなります。
そのため、「周波数分解能が高い」＝「RBWが狭い」＝「（熱）雑音が小さい」となります。
ウ
ウは正しい記述で答えは1です。
アで記載したとおり、周波数分解能が高いほど周波数掃引時間が長くなります。
エ
エは誤った記述で答えは2です。
ビデオフィルタは高域フィルタではなく低域フィルタです。
雑音や急激な変動はビデオフィルタで低減されるので、雑音に近い微弱な信号を浮き立たせる効果はあります。
そのため、後半は正しい記述です。
オ
オは誤った記述で答えは2です。
アナログ式のスペクトルアナライザでは周波数を掃引してIFフィルタを通った電力をディスプレイに表示するので、ここの正弦波の相対位相を測定することはできません。
R.4.1 無線工学A（1回目） B-3
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学A B-3
受信機の雑音指数の測定に関する問題です。
ア
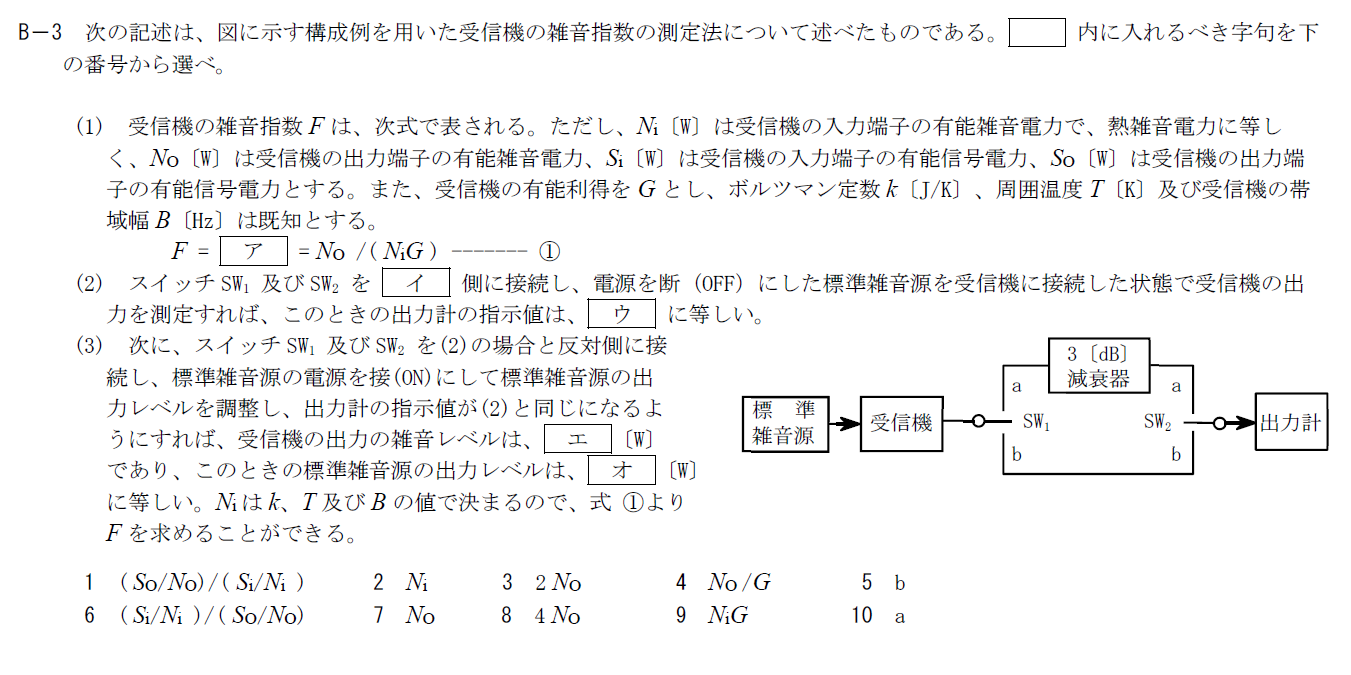
雑音指数は増幅器や伝送路の内部雑音でどれくらいS/Nが悪くなるか示す指標です。
雑音指数の定義は次のようになっています。
\[
F=\frac{(S_i/N_i)}{(S_o/N_o)}=\frac{S_i}{S_o}\frac{N_o}{N_i}=\frac{N_o}{N_iG}
\]
ここで$G=S_o/S_i$です。
以上からアには6.「$(S_iN_i)/(S_o/N_o)$」が入ります。
イ、ウ
(2)では受信機単体の有能雑音電力を測定します。
受信機の出力をそのまま測定したいのでスイッチをb側に倒し、出力計で直接$N_o$測定します。
そのため、イには5.「b」、ウには7.「$N_o$」が入ります。
エ
減衰器で3dB下がる（電力が1/2倍になる）ので、受信機出力の雑音レベルは$2N_o$となります。
そのため、エには2.「$2N_o$」が入ります。
オ
エの結果から$GN_i+N_o=2N_o$なので、$N_i=N_o/G$となります。
そのため、オには4.「$N_o/G$」が入ります。
R.4.1 無線工学A（1回目） B-4
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学A B-4
QPSK復調器に関する問題です。
ア、イ
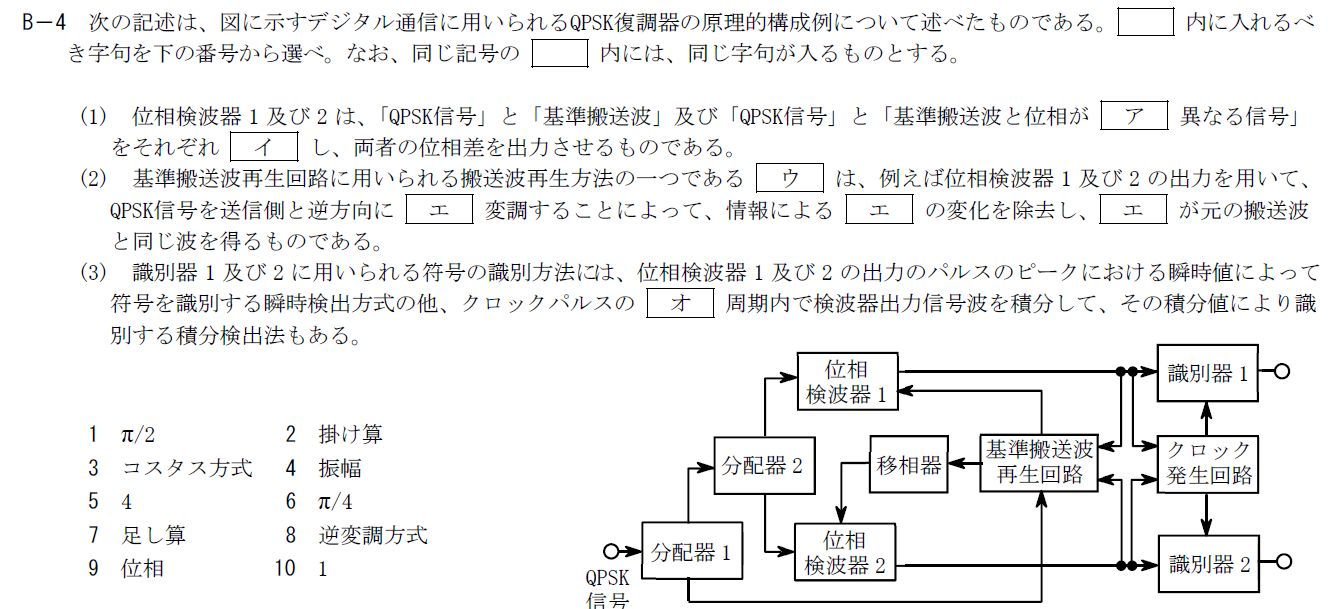
2つの位相検波器ではQPSK信号に対してそれぞれ「基準搬送波」と「基準搬送波と位相が$\pi/2$だけ異なる信号」を掛け算します。
その結果をローパスフィルターに通して低周波成分のみ取り出すことで変調信号を得ることができます。
QPSK信号を$A\cos (\omega t +\phi_i)$、基準搬送波を$A\cos (\omega t +\frac{\pi}{4})$とすると、次のようになります。
ただし、$\phi_i=0,\pi/2,\pi, 3\pi/2$です。
\[
A\cos (\omega t +\phi_i)A\cos (\omega t +\frac{\pi}{4}) \\
=\frac{\pi}{2}\left\{\cos (2\omega t +\phi_i+\frac{\pi}{4})+\cos (\phi_i-\frac{\pi}{4})\right\}
\]
ローパスフィルタを通すと$\frac{A^2}{2}\cos (\phi_i-\frac{\pi}{4})$となります。
基準搬送波から位相を$\pi/2$ずらした信号をかけたときも同様に$\frac{A^2}{2}\sin (\phi_i-\frac{\pi}{4})$となります。
2つの位相検波器の出力から位相$\phi_i$を決めることができます。
以上にはアには1.「$\pi/2$」、イには2.「掛け算」が入ります。
ウ、エ
(2)は基準搬送波再生回路の原理に関する記述です。
ウはすぐにはわからないと思うのでエから考えるのが良いでしょう。
基準搬送波再生回路は元の搬送波を得ることが目的なので、変調信号の情報をQPSK信号から除去する必要があります。
QPSKは位相変調の一種なので、検波器の出力を使って送信側と逆に位相変調すれば元の搬送波が得られることになります。
この方式は逆に変調するので逆変調方式と呼ばれています。
以上からウには、8.「逆変調」、エには9.「位相」が入ります。
オ
位相検波器の出力は2値しか取らないのでクロックパルス1周期分を積分することで、符号を識別することもできます。
4周期も積分してしまったら4周期分の平均値になるので符号の識別はできません。
そのため、オには10.「1」が入ります。
R.4.1 無線工学A（1回目） B-5
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月1回目 無線工学A B-5
デジタル変調のロールオフフィルタに関する問題です。
ア
アは用語の定義です。
シンボルとは変調信号の一度の変化で送ることができるデジタルデータのことです。
そのため、アには7.「変調信号」が入ります。
イ、ウ
理想矩形フィルタを使用する場合、fT=0.5の時に通過量が1から0に切り替わるので、f=1/(2T)の時が無ひずみ伝送するための最小限の帯域となります。
ここで言う無ひずみは符号間で干渉しない（符号間干渉が零）という意味です。
そのため、イには3.「1/(2T)」、ウには10.「符号間干渉」が入ります。
エ
フィルタのインパルス応答がシンボル間隔Tの整数倍で零となれば符号間干渉を零にできます。
そのため、エには10.「零」が入ります。
オ
ロールオフファクタが小さいほど理想矩形フィルタに近い特性になるため、出力の帯域幅は狭くなりますが、その分符号判定のタイミングがシビアになるため、符号間干渉特性の劣化は大きくなります。
そのため、オには9.「大きく」が入ります。
まとめ
今回は先月行われた令和4年1月1回目の1陸技の無線工学AのB-1~5を解いてみました。
無線工学の最後の5問は小問集合のような形式になっています。
誘導がしっかりしていて解きやすい問題も多いですが、最初に間違えるとすべてが間違うリスクもあります。
問題文をしっかり読みながら落ち着いて解きましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人
コメント