令和5年1月の1陸技の試験1回目の無線工学AのA-6~10の問題について解説します。
R.5.1 無線工学A(1回目) B-1

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学A B-1
理論的な伝送容量の限界(シャノンの限界)に関する問題です。
ア
シンボル長$T$の間に$n$bit分の情報が伝送され、1bitあたりのエネルギーが$E_b$なので、$T$の期間のエネルギーは \[ nE_b \] です。
そのため、アには4.「$nE_b$」が入ります。
イ
$1$[Hz]あたりの雑音電力密度が$N_0$なので、これに帯域幅$B$をかければ雑音電力$N$になります。
そのため、イには1.「$N_0B$」が入ります。
ウ
$T$[s]あたりのエネルギーが$nE_b$なので、 \[ C=nE_b/T \] となります。
そのため、ウには7.「$nE_b/T$」が入ります。
エ
イとウの結果から \[ C/N=nE_b/TN_0B=E_bR/N_0B \] となります。
そのため、エには8.「$E_bR/N_0B$」が入ります。
オ
$R/B=a$とおいて、$E_b/N_0$を$a$で表して$a\rightarrow 0$の極限をとることにします。
③の式から \[ a=\log_2\{1+aE_b/N_0\} \\ 2^a=1+aE_b/N_0 \\ E_b/N_0=\frac{2^a-1}{a} \] となります。 ロピタルの定理を使って極限をとると \[ E_b/N_0 =\ln 2 \] です。
この結果をデシベルに直すと \[ E_b/N_0=-1.6\rm{[dB]} \] となります。
以上からオには10.「$-1.6$」となります。
R.5.1 無線工学A(1回目) B-2

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学A B-2
FFTアナライザに関する問題です。
この問題は令和3年7月1回目B-2で類似問題が出題されています。
下記の記事をご参照ください。

ア
FFTアナライザはフーリエ変換により信号処理を行うので、周波数ごとの振幅と位相の情報を得ることができます。
上記の内容からアの記述は正しいので答えは1です。
イ
D-A変換ではなくA-D変換してからFFTする装置なので、この記述は誤りです。
そのため、イは誤りで2です。
ウ
FFTアナライザは時系列の入力信号を演算するので限られた時間内の信号も解析できます。
そのため、ウは正しい記述なので答えは1です。
エ
FFTアナライザは被測定信号をフーリエ変換して測定するので、元の被測定信号を再生するには逆フーリエ変換をすればいいことになります。
そのため、エは正しい記述なので答えは1です。
オ
エイリアシングによる誤差をなくすには標本化周波数を入力信号の2倍以上にする必要があります。
そのため、この記述は後半が誤りなので答えは2です。
R.5.1 無線工学A(1回目) B-3

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学A B-3
WiMAXの空中線電力偏差の測定に関する問題です。
この問題は令和3年7月2回目B-3で全く同じ問題が出題されています。
下記の記事をご参照ください。

答えは
- ア:6.「最も長い時間」
- イ:7.「最大出力と」
- ウ:8.「平均」
- エ:10.「$T/B$」
- オ:4.「大きい」
R.5.1 無線工学A(1回目) B-4

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学A B-4
AMの検波の原理に関する問題です。
この問題は令和3年7月2回目B-4で全く同じ問題が出題されています。
下記の記事をご参照ください。

答えは
- ア:1.「包絡線」
- イ:7.「$\frac{1}{2}E_0(t)\left[\cos\left\{\theta_s-\phi_0(t)\right\}+\cos\left\{2\omega_ct +\theta_s +\phi_0(t)\right\}\right]$」
- ウ:5.「高周波成分」
- エ:8.「$\theta_s-\phi_0(t)$」
- オ:9.「$E_0(t)\cos \theta _s$」
R.5.1 無線工学A(1回目) B-5
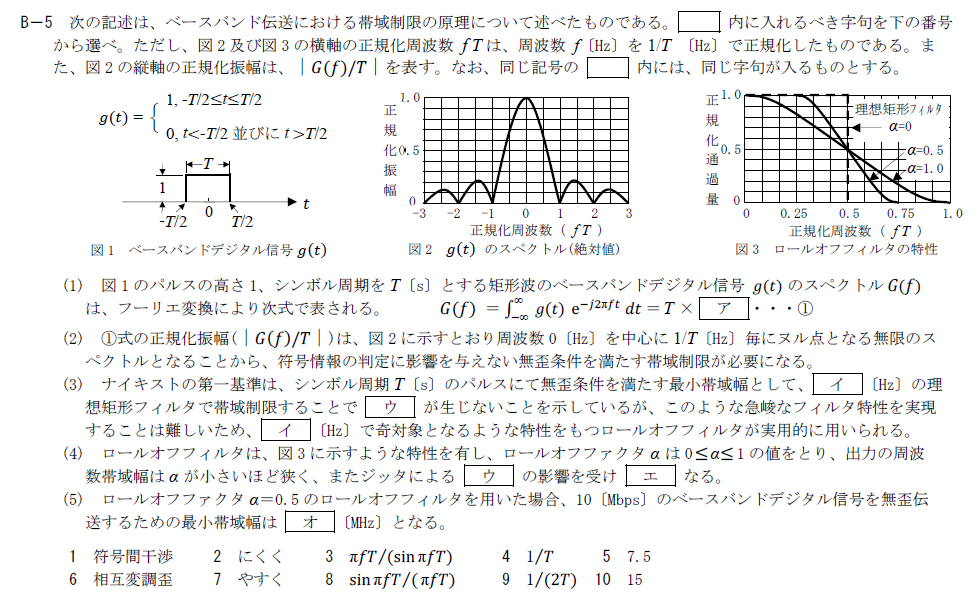
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学A B-5
ベースバンド伝送における帯域制限に関する問題です。
ア
(1)ではパルス波形をフーリエ変換しています。
計算自体はそれほど難しくないので実際に計算してみましょう。 \[ G(f)=\int^{T/2}_{-T/2}e^{-j2\pi ft}dt \\ =\left[ \frac{1}{-j2\pi f}e^{-j2\pi ft}\right]^{T/2}_{-T/2} \\ =j\frac{e^{-j2\pi fT/2}-e^{j2\pi fT/2}}{2\pi f} \\ =T\times \frac{\sin \pi fT}{\pi fT} \]
そのため、アは8.「$\frac{\sin \pi fT}{\pi fT}$」です。
イ、ウ
理想矩形フィルタでは$fT=1/2$で正規化通過量が1から0に切り替わるので、$f=1/(2T)$で帯域制限することにより符号同士が干渉することなく歪をなくすことができます。
この符号同士の干渉を符号間干渉といいます。
そのため、イには9.「$1/(2T)$」、ウには1.「符号間干渉」が入ります。
エ
図3から推測できる通りロールオフファクタが0に近いほど理想矩形フィルタに近づくことになります。
理想矩形フィルタに近づくほど出力の帯域幅が狭くなりますが、その分符号判定のタイミングがシビアになります。 そのため、信号の時間的なズレやゆらぎであるジッタの影響を受けやすくなります。
このことからエには7.「やすく」が入ります。
オ
$\alpha =0.5$の正規化通過量がゼロになるのは$fT=0.75$の時です。 問題文から$1/T=10\rm{[MHz]}$なので、$f=7.5\rm{[MHz]}$となります。
そのため、オには5.「7.5」が入ります。
まとめ
今回は令和5年1月の無線工学A(1回目)の試験B-1~B-5の問題について解説しました。 B問題は特に過去問と同じ問題が出やすい傾向があります。 同じ年の同じ設問の問題が出題されることもあるくらいなので、過去問演習がより重要です。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント