無線従事者試験は受験資格が設定されていないという性質上、いろいろな人が受験するため、無線工学の科目で出てくる数学に苦労した人も多いのではなだろうか。
前回、数学の基礎的な内容として、数の分類に始まりよく使う初等関数について紹介した。
今回は微分方程式を扱う。今回からは無線従事者試験の問題を解く上ではパターンに当てはめれば解けるがそのパターンがなぜそうなっているのか考えるための基礎的な内容を扱っていく。ベクトル解析については別途まとめていきたい
この記事を読むことによって次のことが分かります。
- RLC回路での微分方程式
- 振動を表す式
微積分って何?
まず、微積分って何という状態の人も多いと思うので簡単に触れておく。今回はこれらを道具として使うので定義などは割愛したい。
とりあえずwikipediaへのリンクをはっておく。
微分: https://ja.wikipedia.org/wiki/%E5%BE%AE%E5%88%86
積分: https://ja.wikipedia.org/wiki/%E7%A9%8D%E5%88%86%E6%B3%95
ざっくりいうと
- 微分は変化量
- 積分はグラフが囲む範囲の面積
を表す。積分と微分はそれぞれ逆演算の関係にあって関数\(f(x)\)の積分を微分した結果は\(f(x)\)になる。
よく使うシチュエーション
- 微分:物理量の時間や空間での変化のしかたや勾配(電荷の変化量を計算して電流を求める、電位の勾配を計算して電界を求める等)
- 積分:物理量をこまかい区間で区切って足し上げる(電界の仕事を少しずつ足し上げて電位を求める等)
よく使う関数の微分
$ \frac{d}{dx}x^n=nx^{n-1}\\\frac{d}{dx}x^n=nx^{n-1} \\ \frac{d}{dx}x^n=nx^{n-1}\\ \frac{d}{dx}1=\frac{d}{dx}x^0=0 \\ \frac{d}{dx}e^x=e^x \\\frac{d}{dx}\log_e x=\frac{1}{x} \\ \frac{d}{dx}\sin x= \cos x \\ \frac{d}{dx}\cos x=-\sin x $
また、合成関数の微分もよく使うので押さえておきたい。
これは\(f(u(x))\)のように、\(f(x)\)が\(x\)の関数\(u(x)\)で書けるとき便利である。\(f\)を\(u\)の関数して\(u\)で微分し、改めて\(u\)を\(x\)で微分したものをかける。
\[ \frac{d}{dx}f(u(x))=\frac{df}{du}\frac{du}{dx}\]
具体的には次のような例がある。
$ \frac{d}{dx}\sin kx=k\cos kx \\\frac{d}{dx}e^{jkx}=jk e^{jkx} $
積分は上記のような結果となるように計算すればよい。
特に重要な性質は
- (e^x)は微分しなくても変化しないこと
- 三角関数は2回微分すると符号が反転して元に戻ること
である。
RLC回路と微分方程式
微分方程式とは関数の微分が含まれた方程式で、解としてその微分された関数を求めるものである。
回路でもかなりの頻度で使われるので具体例を交えてみていこう。
準備
まず下準備抵抗\(R\)、コイル\(L\)、コンデンサ\(C\)の両端の電圧を式で表しておく。
両端の電圧を\(E(t)\)、流れる電流を\(I(t)\)とする。
抵抗はオームの法則から$$E=RI$$、コイルはファラデーの電磁誘導の法則から$$E=-L\frac{dI}{dt}$$、コンデンサは\(E=\frac{Q}{C}\)が成り立ち、電流は単位時間当たりの\(Q\)の変化量なので$$E=\frac{1}{C}\int Idt$$が成り立つ。
LC回路と振動解
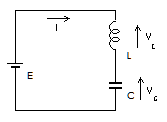
図から$$E=L\frac{dI}{dt}+\frac{1}{C}\int Idt$$が成り立つ。t=0でスイッチを入れて電流を流し始めたとする。
今回は直流電源をつないだ状態を考える。
両辺\(t\)で微分して$$\frac{d^2I}{dt^2}=-\frac{1}{LC}I$$となる。
ここで三角関数の2回微分すると符号が変わって元に戻るという性質が活きてくる。
\(\sin \)と\(\cos \)の両方が同じ性質を持つので一般解はこれらに係数をつけて足せばよい。この係数は初期条件によってきまる。$$I(t)=A\sin \omega t +B\cos \omega t$$
ここで\(\omega=\frac{1}{\sqrt{LC}} \)である。
\(A, B\)を決める。
\(t=0\)の時、コイルによって電流が流れないので\(I(0)=0\)、コンデンサに電荷はたまっておらずコンデンサの極板間の電圧は0だから\(E=-L\frac{dI}{dt}(0)\)となる。
計算すると$$A=E\sqrt{\frac{C}{L}}, B=0$$となる。
また、\(e^{jkx}\)のような指数関数の方に虚数が入っているときも同様のことが言える。オイラーの式\(e^{jx}=\cos x +j\sin x\)なので、複素数の範囲で係数を決め直すことと同じである。
以上から\(I(t)=E\sqrt{\frac{C}{L}}\sin \omega t\)となる。
三角関数は一定周期で同じ値を繰り返すので振動や波動を表す式であるので、LC直列回路では電流が振動することになる。
波動方程式
波動関数は2階の偏微分方程式で表される。
偏微分は多変数の関数を今注目している変数以外を固定して微分するものだと思ってもらえればよい。
無線従事者を受ける分には一切使わないが電磁波を表す式が出てきたときに波動方程式で解が波動を表すことを理解しておいてもらえればいいので、式の形を紹介して実際に正弦波を代入して成り立つことを見ていく。
波動方程式は$$\frac{\partial^2 u(x,t)}{\partial t^2}=v^2\frac{\partial^2 u(x,t)}{\partial x^2}$$で表せる。\(v\)は波の速度で波長\(\lambda\)、周波数\(f\)を用いて\(v=f\lambda\)ある。
3次元空間では右辺に\(y, z\)成分を足せばよい。
\(u(x,t)=\sin(kx-\omega t)\)を代入する。時間の項が負符号になっているのは慣例である。\(k=\frac{2\pi}{\lambda},\omega=2\pi f\)で、それぞれ波数と角周波数を表す。
波動方程式に代入してみる
$$(左辺)=\frac{\partial^2 }{\partial t^2}\sin (kx-\omega t)=-\omega ^2 \sin (kx-\omega t)=- (2\pi f)^2 \sin (kx-\omega t)$$
$$(右辺)=v^2\frac{\partial^2 }{\partial x^2}\sin (kx-\omega t)=-kv^2 \sin (kx-\omega t) =(2\pi f)^2 \sin (kx-\omega t)$$
となり、\(\sin (kx-\omega t)\)は波動方程式の解である。
まとめ
今回は微分積分とは何か紹介し、LC回路を実際に解いて電流が振動することを見た。
また波動方程式に実際に正弦波を代入し回なることを確認した。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人
次回予告
ベクトル解析か最近発散し始めたので一度無線工学の出題範囲を俯瞰しようと思う。
前回
次回
近日中
本シリーズについて
勉強法


コメント