令和3年7月の1陸技の試験、無線工学BのA-6~10の問題について解説します。
R.3.7 無線工学B(1回目) A-6

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B A-6
平行二線式給電線の静電容量を計算させる問題です。
平行二線式給電線の特性インピーダンス$Z_0$は線間隔$D=2\times 10^{-1}$[m]、直径$d=4\times 10^{-3}$[m]として次のように計算できます。 \[ Z_0 = 276\log \frac{2D}{d}=276 \times 2=552 \]
開放された終端から見たインピーダンス$Z$は次のように表せます。 \[ Z=\frac{Z_0}{j\tan(\frac{2\pi}{\lambda}l)} \] 題意から$\lambda=10, l=1.25$なので$\frac{2\pi}{\lambda}l=\pi/4$なので \[ Z=-jZ_0 \] となります。
これが等価なコンデンサのインピーダンスと等しいので$\frac{1}{j\omega C}=-jZ_0$となります。 Cについて解くと \[ C=\frac{1}{\omega Z_0}=\frac{1}{552\times 2 \pi \times 30 \times 10^6}=10\times 10^{-12} \] となります。 そのため、答えは1の10[pF]です。
途中$3\pi=9.4 \simeq 10$とすると計算が楽でしょう。 この問題もそうですが、1陸技の試験問題の答えの選択肢の差が離れているので、これくらいざっくり近似しても答えを絞れます。
R.3.7 無線工学B(1回目) A-7

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B A-7
定義どおりに計算しましょう。
反射係数
特性インピーダンスを$Z_0$、負荷インピーダンスを$Z_r$として、 \[ \Gamma =\frac{Z_r -Z_0}{Z_r+Z_0}=\frac{1}{5}(-1+j3) \] となります。
電圧定在波比$S_V$は \[ S_V=\frac{1+|\Gamma|}{1-|\Gamma|}=\frac{5+\sqrt{10}}{5-\sqrt{10}} \] となります。
以上から答えは4です。
R.3.7 無線工学B(1回目) A-8
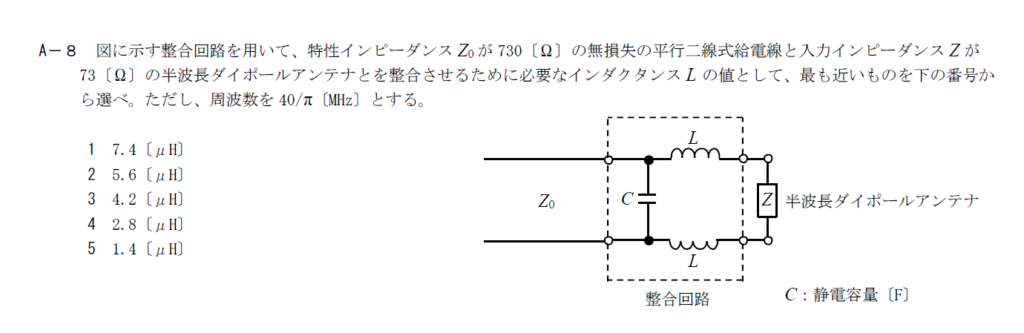
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B A-8
参考書等にはほとんどの場合、暗記するような書き方になっています。 暗記してもいいですが、ここでは与えられた回路図から計算します。
給電線から見た整合回路と半波長ダイポールアンテナの合成インピーダンスが給電線のインピーダンスが一致していればいいことになります。 コンデンサ1個とコイルと半波長ダイポールアンテナの直列回路と並列に接続されているので次の式が成り立ちます。 \[ \frac{1}{Z+j2\omega L}+j\omega C=\frac{1}{Z_0} \] 両辺に$Z+j2\omega L$をかけて、実部と虚部に分けると次のようになります。 \[ (1-2\omega^2 LC)+j\omega C=\frac{Z}{Z_0}+j\frac{2\omega L}{Z_0} \]
両辺の実部と虚部がそれぞれ等しくなるので2つの未知数$C,L$に対して2本の方程式が立ちます。 実部 \[ 1-2\omega^2LC =\frac{Z}{Z_0} \] 虚部 \[ \omega CZ=\frac{2\omega L}{Z_0} \]
得られた方程式を$C,L$について解くと \[ L=\frac{1}{2\omega}\sqrt{Z(Z_0-Z)} \] \[ C=\frac{1}{\omega Z_0}\sqrt{\frac{Z_0-Z}{Z}} \] となります。
$L$の計算結果に与えられたパラメータを代入すると$L=1.36[\mu H]$となり、答えは5です。
暗記しておけば即答できる類の問題ですが、計算を理解しておくことで最後の検算などに使えます。
計算のプロセスだけでも追えるようにしておきましょう。
R.3.7 無線工学B(1回目) A-9

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B A-9
マジックTと呼ばれる構造の導波管の問題です。 消去法で解くのが良いでしょう。
マジックTは構造的にはE面T分岐の導波管とH面T分岐の導波管なのでこれらの性質を抑えておけば解くことができます。
1
上述の通りの記述なので正しい
2
開口1はH面T分岐の導波管、開口2はE面T分岐の開口となっていてそれぞれ遮断されるので正しい。
3
開口1からの入力はH面T分岐の入力となるので、分岐した2つの出力は同相になります。(誤り)
4
2と同様で正しい。
5
開口2からの入力はE面T分岐の入力となるので、分岐した2つの出力は逆相になります。(正しい)
以上から答えは3です。
R.3.7 無線工学B(1回目) A-10
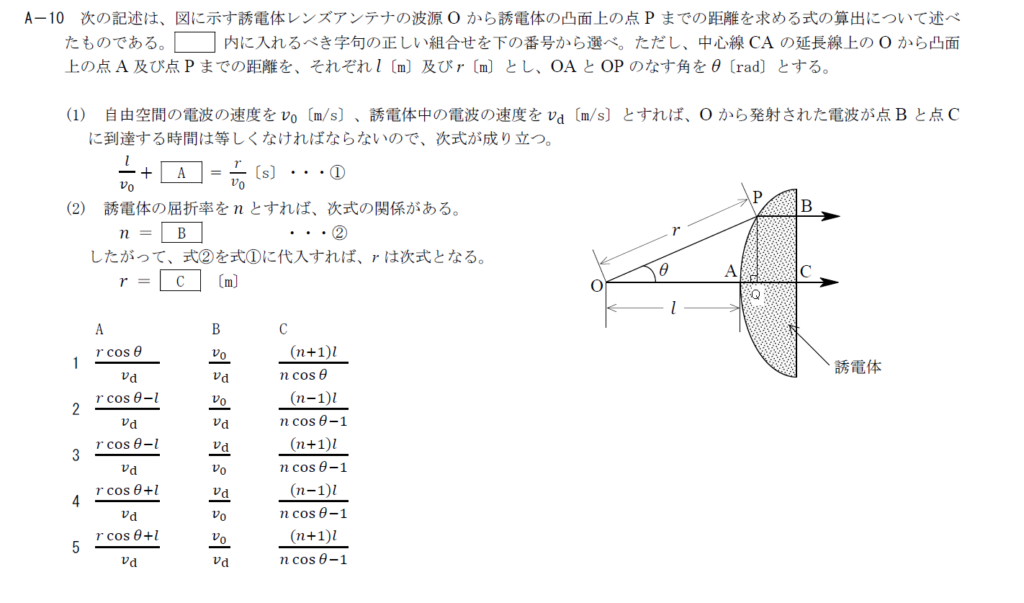
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年7月1回目 無線工学B A-10
誘電体レンズアンテナですが、ほとんど幾何学的な考えで解けます・
A
点Pから点Bへの経路と点Pから直線OCにおろした垂線と直線OCの交点Qから点Cへの経路は同じなので点Oから点Pへの到達時間と点Oから点Qへの到達時間が等しければいいはずです。
①の右辺は点Oから点Pへの到達時間となっており、$l/v_0$は点Oから点Aへの到達時間なので、空欄Aには点Aから点Qへの到達時間が入ります。 電波は速度$v_d$でAQ間を伝搬します。 OQ間の長さは$r\cos\theta$なので、到達時間は$\frac{r\cos \theta -l}{v_d}$です。
B
屈折率の定義は$n=\frac{v_0}{v_d}$なのでこの値がBに入ります。
C
①の式の両辺に$v_0$をかければ②の式が代入できるので、rについて解けば \[ r=\frac{(n-1)l}{n\cos\theta-1} \] となります。
以上から答えは2です。
まとめ
今回は先日行われた令和3年7月1回目の1陸技の無線工学BのA-6~10を解いてみました。 過去問が多く出題される1陸技の試験ですが、ここ最近は1回の試験で2回分の過去問が出るので過去問もはかどりますね。 試験が終わった直後ですが、次の試験を目指すならこの時期からであれば次の試験まで十分に時間が取れます。 1陸技を目指す方は頑張っていきましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人


コメント