1月の1陸技の試験無線工学BのA-11~15の問題について解説します。
R.3.1 無線工学B(1回目) A-11

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年1月1回目 無線工学B A-11
250[MHz]の電波の波長は1.2[m]です。
波長\(\lambda\)の半波長アンテナの実効長は\(\lambda/\pi\)となり、3線式折返し半波長ダイポールアンテナは半波長の素子が3本あるので、実効長はその3倍になります。
そのため\(l_e=3\frac{\lambda}{\pi}=1.15\)[m]です。
答えは3となります。
R.3.1 無線工学B(1回目) A-12

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年1月1回目 無線工学B A-12
ASR(空港監視レーダー)やARSR(航空路監視レーダ)などのアンテナはコセカント2乗特性のアンテナが使用されます。(A)
コセカント2乗特性の特徴として飛行機からの反射波の強度は等高度では距離によらず一定になります。(B)
ビーム幅は鋭くなります。(C)
以上から答えは4です。
R.3.1 無線工学B(1回目) A-13
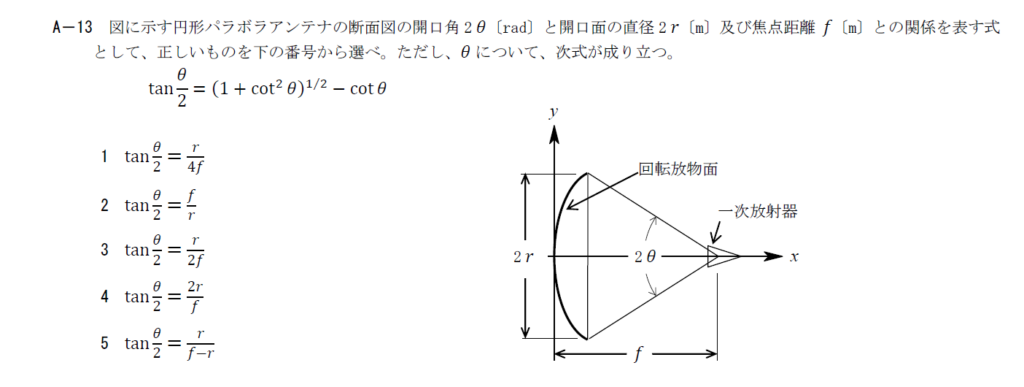
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年1月1回目 無線工学B A-13
パラボラアンテナの放物線上の任意の点を\((x_1,y_1)\)として、焦点からこの点に伸ばした直線とx軸のなす角を\(\theta_1\)とします。 すると\(\tan \theta_1=\frac{y_1}{f-x_1}\)となります。
パラボラアンテナの端点を\((x_0,r)\)とすると、三平方の定理から\(x_0=f-\sqrt{(f+x_0)^2-r^2}\)です。 \(x_0\)について解くと\(x_0=\frac{r^2}{4f}\)となります。
端点では\(x_1=\frac{r^2}{4f}, y_1=r, \theta_1=\theta\)なので \[ \tan \theta=\frac{4fr}{4f^2-r^2} \] です。 与えられた半角の公式に代入すると \[ \tan \frac{\theta}{2}=\frac{r}{2f} \] となります。
以上から答えは3となります。
R.3.1 無線工学B(1回目) A-14

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年1月1回目 無線工学B A-14
三角関数の定義から\(kR=(kR+h)\cos\theta\)です。(A)
弧度法では角度\(\theta\)は円周と円弧の長さの比に\(2\pi\)をかけた値となるので\(\theta=\frac{d}{kR}\)です。(B)
②の式に③の式を代入して、\(\theta\)についての関係式を作ります。 \(\theta\)はBで計算できているので、代入して計算すると\(d=\sqrt{2kRh}\)となります。
したがって、答えは5です。
R.3.1 無線工学B(1回目) A-15

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年1月1回目 無線工学B A-15
まず、伝搬のみについて考えていきます。 800[km]離れた地点に300[km]のF層で反射した電波が届くので電離層に到達前後で同じ直角三角形を考えることができます。 すなわち、直角を成す辺が400[km]と300[km]の直角三角形を考えれば良いので電波が通る距離は1000[km]となります。
1000[km]離れた地点の電界強度は\(E=120\pi\frac{GP}{4\pi d^2}\)から計算できます。 この式に与えられたパラメータを代入すると\(E=7\times10^{-5}[\rm{V/m}]=37[\rm{dB\mu V}]\)となります。
第二種減衰は7dBと与えられているので7dB引くと30[dB\(\mu\)V]となります。
以上から答えは5です。
まとめ
今回は令和3年1月1回目の1陸技の無線工学BのA-11~15を解いてみました。 受かった人も来年頑張る人も気になっている問題もあったのではないでしょうか。 飽きるまで解いて記事にしていきたいと思います。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人


コメント