1月の1陸技の試験無線工学BのA-16~20の問題について解説します。
R.3.1 無線工学B(1回目) A-16

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年1月1回目 無線工学B A-16
誤ったものを選ぶタイプの問題です。
この問題については明らかにおかしい選択肢があるので即答しちゃっても良さそうです。 答えは3です。
この問題は最悪他の選択肢の内容について覚えてなくても答えを出せます。 3の選択肢では2つの矛盾があります。
まず、船舶用の衛星通信では船舶に対して衛星がどこにあるか分からないのでビーム幅が狭いと衛星通信が難しくなります。
また、文中にも矛盾があるためこれで答えられると思います。 もしビーム幅が狭いアンテナを使っている場合、海面反射波を拾いにくくなるはずなので選択肢の主張が矛盾しています。
R.3.1 無線工学B(1回目) A-17
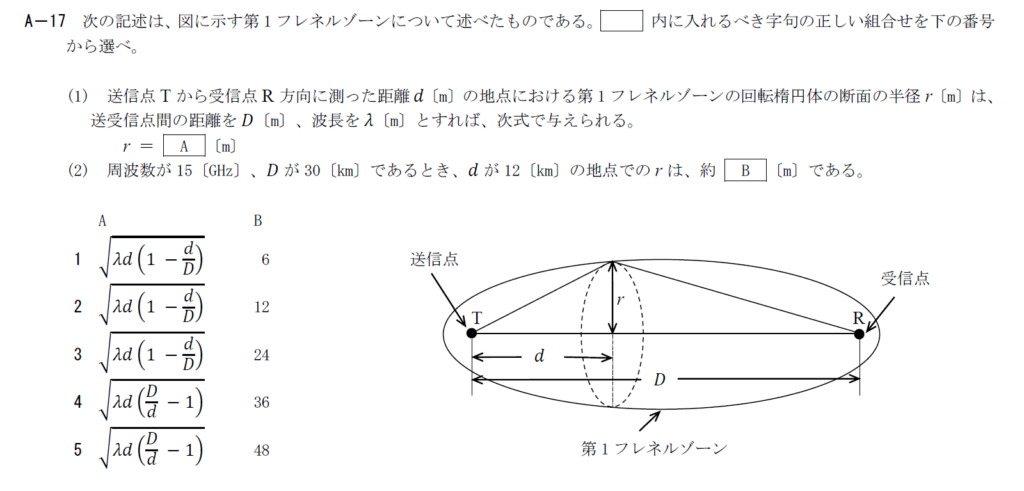
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年1月1回目 無線工学B A-17
第1フレネルゾーンでは直接波と回折波の経路差が1/2波長になります。
まず、経路差\(\delta l\)を求めましょう。
\[ \delta l =\sqrt{d^2+r^2}+\sqrt{(D-d)^2+r^2}-D \]
d>>r, D>>rとすると
\[ \delta l =d(1+\frac{1}{2}\frac{r^2}{d^2})+(D-d)(1+\frac{1}{2}\frac{r^2}{(D-d)^2})-D \\ =\frac{r^2}{2}(\frac{1}{d}+\frac{1}{D-d}) \]
以上から\(r=\sqrt{\lambda d (1-d/D)}\)となります。(A)
Aの式に与えられた値を代入すると12[m]となります。(B)
以上から答えは2です。
R.3.1 無線工学B(1回目) A-18

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年1月1回目 無線工学B A-18
利得\(G_1\)のアンテナは等方向性アンテナに対して、最大放射方向の電力が\(G_1\)倍の放射になります。
\(P_t\)[W]の電力の電波を利得\(G_1\)のアンテナで放射した時距離dの点での電力密度は次のように表せます。
\[ \frac{G_1P_t}{4\pi d^2}[\rm{W/m^2}] \]
これを実効面積\(\frac{\lambda^2}{4\pi}G_2\)のアンテナで受信するので、 \[\frac{P_r}{P_t}=\left(\frac{\lambda}{4\pi d}\right)^2G_1G_2\] となります。(A)
\(G_1=G_2=G\)を代入してGについて解くと\(G=\frac{4\pi d}{\lambda}\sqrt{P_r/P_t}\)となります。(B)
反射させて送受信を同じアンテナを使うので反射鏡です。(C)
以上から答えは4となります。
R.3.1 無線工学B(1回目) A-19

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年1月1回目 無線工学B A-19
ハイトパターンの測定に関する問題です。
まず、直接波と反射波の経路長を求めましょう。 A-17と同様に\(d>>h_1,h_2\)と考えます。
直接波 \[ \sqrt{d^2+(h_1-h_2)^2}\simeq d\left(1+\frac{(h_1-h_2)^2}{2d^2}\right) \]
反射波 受信側のアンテナが地面を境界に鏡で映した位置にあると考えると最短距離になります。 \[ \sqrt{d^2+(h_1+h_2)^2}\simeq d\left(1+\frac{(h_1+h_2)^2}{2d^2}\right) \]
上記から \[\delta l=\frac{(h_1+h_2)^2-(h_1-h_2)^2}{2d}=\frac{2h_1h_2}{d}\] となります。(A)
受信電界強度は\(E\propto \sin(\frac{2\pi}{\lambda}\delta l)\)となるので\(\sin(\frac{2\pi h_1h_2}{\lambda d})\)です。(B)
サインが最大になるのは\(\frac{2\pi h_1h_2}{\lambda d}=\pi(1/2+n)\)の時です。
\(h_{m1}とh_{m2}\)の時の条件を当てはめると\(\delta h=\frac{\lambda d}{2h_1}\)となります。(C)
したがって、答えは1です。
R.3.1 無線工学B(1回目) A-20
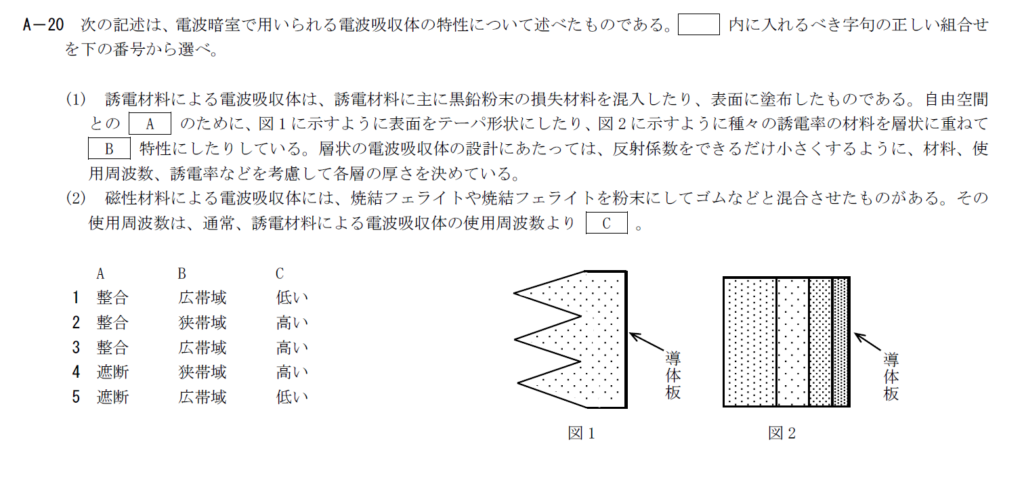
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年1月1回目 無線工学B A-20
電波暗室に使用する誘電体は自由空間と整合を取る形状とします。(A)
種々の材料を層状に重ねることで広帯域特性になります。(B)
磁性材料は誘電材料と比較すると使用周波数が低く帯域が狭くなります。(C)
以上から答えは1です。
まとめ
今回は令和3年1月1回目の1陸技の無線工学BのA-16~20を解いてみました。 受かった人も来年頑張る人も気になっている問題もあったのではないでしょうか。 飽きるまで解いて記事にしていきたいと思います。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人


コメント