R.3.12 無線工学 A-1
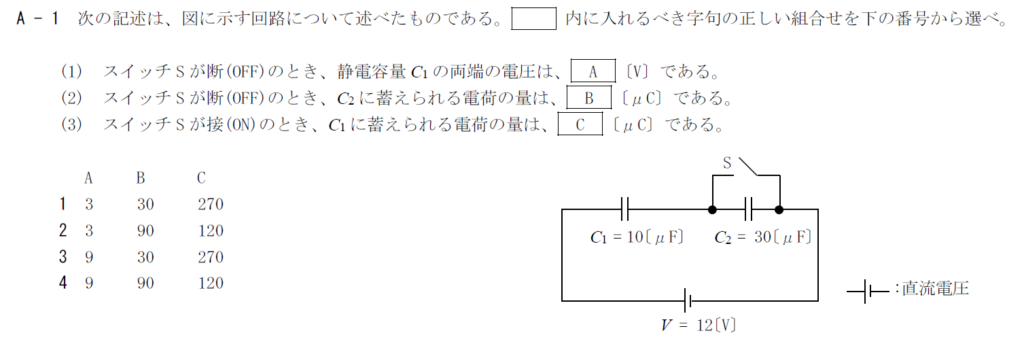
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年12月 無線工学A-1
A
図の回路では$C_1$と$C_2$には同じ電荷が蓄えられます。 $C_1V_1=C_1V_2$なので$\frac{C_1}{C_2}=\frac{V_2}{V_1}$となるので、$C_1$の両端の電圧は全体の$\frac{30}{10+30}=\frac{3}{4}$倍の9Vです。 そのため、Aには9が入ります。B
$C_2$には3Vの電圧がかかるので、$30 \times 3=90[\rm{\mu C}]$となります。 そのため、Bには90が入ります。C
SがOFFとなると$C_2$が短絡され、$C_1$にだけ12Vがかかることになります。 $C_1$に蓄えられる電荷は$120[\rm{\mu C}]$です。 そのため、Cには120が入ります。 以上から答えは4です。R.3.12 無線工学 A-2
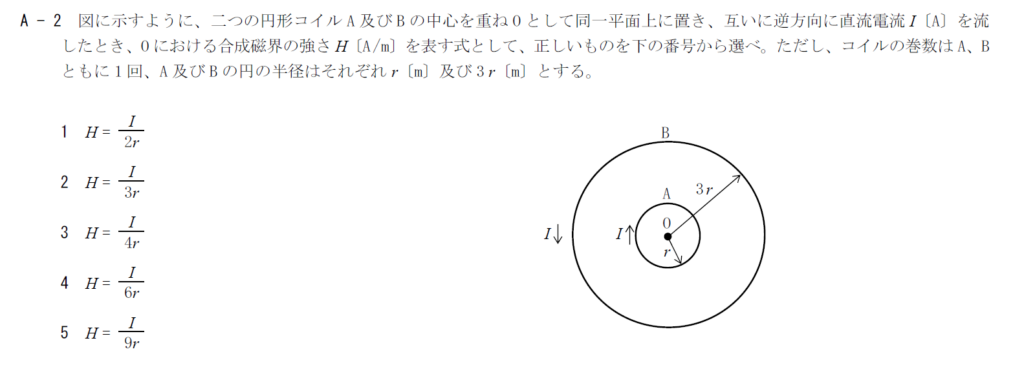
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年12月 無線工学A-2
R.3.12 無線工学 A-3
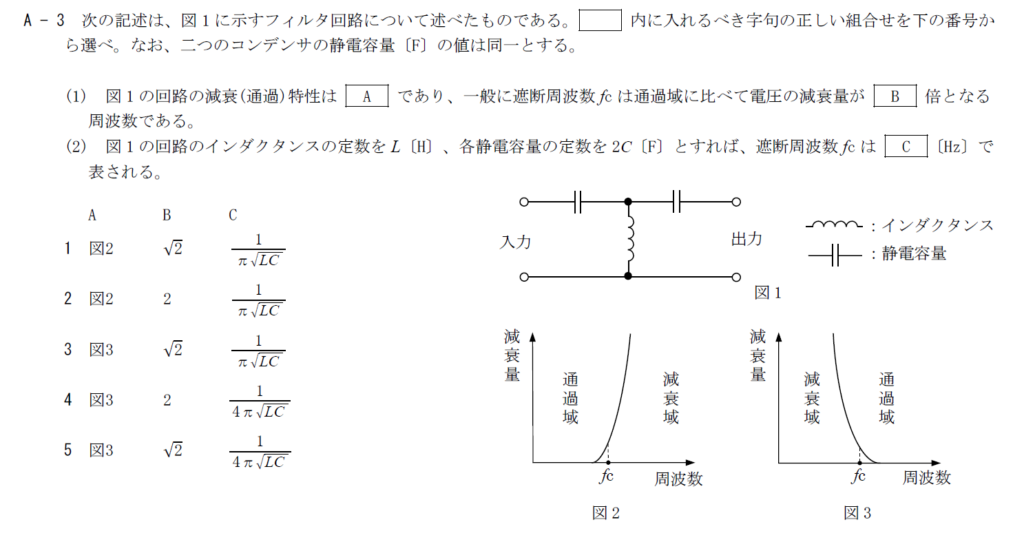
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年12月 無線工学A-3
A
図1ではコイルがグランド側につながる様になっています。 低い周波数ほどコイルを流れやすく、出力に現れないのでこの回路はハイパスフィルタと考えることができます。 ハイパスフィルタは文字通り高い周波数が通過するので図3が通過特性です。 そのため、Aには図3が入ります。B
遮断周波数は通過域に比べて電力の減衰量が2倍になる周波数です。 電圧にすると$\sqrt{2}$倍です。 そのため、Bには$\sqrt{2}$が入ります。C
通過特性が$1/\sqrt{2}$になるように周波数を計算すると$\frac{1}{4\pi \sqrt{LC}}$となります。 そのため、Cには$\frac{1}{4\pi \sqrt{LC}}$が入ります。 以上から答えは5です。R.3.12 無線工学 A-4
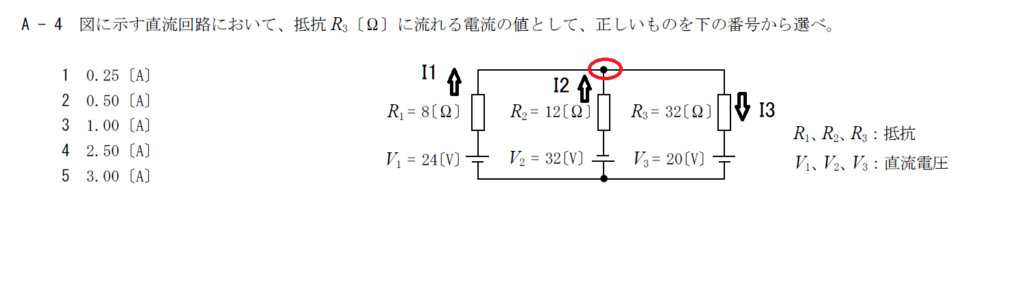
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年12月 無線工学A-4
R.3.12 無線工学 A-5
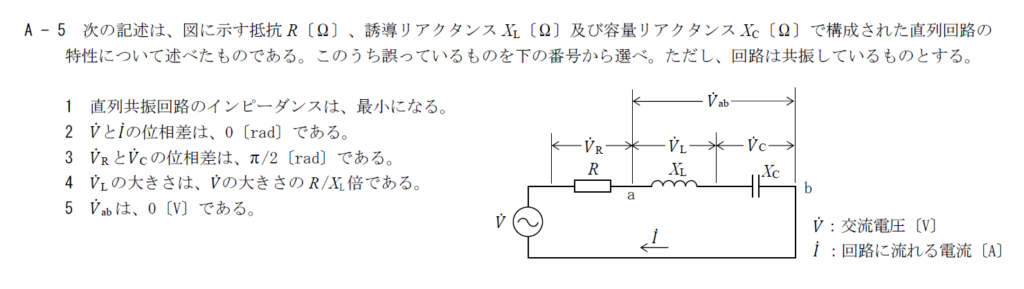
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R3年12月 無線工学A-5
1
直列共振回路のインピーダンスは$Z=R+j(X_L+X_C)$です。 直列共振回路が共振するとインピーダンスの虚部がゼロになるのでインピーダンスは最小になり、この選択肢は正しいです。2
電圧の位相がコイルで90°遅れて、コンデンサで90°進むので電圧と電流の位相差はゼロとなり、この選択肢は正しいです。3
コンデンサにかかる電圧と抵抗にかかる電圧の位相差は$\pi/2$となり、この選択肢は正しいです。4
$V_L$は$V_L=\frac{X_L}{R^2+(X_L+X_C)^2}V$となります。 そのため、この選択肢が誤りです。5
問題文からこの回路は共振しているのでab間のインピーダンスが0となります。 そのため、$V_{ab}=0$で、この選択肢は正しいです。 以上から答えは4です。まとめ
1陸技の7月の無線工学AとBを解き終わったので、最近難化傾向と言われる1アマの問題を解いてみました。 1陸技と比べると基本的な問題が出ますが、たしかに私が受けた10年前より難しくなっている気もします。 そろそろアマチュア無線家としても復活していきたいところです。 勉強法 第一級陸上無線技術士の勉強法とおすすめ参考書参考文献
リンク
電磁気学をちゃんと学びたい人向け
リンク
上の難易度が高い人
リンク
リンク


コメント
R.3.12 無線工学 A-1のB及びCの回答の単位は、µCではないでしょうか
ご指摘ありがとうございます。
μCで正しいです。修正しました。