令和4年1月の1陸技2回目の試験、無線工学AのA-11～15の問題について解説します。
R.4.1 無線工学A（2回目） A-11
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-11
レーダーのパルス圧縮技術の原理に関する問題です。
この問題では線形周波数変調（チャープ）方式について主に記述されています。
パルス幅を広くすると尖頭電力はは小さくても平均電力が大きくなるので、最大探知距離を大きくできます。
その一方で、パルス間隔が広くなるので分解能が悪くなってしまいます。
このように一般には距離分解能と最大短距離はトレードオフの関係にあり、これを解消しようとする技術がパルス圧縮技術です。
A
遅延時間の周波数特性が送信時と逆のフィルタを用いることでパルス幅を狭くする事ができます。
送信時と逆の周波数特性にすることによって、パルス内のある1点でのみ強い信号が取り出せるのでこれによりパルスが圧縮されることになります。
そのため、Aには「逆」が入ります。
B
電力が$T\Delta f$倍となるので、振幅は$\sqrt{T\Delta f}$倍となります。
そのため、Bには「$\sqrt{T\Delta f}$」が入ります。
この空欄は無次元量が入らないといけないので選択肢から無次元のものを選んで$\sqrt{T\Delta f}$と決めることもできます。
C,D
(3)はこの問題の冒頭で説明したような距離分解能と最大探知距離の関係について言及した文章です。
上述の通り、パルス圧縮技術は低い送信電力で広いパルス幅の信号を用いて、本来望まれる大電力で狭いパルスを送信するのと同じ効果を得ようという技術です
そのため、Cには「広」、Dには「狭」が入ります。
以上から答えは2です。
R.4.1 無線工学A（2回目） A-12
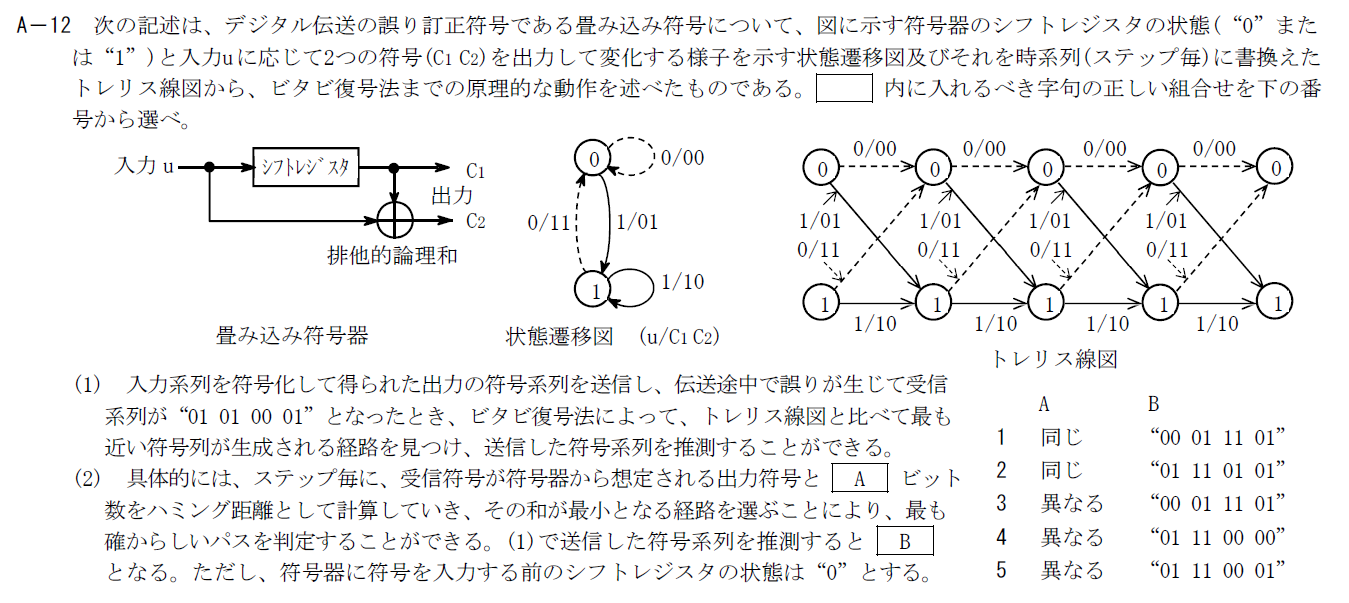
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-12
畳み込み符号とビタビ復号によるその復号に関する問題です。
A
ビタビ復号は簡単に言うと、発生しうる符号をトレリス線図で作って、その符号のうち受信した符号に最も近いものを正しい符号とするというアルゴリズムです。
ビタビ復号では符号同士の「近さ」の指標としてハミング距離を計算します。
ハミング距離は符号同士で異なるビットの数と定義できます。
そのためAは「異なる」が入ります。
B
Aが「異なる」となっている3~5だけ見てもいいですが、一応全部見ておきましょう。
| 番号 | 符号 | 距離 |
|---|---|---|
| 1 | “00 01 11 01” | 3 |
| 2 | “01 11 01 01” | 2 |
| 3 | “00 11 01 01” | 3 |
| 4 | “01 11 00 00” | 2 |
| 5 | “01 11 00 01” | 1 |
一番ハミング距離が小さいのは5の”01 11 00 01″です
以上から答えは5です。
R.4.1 無線工学A（2回目） A-13
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-13
デジタル信号のアイパターンについて正しいものを選ぶ問題です。
1陸技では誤ったものを選ぶ問題が多いですが、今回は正しいものを選ぶ問題なので気をつけましょう。
ここではそれぞれの選択肢を見ていくことにします。
1
アイパターンの横軸は時間なので、アイパターンの横の開き具合は時間による変動に対する余裕を示します。
1の時間による変動に対する余裕とは「識別タイミングの劣化に対しての余裕」と考えることができるので、この選択肢は正しいです。
2
アイパターンはすべてのパルス波形の重ね合わせです。
各ビットを識別しているわけはないので誤り訂正の符号化率を知ることはできません。
そのため、この選択肢は誤りです。
3
図では識別時刻に4値がきれいに分かれているので符号間干渉により識別できない状態ではありません。
そのため、この選択肢は誤りです。
4
識別時刻で4値に分かれているので2値ではなく、4値のアイパターンです。
そのため、この選択肢は誤りです。
5
時間の長さ$t$の間には2シンボル時間となっています。
そのため、この選択肢は誤りです。
以上から答えは1です。
R.4.1 無線工学A（2回目） A-14
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-14
ASRやARSRに関する問題です。
A
ASRやARSRはSSRと組み合わせて使用することで3次元的に航空機の位置を把握できます。
そのため、Aには「SSR(航空用二次監視レーダー)」が入ります。
B
MTIでは航空機で反射された電波の位相がドプラ効果で変化することを利用しています。
トムソン効果は1つの金属上で温度差があるところに電流を流した時に熱の発生や吸収が起きる現象です。
この問題の文脈にはそぐわない語句です。
そのため、Bには「ドプラ効果」が入ります。
C
反射パルスのタイミングを調整したものと次の周期の信号との差をとることで移動目標以外の効果を消すことができます。
そのため、Cには「差」が入ります。
以上から答えは2です。
R.4.1 無線工学A（2回目） A-15
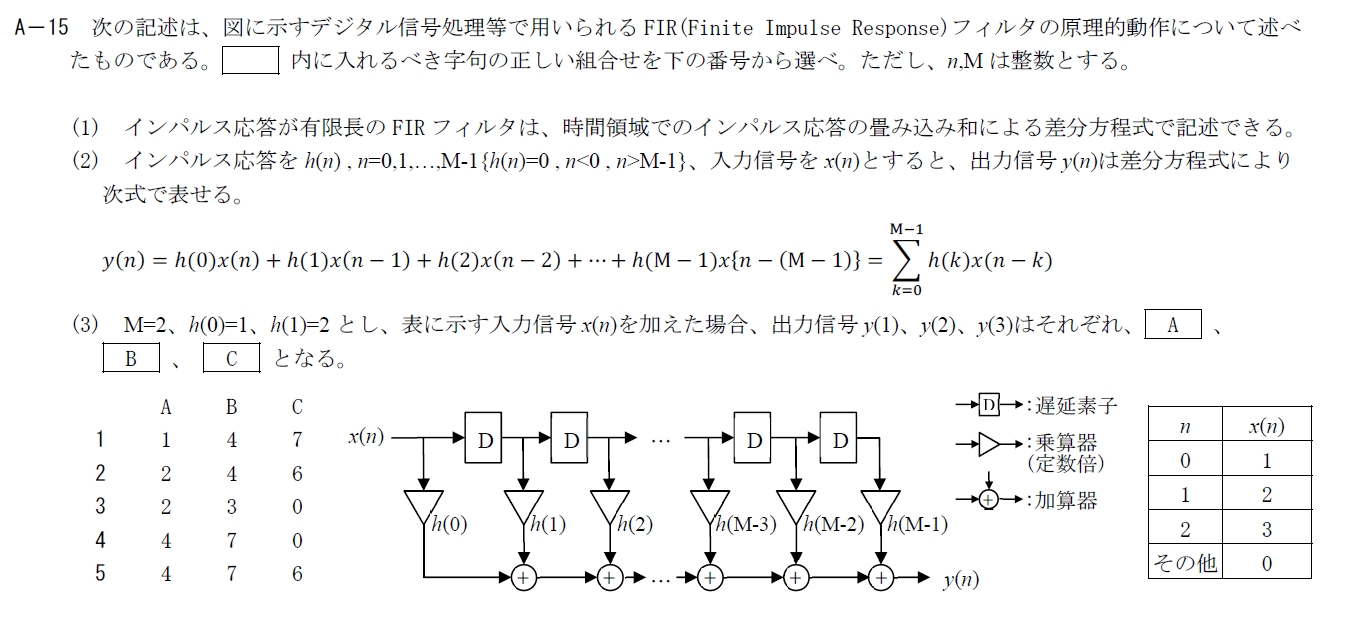
出典：公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-15
FIRの原理的動作に関する計算問題です。
(3)で与えられた条件を(2)の式に代入することで計算することができます。
(2)で
\[
y(n)=\sum^{M-1}_{k=0}h(k)x(n-k)
\]
と与えられているので
\[
y(1)=h(0)x(1)+h(1)x(0)=4 \\
y(2)=h(0)x(2)+h(1)x(1)=7 \\
y(3)=h(0)x(3)+h(1)x(2)=6
\]
となります。
この結果から答えは5です。
まとめ
今回は令和4年1月2回目の1陸技の無線工学AのA-11~15を解いてみました。
無線工学Aでは問題に沿った計算を行う問題も多く出題されます。
この類の問題は誘導に沿って計算すればいいので難しそうに見えて意外と簡単なことも多いです。
申込期間も終わり、そろそろ試験勉強も本格的になってきた頃でしょう。
本サイトも活用して合格を勝ち取ってください。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人
コメント