R.4.1 無線工学A(2回目) A-16

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-16
A
入力信号の周波数が標本化周波数$f_S$の1/2である$f_O$を超えると折り返し雑音が発生します。 そのため、Aには「折り返し雑音」が入ります。B
折り返し雑音は$f_O$を中心に周波数が低い側に折り返された形となって現れます。 そのため、Bには「低い」が入ります。C
アパーチャ効果は標本化パルスが有限の幅を持つパルスであるときに発生する現象です。 理想的なインパルスで標本化したときは、その周波数特性は周波数によらず1となりますが、有限の幅を持つパルスで標本化を行うと周波数特性がsinc関数になり、周波数が高いほど周波数特性が悪くなります。 そのため、Cには「高域の周波数成分」が入ります。 一応計算を載せておきます。 理想的なインパルスのインパルス応答$f(t)$は$f(t)=\delta (t)$です。 これをフーリエ変換すると \[ F(\omega)=\int^{+\infty}_{-\infty}\delta (t)e^{-j\omega t}dt \\ =1 \] となります。 一方、有限の幅$T$を持つパルスの場合、インパルス応答は \[ f(t)=\left\{ \begin{array}{} 1/T & (-T/2\leq t \leq +T/2) \\ 0 & \rm{other} \end{array} \right. \] です。 同様にフーリエ変換すると \[ F(\omega)=\int^{+\infty}_{-\infty}f(t)e^{-j\omega t}dt \\ \int^{+T/2}_{-T/2}\frac{1}{T}e^{-j\omega t}dt \\ =-\frac{1}{j\omega T}(e^{-j\omega T/2}-e^{j\omega T/2}) \\ =\frac{2}{\omega T}\sin \left( \frac{\omega T}{2}\right) \\ =\frac{\sin \left( \frac{\omega T}{2}\right)}{\frac{\omega T}{2}} \] となり、周波数が高いほど周波数特性が劣化していることがわかります。 以上から答えは2です。R.4.1 無線工学A(2回目) A-17
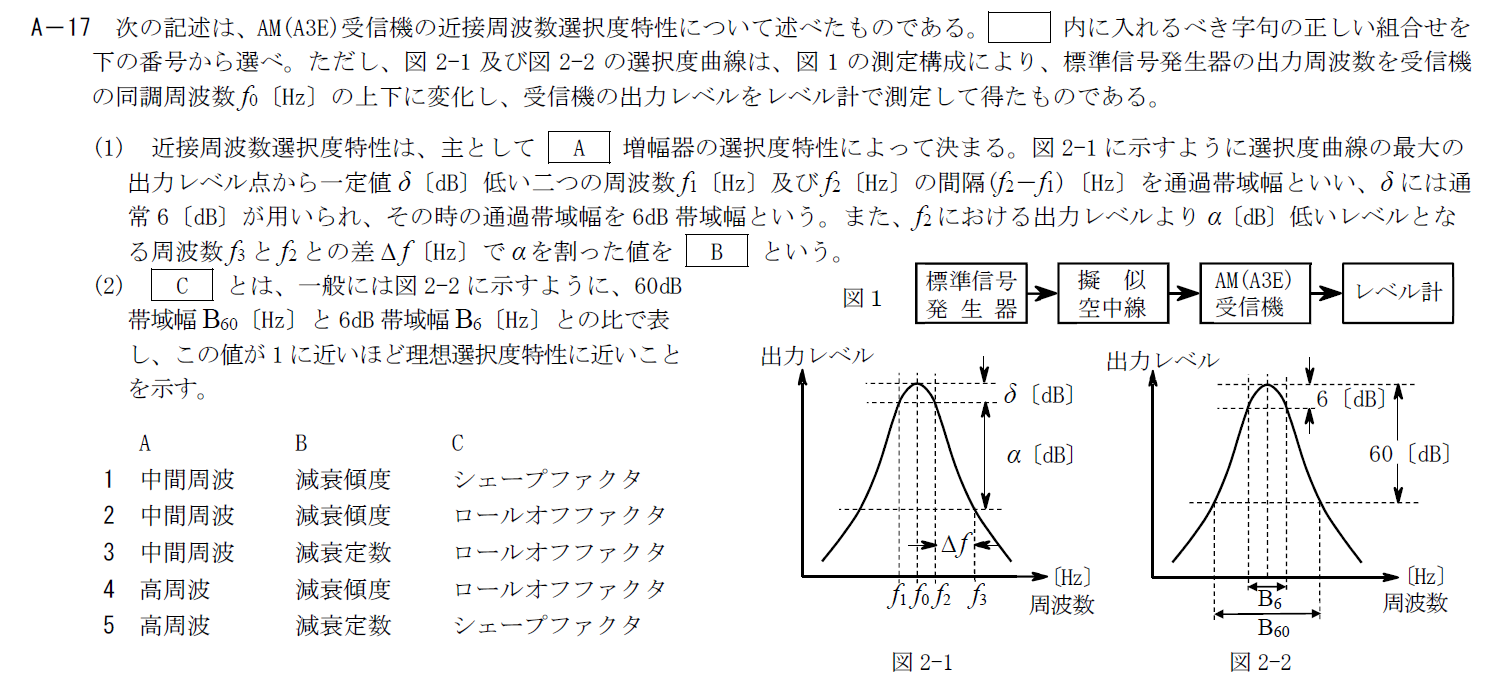
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-17
A
近接周波数選択度特性は中間周波増幅器のやBPFの選択度特性によって決まります。 アンテナから入力される高周波信号より低い中間周波数のほうが周波数選択度特性を良くしやすいので、初段の高周波増幅器では希望の周波数帯以外をざっくり落として、 中間周波数で近接の不要な信号を除去するのが一般的です。 そのためAは「中間周波」が入ります。B
$\Delta f$で$\alpha$を割ると周波数特性の傾きを表すことに成るので、Bには「減衰傾度」が入ります。C
(2)の説明はシェープファクタに関する説明となっています。 $B_6$と$B_{60}$の比は周波数特性の形がどれくらい理想に近いかを表すので、シェープファクタと考えるのが適当です。 そのため、Cには「シェープファクタ」が入ります。 以上から答えは1です。R.4.1 無線工学A(2回目) A-18
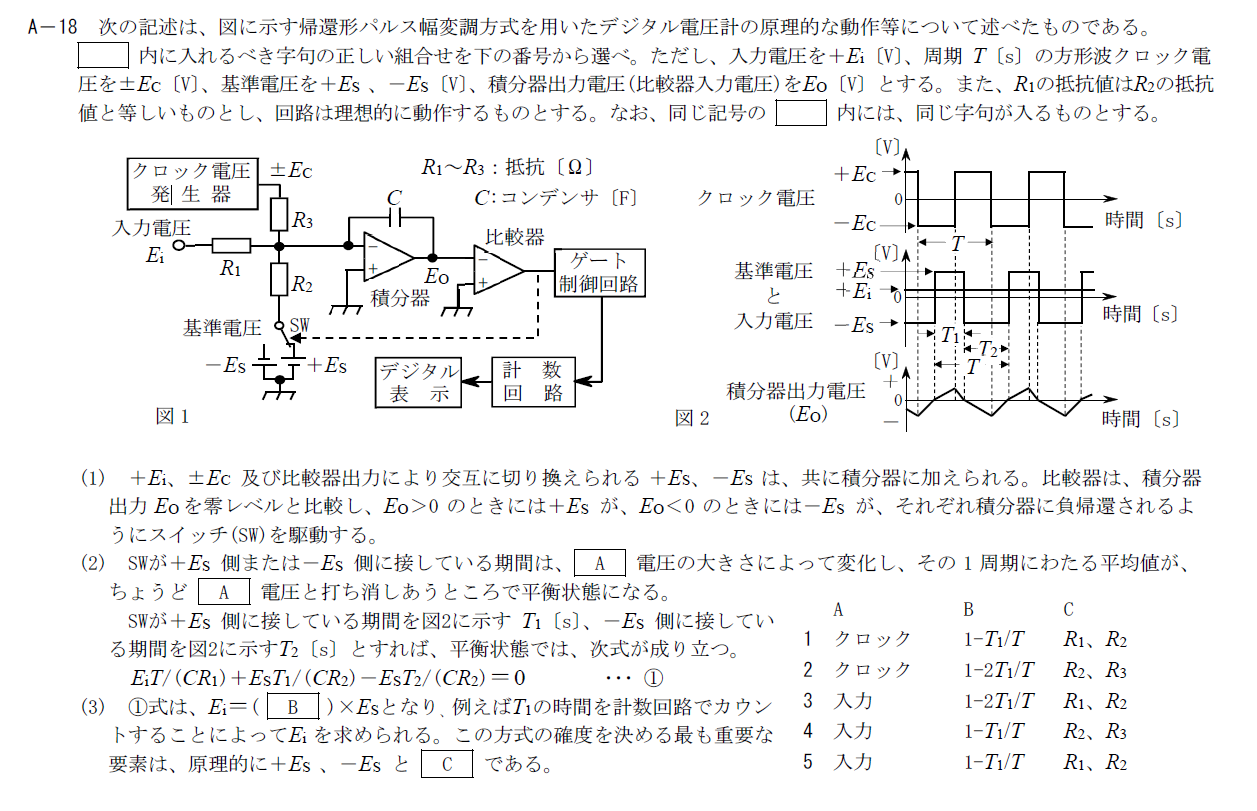
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-18
A
(2)の説明は主語がないので少しわかりにくいかもしれません。 (1)の文脈から$E_O$の変化について説明していると考えるのが妥当でしょう。 クロック電圧はデューティ比50%なので、積分器を通すと出力はゼロになります。 そのため、SWが基準電圧に接している期間は$E_O$によって変化します。 以上のことからAには「入力」が入ります。B
①の式を$E_i$について解くと \[ E_i=\frac{R_1}{R_2}\frac{T_2-T_1}{T}E_S \] となります。 問題文から$R_1=R_2$、$T_2=T-T_1$なので、 \[ E_i=\left( 1-\frac{2T_1}{T}E_S\right) \] となります。 そのため、Bには「$1-2T_1/T$」が入ります。C
Bでの$E_i$の計算結果からも分かるように、$E_i$の計算に寄与しているのは$R_1$と$R_2$です。 そのため、Cには「$R_1$、$R_2$」が入ります。 以上から答えは3です。R.4.1 無線工学A(2回目) A-19

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-19
R.4.1 無線工学A(2回目) A-20
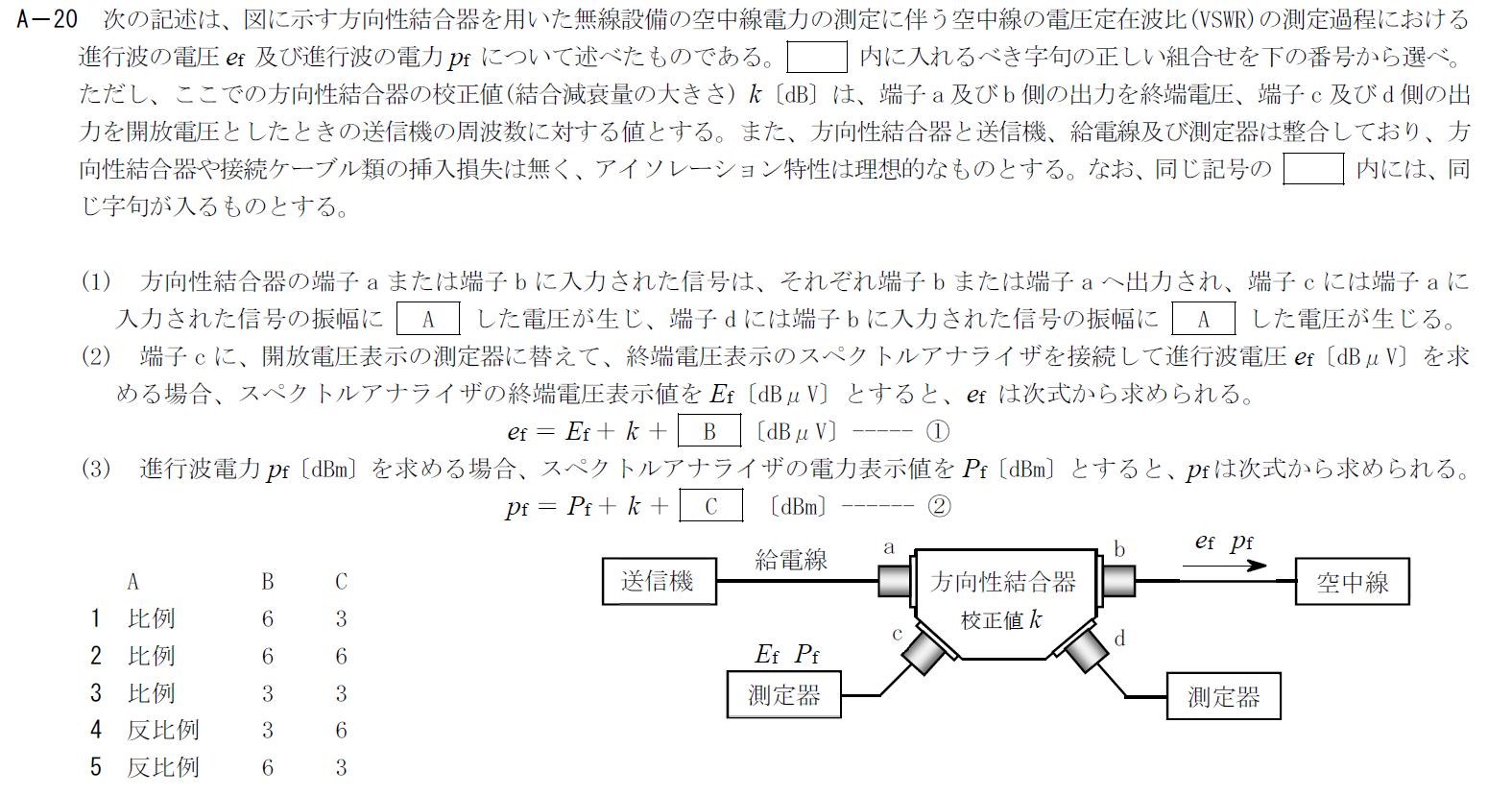
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年1月2回目 無線工学A A-20
A
図中の端子cには端子aに入力された信号の振幅に比例した電圧が生じます。 端子bと端子dに関しても同様です。 そのため、Aには「比例」が入ります。B
端子cは終端されているのでそこで測定される電圧は1/2倍となり、6[dB]下がります。 $E_f=e_f-k-6[\rm{dB\mu V}]$なので、 \[ e_f=E_f+k+6[dB\mu V] \] となります。 そのため、Bには「6」が入ります。C
まず、$p_f$の真数での表記を考えます。 \[ p_f(\rm{真数})=\frac{e_f^2}{Z_0} \] ここで、$Z_0$は給電線等の特性インピーダンスです。 単位をdBmに直すと次のようになります。 \[ p_f=10\log \frac{e_f^2}{Z_0} \\ =e_f -10\log Z_0 \\ =E_f+k+6-10\log Z_0 \\ =(E_f -10\log Z_0)+k+6 \\ =P_f+k+6 \] となるため、Cには「6」が入ります。 以上から答えは2です。まとめ
今回は令和4年1月2回目の1陸技の無線工学AのA-16~20を解いてみました。 無線工学Aでは、測定原理に関する問題も多く出題されます。 問題文をしっかり読めばその中に答えにつながるヒントが隠されていることも多いです。 見たことがない内容だと諦めずに解いてみましょう。 申込期間も終わり、そろそろ試験勉強も本格的になってきた頃でしょう。 本サイトも活用して合格を勝ち取ってください。 勉強法 第一級陸上無線技術士の勉強法とおすすめ参考書参考文献
リンク
電磁気学をちゃんと学びたい人向け
リンク
上の難易度が高い人
リンク
リンク



コメント