令和4年7月の1陸技の試験2回目の無線工学BのA-6~10の問題について解説します。
R.5.1 無線工学B(2回目) A-6
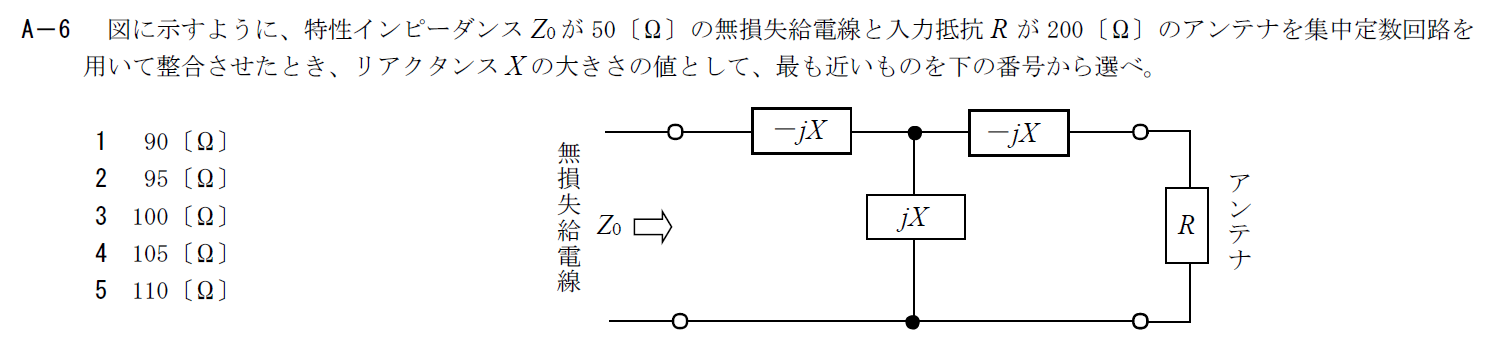
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学B A-6
T型整合回路に関する問題です。
給電線から見たインピーダンス$Z$を計算して、それが給電線の特性インピーダンス$Z_0$と等しくなるように$X$を決めます。
実際に$Z$を計算してみると \[ Z=-jZ+\frac{jX(R-jX)}{R}=\frac{X^2}{R} \] となります。
$Z=Z_0$なので \[ X=\sqrt{Z_0R} \] です。
$Z_0=50, R=200$を代入すると \[ X=100[\rm{\Omega}] \] となります。
以上から答えは3です。
R.5.1 無線工学B(2回目) A-7

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学B A-7
給電線の特性インピーダンスと電波の伝搬速度から単位長当りのインダクタンスを求める問題です。
単位長当りのインダクタンスを$L$、静電容量を$C$として問題文からこれらについての連立方程式を立てましょう。 \[ \sqrt{\frac{L}{C}}=Z_0 \\ \frac{1}{\sqrt{LC}}=0.7c \] ここで$c$は真空中での光速です。
$C$を消去して$L$について解くと \[ L=\frac{Z_0}{0.7c}=\frac{50}{2.1\times 10^8} \\ =23.4 \times 10^{-8}\rm{[H/m]}=0.24\rm{[\mu H/m]} \] となります。
以上から答えは4です。
ちなみに$C$は \[ C=\frac{L}{Z_0^2}=\frac{1}{Z_0\times 0.7c}=9.52 \times 10^{-11}\rm{[C/m]}=95.2\rm{[pC/m]} \] です。
R.5.1 無線工学B(2回目) A-8

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学B A-8
給電線の特性インピーダンス$Z_0$と負荷インピーダンス$Z_R$を接続したときの反射係数と電圧定在波比(VSWR)を計算する問題です。
値が違って同じ問題が令和3年7月1回目のA-7で出題されています。 こちらの記事もご参照ください。

反射係数$\Gamma_V$は次の通りです。 \[ \Gamma_V=\frac{Z_R-Z_0}{Z_R+Z_0}=\frac{25-j75-50}{25-j75+50}=-\frac{25(1+j3)}{75(1-j)}=\frac{1}{3}(1-j2) \]
電圧定在波比$S_V$は反射係数を使って \[ S_V=\frac{1+|\Gamma_V|}{1-|\Gamma_V|}=\frac{3+\sqrt{5}}{3-\sqrt{5}} \] となります。
以上から答えは3です。
R.5.1 無線工学B(2回目) A-9

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学B A-9
導体中への平面波が浸透するときの表皮厚さ(深さ)に関して誤った選択肢を選ぶ問題です。
同様の問題が令和3年7月2回目のA-9で出題されています。

また、同じ表皮厚さに関する問題で、穴埋め形式の問題が令和4年1月2回目のA-8で出題されています。 こちらの記事も参考にしてください。

誤った選択肢は4です。
減衰定数が小さいほど導体中を平面波が減衰しにくくなるので表皮は厚く(深く)なります。
以上から答えは4です。
R.5.1 無線工学B(2回目) A-10
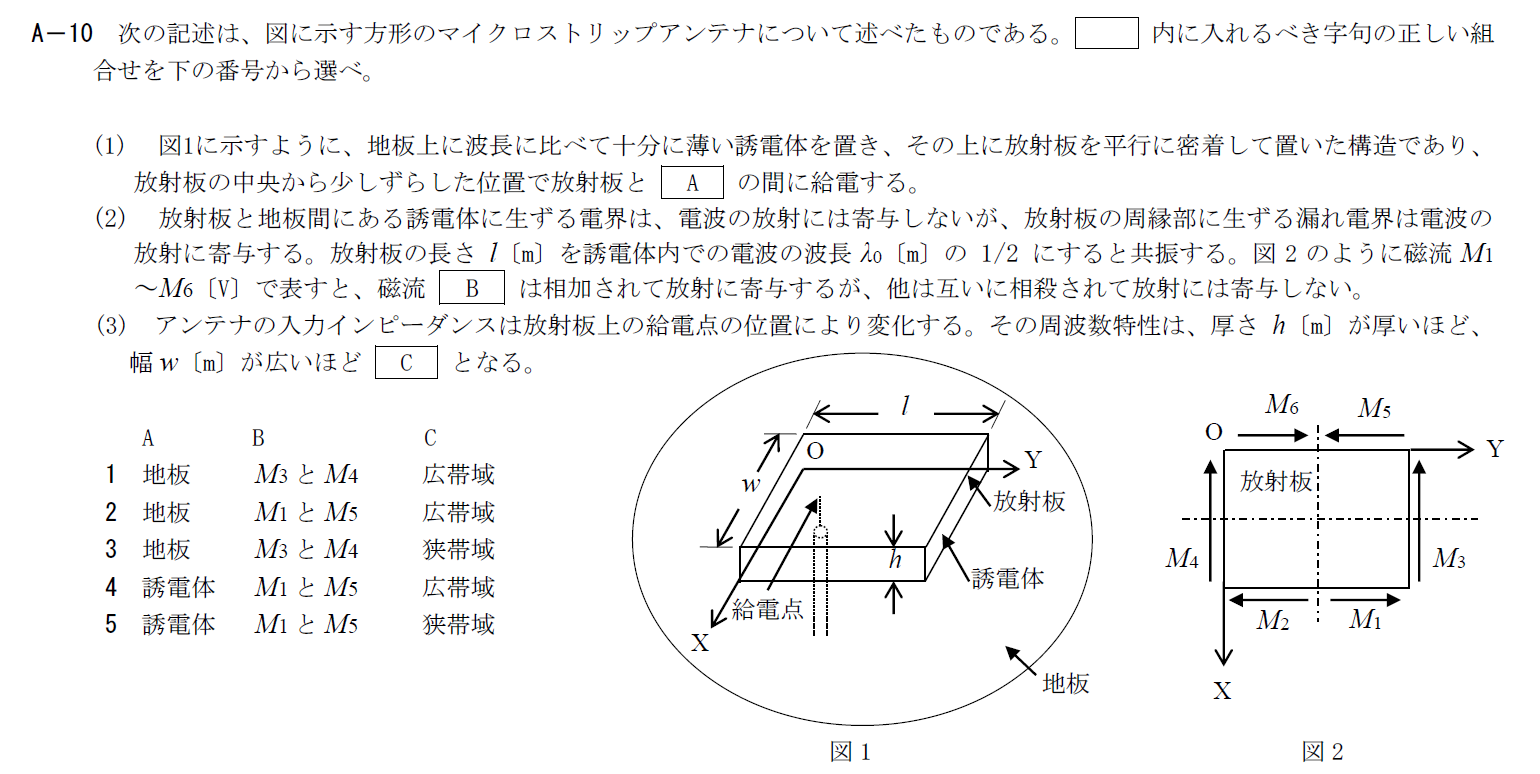
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学B A-10
マイクロストリップアンテナに関する問題です。
同様の問題が令和3年7月2回目のB-3と令和4年7月2回目のB-3で出題されています。 上記の問題はB問題なので空欄の数が多いのでこちらの解説も参考にしてください。


答えは
- A:地板
- B:$M_3$と$M_4$
- C:広帯域
で、1です。
まとめ
今回は令和5年1月の無線工学B(2回目)の試験A-6~A-10の問題について解説しました。 合成抵抗を求める必要がある問題や連立方程式を立てる必要がある問題など面倒な問題も多いです。 しっかり問題を読んで解いていきましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント