令和5年1月の1陸技の試験2回目の無線工学AのA-1~5の問題について解説します。
R.5.1 無線工学A(2回目) A-1

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-1
OFDMの基本原理に関する問題です。
A
$n$番目の搬送波は$e^{j2\pi nf_st}$なので、周波数は$nf_s$です。
そのため、$T$の期間に$n$周期分含まれるのでAには「$n$」が入ります。
B
$d_n$は複素データシンボルなので$d_n=A_ne^{\phi_n}$の形で表せます。 $\phi_n$が各搬送波成分の位相に相当するのでここの位相は異なる値になります。
そのため、Bには「異なる」が入ります。
C
マルチキャリアでは複数の搬送波がそれぞれ変調されるので、各搬送波に電力が分散されます。 ピークと平均の電力の差は小さくなるのでPAPRは高くなります。
上記のことからCには「高く」が入ります
以上から答えは1です。
R.5.1 無線工学A(2回目) A-2

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-2
$\alpha =0.5$のロールオフフィルタでは$fT=0.75$で伝達関数がゼロになります。 ここで$1/T$がシンボルレート、$f$は周波数です。
帯域幅はI信号またはQ信号のシンボルレートに依存します。いずれも同じシンボルレートなのでI信号だけ考えましょう。
I信号は1シンボル当たり2bitなのでビットレート$R$は周波数です。 \[ R=\frac{2}{T}=\frac{2f}{0.75}=24\rm{[Mbps]} \] となります。
ロールオフフィルタの特性については令和5年1月1回目B-5の内容が参考になります。 下記の記事も参考にしてください。

以上から答えは4です。
R.5.1 無線工学A(2回目) A-3
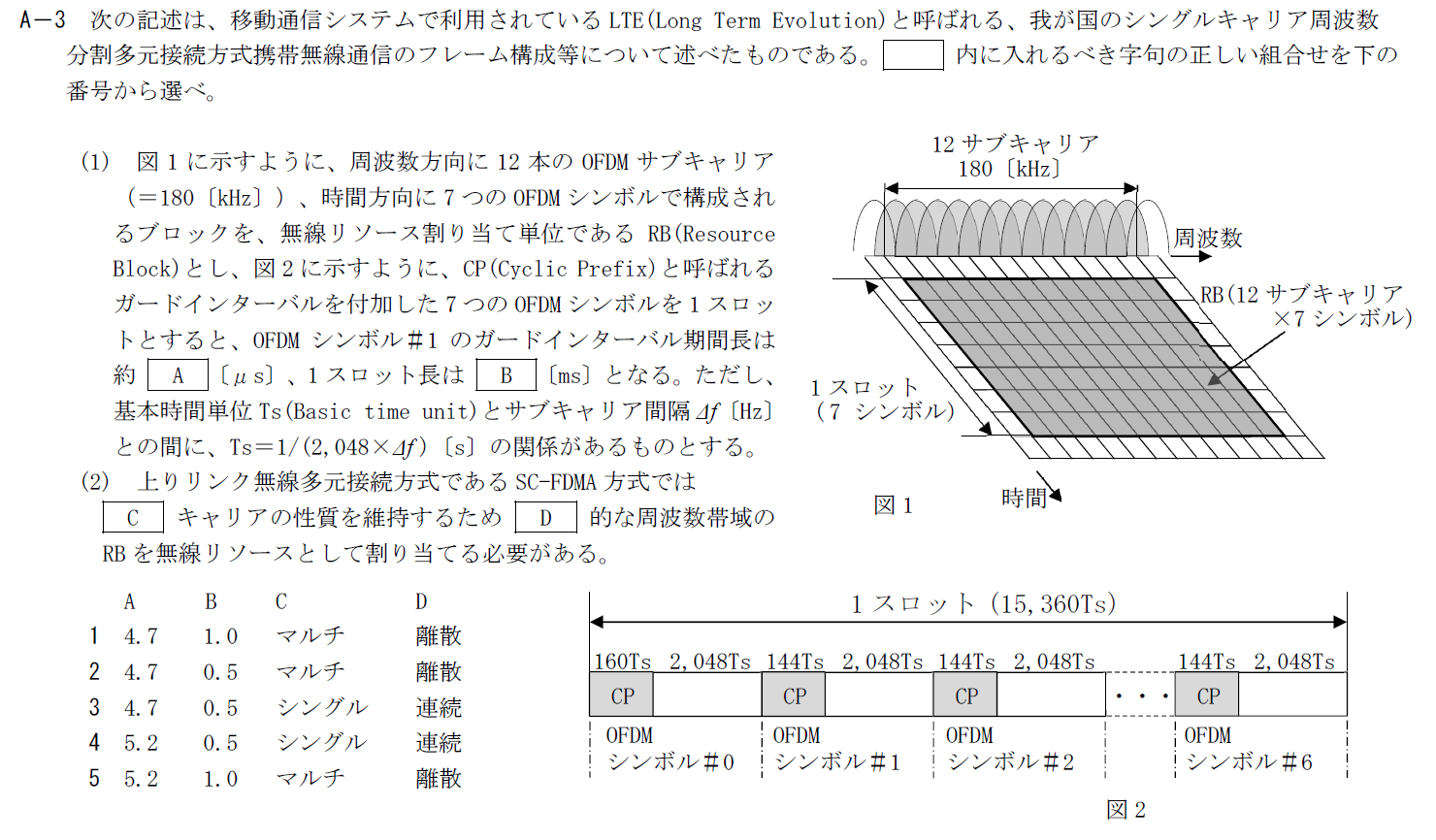
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-3
LTEのシングルキャリア周波数分割多元接続方式に関する問題です。
この問題は令和3年7月2回目A-1で類題が出題されています。
下記の記事もご参照ください。

A
基本時間単位は \[ T_s=1/(2048\times \Delta f)=32.55\rm{[ns]} \] です。
ガードインターバルは図2から \[ 144T_s=4.7\rm{[\mu s]} \] です。
そのため、Aには「$4.7\rm{[\mu s]}$」が入ります。
B
1スロットは$15360T_s$なので、 \[ 15360T_s=0.5\rm{[ms]} \] となります。
そのため、Bには「$0.5\rm{[ms]}$」が入ります。
C
SCはSingle Carrierの略なのでCには「シングル」が入ります。
D
シングルキャリアの性質を維持するためには連続したRB(Resource Block)を割り当てる必要があります。
そのため、Dには「連続」が入ります。
以上から答えは3です。
R.5.1 無線工学A(2回目) A-4
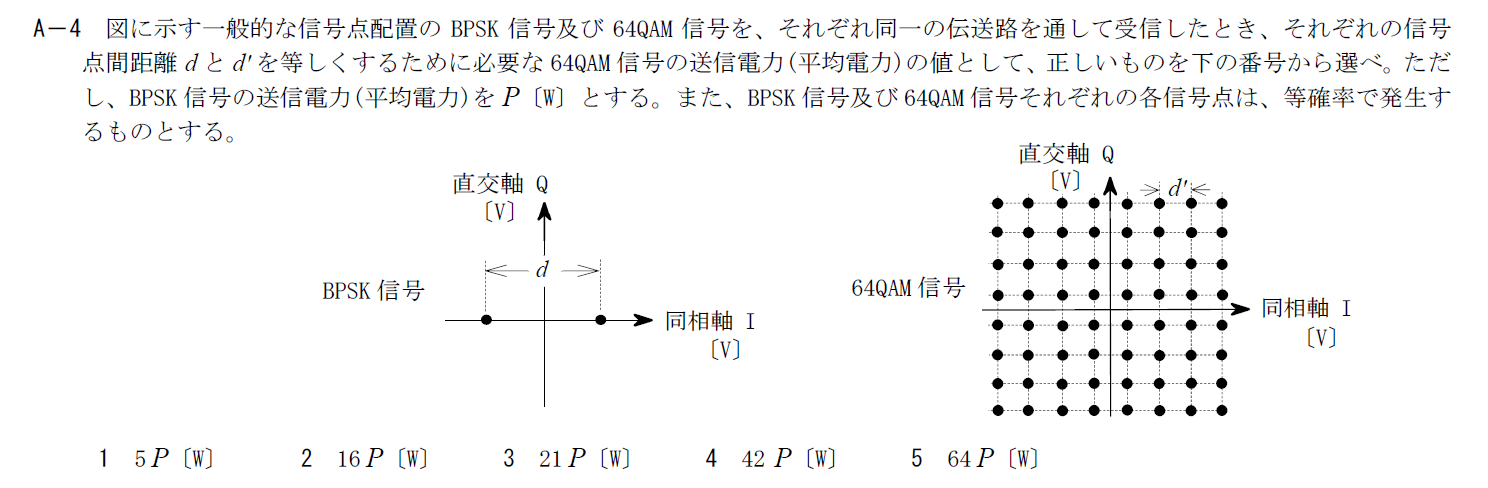
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-4
64QAMの信号点に関する問題です。
同様の問題で16QAMを扱った問題が令和4年7月2回目A-2で出題されています。
計算自体はこちらの問題の方が圧倒的に面倒くさいです。
基本的な計算については下記の記事をご参照ください。

BPSKについては上記の記事と同様で \[ P=\frac{d^2}{8} \] です。
次に64QAMの平均電力を求めます。平均電力なのですべての信号点の電力を足しあげて64で割る必要があります。 足しあげ方は自由ですが、第一象限だけ考えてそれを4倍する方法で計算します。
まず、点$(i,j)$の電力$P_{ij}$を考えてみましょう。
これはBPSKを考えた時と同様で、 \[ P_{ij}=\frac{1}{2}(i^2+j^2) \] です。 I成分とQ成分の2乗をそれぞれ足している格好となっています。
ここでは第一象限にある16点に対して、I成分の2乗を足しあげた$P_I$とQ成分の2乗を足しあげた$P_Q$を足して2で割ることにします。
I成分については$d’/2,3d’/2,5d’/2,7d’/2$の4つの値を持つ点がそれぞれ4つずつあります。 つまり \[ P_I=4\times \left\{\left(\frac{d’}{2}\right)^2+\left(\frac{3d’}{2}\right)^2+\left(\frac{5d’}{2}\right)^2+\left(\frac{7d’}{2}\right)^2\right\} \\ =84d’^2 \] Q成分についても同様です。
これらが4象限分あるので全電力$P_{all}$は \[ P_{all}=\frac{1}{2}(4P_I+4P_Q)=4\times 84d’^2 \] となり、平均電力$P_{64}$は \[ P_{64}=\frac{4\times 84d’^2}{64}=\frac{42}{8}d’^2 \] となります。
$d=d’$の時、$d’^2=8P$なので \[ P_{64}=42P \] となります。
以上から答えは4です。
R.5.1 無線工学A(2回目) A-5
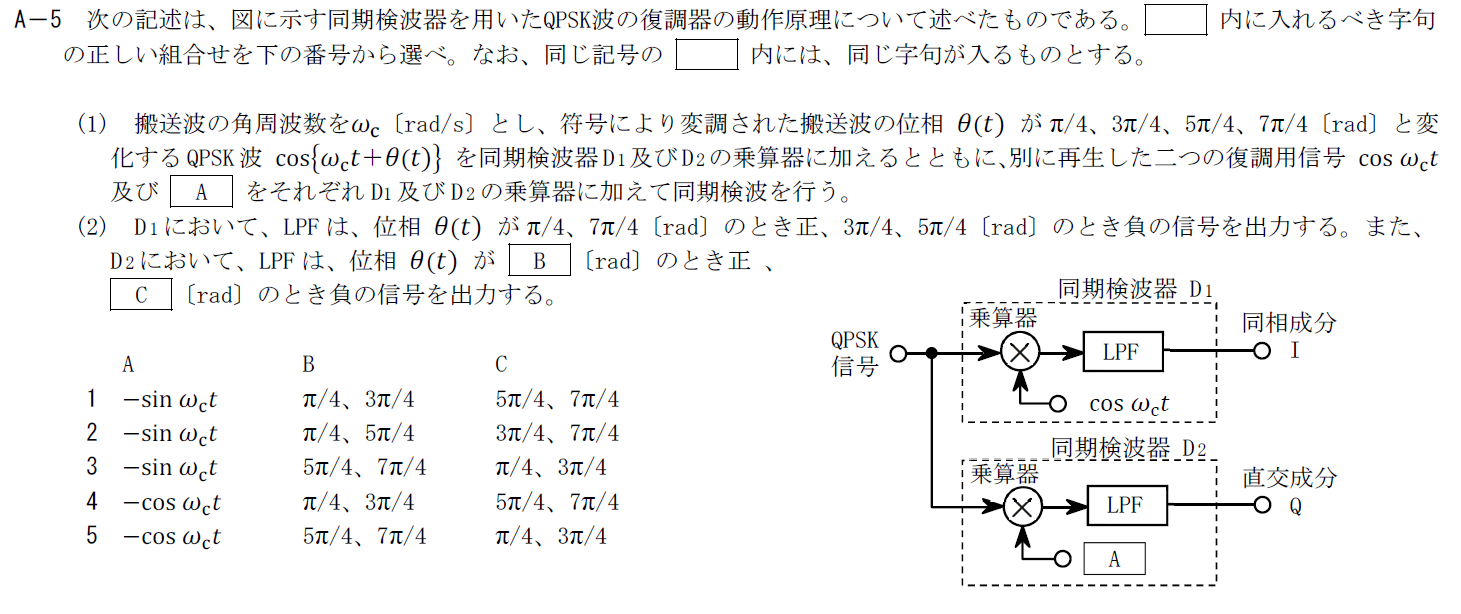
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月2回目 無線工学A A-5
同期検波を用いたQPSKの復調に関する問題です。
同様の問題が令和4年1月1回目A-5で出題されています。 (2)の部分が異なります。
A
同期検波器では互いに直交する信号をQPSK信号に乗算します。
$\cos \omega_ct$と直交する選択肢を探すと$-\sin \omega_ct$です。
そのため、Aには「$-\sin \omega_ct$」が入ります。
B,C
$D_2$でのLPFに入力される信号は \[ -\cos \{\omega_ct +\theta (t)\}\sin \omega_c t \\ =-\frac{1}{2}\sin \{2\omega_c t +\theta\}+\frac{1}{2}\sin \theta(t) \] となります。
LPFの出力の符号は$\sin \theta(t)$を考えればいいので、$\theta(t) =\frac{\pi}{4} , \frac{3}{4}\pi$の時は出力が正、$\theta(t) =\frac{5}{4}\pi , \frac{7}{4}\pi$の時は負の信号を出力します。
そのため、Bには「$\frac{\pi}{4} , \frac{3}{4}\pi$」、Cには「$\frac{5}{4}\pi , \frac{7}{4}\pi$」が入ります。
以上から答えは1です。
まとめ
今回は令和5年1月の無線工学A(2回目)の試験A-1~A-5の問題について解説しました。 A-4のような計算がとても面倒くさい問題も出題されています。計算ミスのリスクもあるので、後回しにすることも考えて問題を効率よくときましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント