【過去問解説】令和4年7月の1陸技試験問題を解いてみた（R4.7 2回目 無線工学B A-6~A-10）

令和4年7月の1陸技の試験2回目の無線工学BのA-6～10の問題について解説します。

R.4.7 無線工学B（2回目） A-6

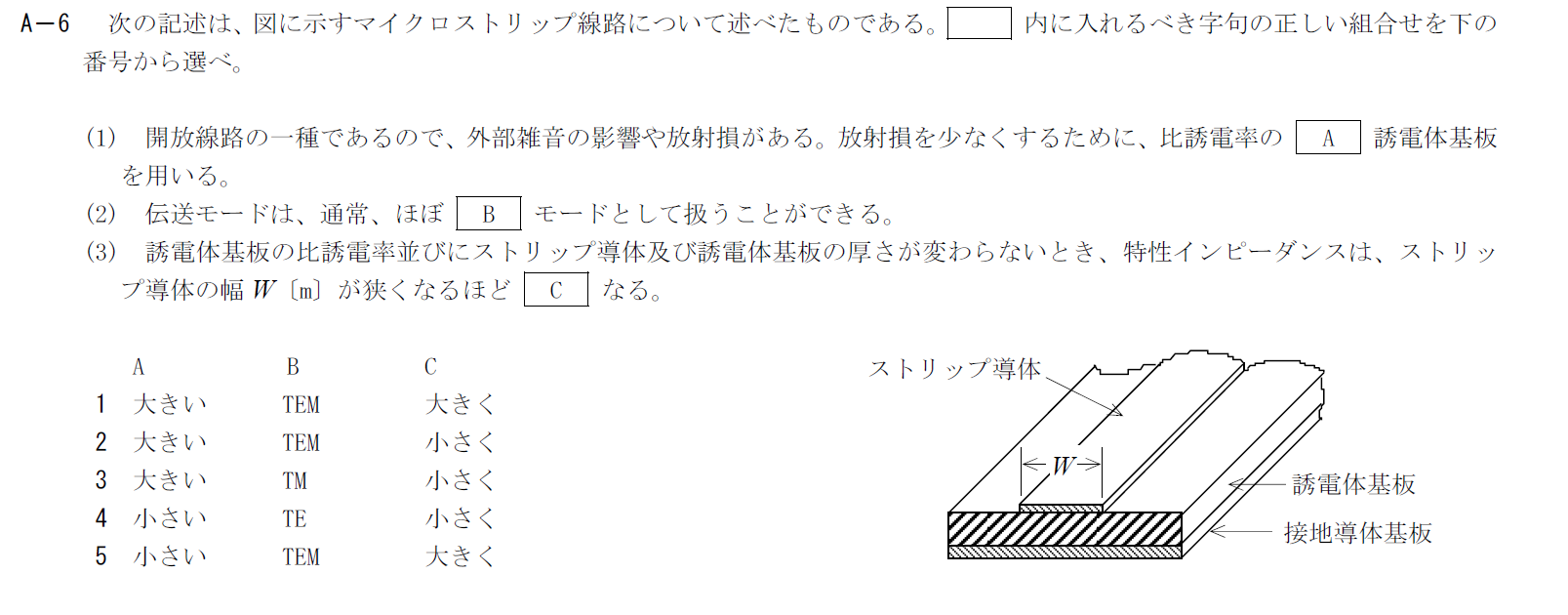
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年7月2回目　無線工学B A-6

マイクロストリップ線路に関する問題です。

この問題は類似問題が令和4年1月1回目の試験のB-3で出題されています。
こちらの方が詳細な問題となっているのでこちらも参考にしてください。

【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 無線工学B B-1~B-5）

１陸技令和4年1月の無線工学B(1回目)の問題を解いてみました。今回はB-1~5です。

jr2kcb.com

2022.02.26

A

マイクロストリップ線路の放射損を少なくするには静電容量を大きくする必要があるので比誘電率の大きい誘電体基板を使用します。

そのため、Aには「大きい」が入ります。

B

マイクロストリップ線路では電波はTEMモードで扱うことができます。

そのため、Bには「TEM」が入ります。

C

導体幅が狭くなるほど、静電容量は小さくなります。

特性インピーダンスは$Z_0=\sqrt{L/C}$で表されるので、$W$が小さくなるほどCが小さくなり、特性インピーダンスは大きくなります。

そのため、Cには「大きく」が入ります。

以上から答えは1です。

R.4.7 無線工学B（2回目） A-7

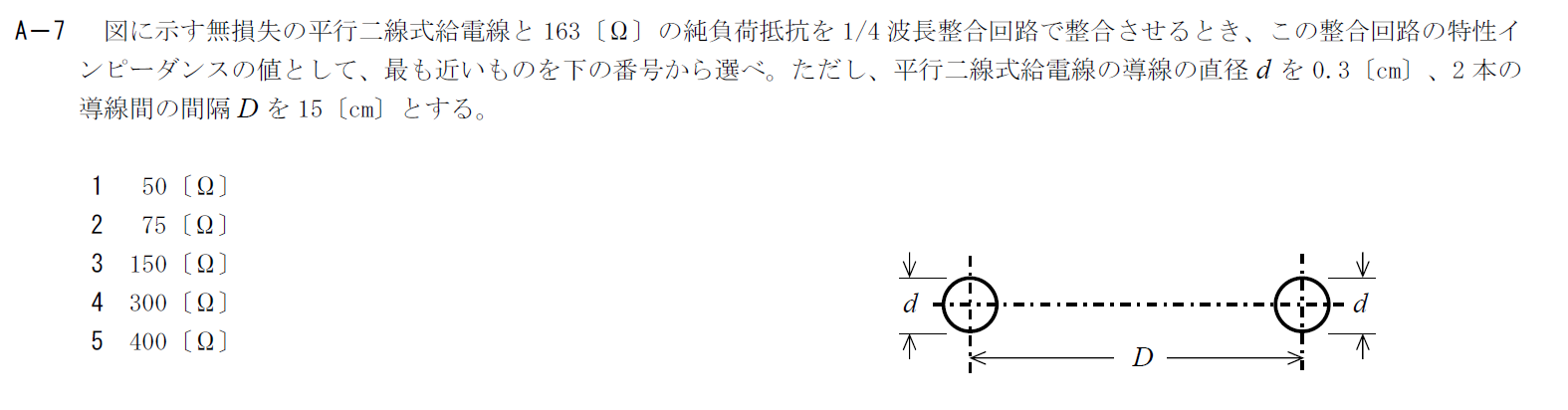
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年7月2回目　無線工学B A-7

平行二線式給電線の特性インピーダンス$Z_0$は$Z_0=276\log \frac{2D}{d}$で表せます。

負荷のインピーダンスを$Z_R$とすると、整合回路の特性インピーダンス$Z_Q$は
$$Z_Q=\sqrt{Z_0Z_R}$$
と表せます。

問題の値を代入すると
$$Z_Q=\sqrt{276\times \log\frac{2\times 15}{0.3}\times 163}=\sqrt{276\times 2\times 163} \\ ＝\sqrt{89976} \simeq 300$$
なので、答えは4.「300[$\rm{\Omega}$]」です。

試験では頑張って手計算するもの悪くないですが、問題の選択肢から近いものを選ぶので$276 \simeq 300, 2\times 163 \simeq 300$として答えを出してもよいでしょう。

R.4.7 無線工学B（2回目） A-8

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年7月2回目　無線工学B A-8

この問題はほぼ同じ内容の問題が令和3年1月1回目のB-2の問題で出ています。

【無線】1月の1陸技試験問題を解いてみた（R3.1 1回目　無線工学B B-1~B-5）

１陸技令和3年の無線工学Bの問題を解いてみました。今回は第2回B-1~5を解きました。

jr2kcb.com

2021.05.04

誤った選択肢は2です。
この選択肢は電界結合と磁界結合が逆転しています。

以上から答えは2です。

R.4.7 無線工学B（2回目） A-9

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年7月2回目　無線工学B A-9

給電線とアンテナが整合してないときの伝送効率に関する計算問題です。

A

減衰定数$a$の時、電圧が$\exp(-al)$に比例します。
電力は電圧の2乗に比例するので
$$\eta_0=P_R/P_T=\exp(-2al)$$
となります。

そのため、Aには「$-2al$」が入ります。

B

反射係数も減衰定数と同様で、電力は電圧の2乗に比例するので、
$$P_{\rm{RB}}=P_{\rm{RA}}|\Gamma|^2$$
となります。

そのため、Bには「$P_{\rm{RA}}|\Gamma|^2$」が入ります。

C

入力電力$P_{\rm{TA}}$を使って関係する変数を表す方針で計算します。

計算すると次のようになります。
$$P_{\rm{RA}}=\eta_0P_{\rm{TA}} \\ P_{\rm{RB}}=\eta_0|\Gamma|^2P_{\rm{TA}} \\ P_{\rm{TB}}=\eta_0P_{\rm{RB}}=\eta_0^2|\Gamma|^2P_{\rm{TA}}$$

①の式に代入すると
$$\eta =\frac{\eta_0P_{\rm{TA}}-\eta_0|\Gamma|^2P_{\rm{TA}}}{P_{\rm{TA}}-\eta_0^2|\Gamma|^2P_{\rm{TA}}} \\ =\eta_0\frac{1-|\Gamma|^2}{1-|\Gamma|^2\eta_0^2}$$
となります。

そのため、Cには「$\eta_0\frac{1-|\Gamma|^2}{1-|\Gamma|^2\eta_0^2}$」が入ります。

以上から答えは5です。

R.4.7 無線工学B（2回目） A-10

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R4年7月2回目　無線工学B A-10

延長コイルの定数を計算する問題です。

まず波長を計算しておきましょう。
$$\lambda =100[\rm{m}]$$

長さlのアンテナのインピーダンス$Z_l$は
$$Z_l=-jZ_0\cot \frac{2\pi}{\lambda}l$$
なので、問題の値を代入すると
$$Z_l=-j628\cot \frac{2\pi}{100}\times 12.5 \\ =-j628\cot \frac{\pi}{4}=-j628$$
です。

延長コイルを挿入したとき共振するということはインピーダンスの虚部がゼロとなることを意味します。
上記を打ち消すようなインダクタンスを求めましょう。

延長コイルのインダクタンスを$L$とすると、
$$2\pi fL=628 \\ L=\frac{628}{2\pi \times 3 \times 10^6} \\ =33.3 \times 10^{-6}[\rm{H}]=33.3[\rm{\mu H}]$$
となります。

以上から答えは1です。

まとめ

今回は令和4年7月の無線工学B(2回目)の試験A6~A-10の問題について解説しました。
1陸技の試験では必ずと言っていいほど導波管や線路に関する問題が出題されます。
暗記しようとすると係数が中途半端なものも多いので面倒かもしれませんが、すぐに導くのも難しいので覚えておくのが無難でしょう。
138やその倍の276が多く登場するのでその値だけでも覚えておくと結果が変わるかもしれません。
この値は空間の特性インピーダンス$120\pi$と関連して出てくるものです。

試験の申し込み始まりましたね。受験される方は忘れないうちに申し込んでおきましょう。

勉強法

第一級陸上無線技術士の勉強法とおすすめ参考書

参考文献

電磁気学をちゃんと学びたい人向け

上の難易度が高い人